冀教版九年级数学下册29.1点与圆的位置关系课件(24张ppt)
文档属性
| 名称 | 冀教版九年级数学下册29.1点与圆的位置关系课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 15:53:14 | ||
图片预览




文档简介
(共24张PPT)
29.1
点与圆的位置关系
第二十九章
直线与圆的位置关系
冀教版九下
1.理解并掌握点和圆的三种位置关系.
2.会用用图形表示点和圆的位置关系.
3.会用数量表示点和圆的位置关系.
学
习
目
标
创设问题情境,引入新课
实际问题:石家庄某建筑物爆破时所产生的冲击波,对其周围半径为300米的圆形区域都有影响.超市A、B、C与爆破中心的距离分别是250米、300米、360米.则哪所超市会受到爆破的影响,应该采取相应的措施?
超市A、超市B会受到影响,应采取相应的措施.
超市C不会受到影响,不必采取措施.
创设问题情境,引入新课
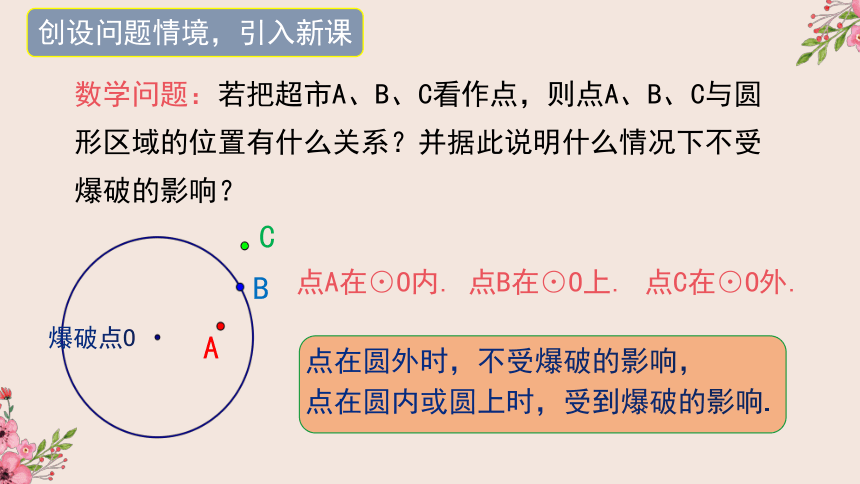
数学问题:若把超市A、B、C看作点,则点A、B、C与圆形区域的位置有什么关系?并据此说明什么情况下不受爆破的影响?
点A在⊙O内.
A
B
C
爆破点O
点B在⊙O上.
点C在⊙O外.
点在圆外时,不受爆破的影响,
点在圆内或圆上时,受到爆破的影响.
一起探究
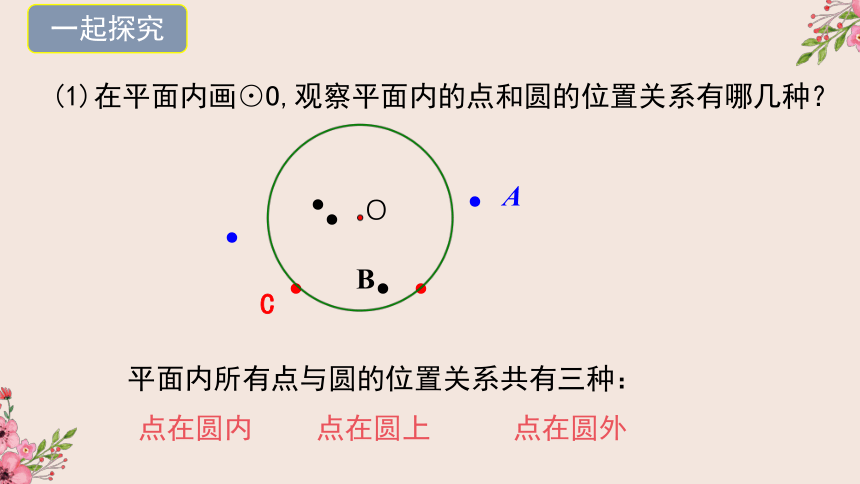
(1)在平面内画⊙O,观察平面内的点和圆的位置关系有哪几种?
.
C
.
.
.
B
.
.A
.
平面内所有点与圆的位置关系共有三种:
点在圆内
点在圆上
点在圆外
O
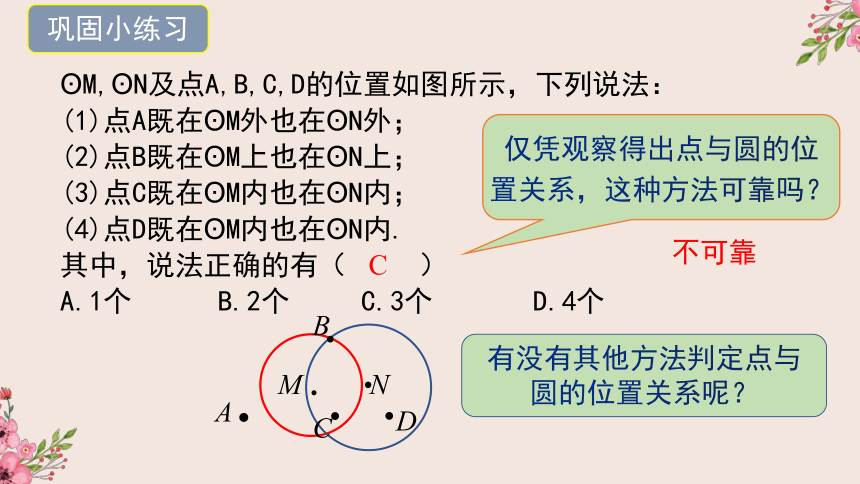
?M,?N及点A,B,C,D的位置如图所示,下列说法:
(1)点A既在?M外也在?N外;
(2)点B既在?M上也在?N上;
(3)点C既在?M内也在?N内;
(4)点D既在?M内也在?N内.
其中,说法正确的有(
)
A.1个
B.2个
C.3个
D.4个
D
N
M
C
B
C
A
巩固小练习
仅凭观察得出点与圆的位置关系,这种方法可靠吗?
不可靠
有没有其他方法判定点与圆的位置关系呢?
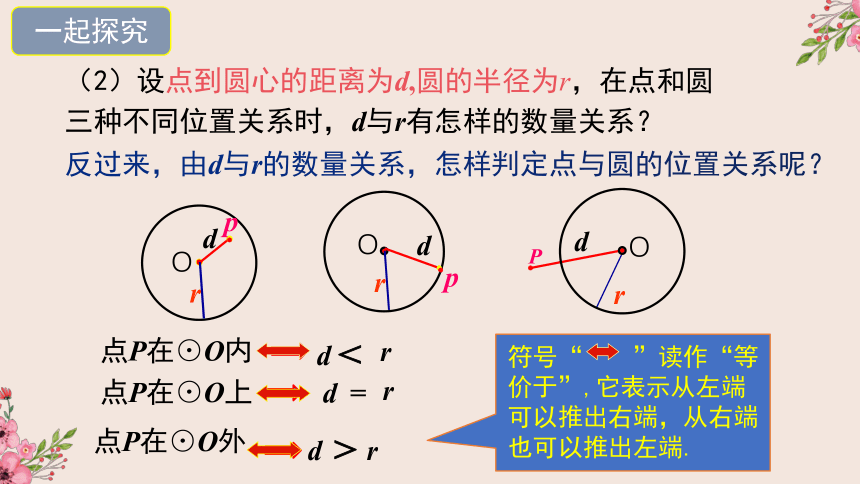
(2)设点到圆心的距离为d,圆的半径为r,在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
p
d
p
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
符号“
”读作“等
价于”,它表示从左端
可以推出右端,从右端
也可以推出左端.
一起探究
O
O
O
归纳总结
r
p
d
p
r
d
P
r
d
R
r
P
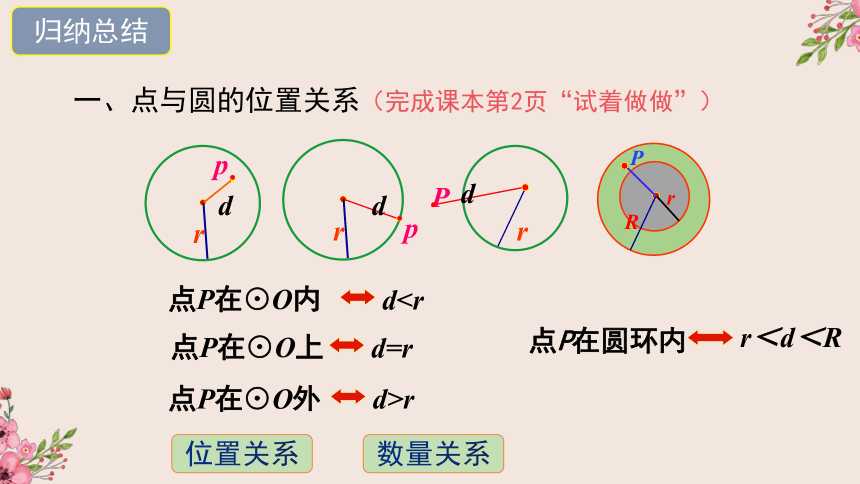
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r<d<R
一、点与圆的位置关系(完成课本第2页“试着做做”)
位置关系
数量关系
归纳总结
二、解读
d:点到圆心的距离
r:圆的半径
要判断一个点和一个圆的位置关系,要先确定问题中的d和r,通过d和r的大小比较,得出点与圆的位置关系.
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
.
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP=
,则点P在(
)
A.在大圆内
B.在小圆内
C.小圆外
D.大圆内,小圆外
o
D
巩固小练习
例1
(课本第3页例题)如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:(1)
典例精析
d=AC=3cm,r=3cm
∴d=r
∴点C在⊙A上.
例1
(课本第3页例题)如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:(2)∵d=AB=5cm,r=3cm
典例精析
r=3cm
∴d>r
∴点B在⊙A外.
(3)
∴d<r
∴点D在⊙A内.
例1
.(变式)如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,CE⊥AB于点E,以点C为圆心、3cm为半径画圆,判断点E与⊙C的位置关系.
●
B
A
E
C
典例精析
∴d=CE=2.4cm,r=3cm
(4)
∴d<r
∴点E在⊙C内.
求CE的长度,还可以用什么方法?
相似
三角函数
关键:确定d与r
典例精析
例2.如图,已知⊙O的半径为6cm,点P到圆心O的距离为10cm,点M为⊙O上一动点,求PM的最小值及最大值.
O
P
典例精析
如图,连接PO交⊙O于点A,以PA为半径做⊙P时,点A在⊙P上,⊙O上的其他点都在⊙P外,因此点P与⊙O上的点所连的线段中,PA是最短的。
解析:
P
O
A
典例精析
如图,连接PO,并延长与⊙O相交与点B.以PB为半径做⊙P,点B在⊙P上,⊙O上的其他点都在⊙P内,因此点P与⊙O上的点所连的线段中,PB是最长的。
P
O
B
解析:
典例精析
例2.如图,已知⊙O的半径为6cm,点P到圆心O的距离为10cm,点M为⊙O上一动点,求PM的最小值及最大值.
O
P
●
●
A
B
解:连接PO,交⊙O于点A,延长PO交⊙O于点B.
当点M运动到点A时,PM最小,此时PM=10-6=4cm.
当点P运动到点B时,PM最大,
此时PM=10+6=16cm.
典例精析
例2.(拓展)如图,已知P是⊙O外一定点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,求线段OM的最小值.
O
P
Q
M
A
B
分析:设OP与⊙O交于点A
由OP=4,OA=2,
可得点A为OP的中点
因此可知AM是△POQ的中位线
则AM的长度为定值1
即点M在以点A为圆心、1为半径的圆上.(转化为例2)
典例精析
例2.(拓展)如图,已知P是⊙O外一定点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,求线段OM的最小值.
O
P
Q
M
A
B
解:设OP与⊙O交于点A,连接AM,以点A为圆心、AM为半径作圆
∵OP=4,OA=2
∴点A为OP的中点,又M为PQ的中点
∴AM=
OQ=1
∴点M在⊙上
设OP与⊙A交于点B,则点M远动到点B时,OM最小,OM=2-1=1.
1.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
;点D在⊙A
.
上
外
上
2.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为
(
)
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.在⊙O上或⊙O外
B
课堂小测
3.在Rt△ABC中,∠A=30°,∠C=90°,BC=2,以点A为圆心r为半径画圆,使点C在⊙A内而点B在⊙A外,则r的取值范围为
.
解析:利用锐角三角函数与勾股定理,求得AB=4,AC=
,则r的取值范围为AC<r<AB,即
.
课堂小测
课堂小测
4.如图,⊙O的半径为5,圆心O到弦AB的距离为2.⊙O上到弦AB所在直线的距离为2的点有几个?
O
B
A
●
●
●
●
2
2
答案:4个
A
B
O
3
2
●
●
2
●
答案:3个
想一想:设圆心O到弦AB的距离为d,当⊙O上到弦AB所在直线的距离为2的点有2个时,d的取值范围是什么?
3<d<5
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
课堂小结
同学们再见
29.1
点与圆的位置关系
第二十九章
直线与圆的位置关系
冀教版九下
1.理解并掌握点和圆的三种位置关系.
2.会用用图形表示点和圆的位置关系.
3.会用数量表示点和圆的位置关系.
学
习
目
标
创设问题情境,引入新课
实际问题:石家庄某建筑物爆破时所产生的冲击波,对其周围半径为300米的圆形区域都有影响.超市A、B、C与爆破中心的距离分别是250米、300米、360米.则哪所超市会受到爆破的影响,应该采取相应的措施?
超市A、超市B会受到影响,应采取相应的措施.
超市C不会受到影响,不必采取措施.
创设问题情境,引入新课
数学问题:若把超市A、B、C看作点,则点A、B、C与圆形区域的位置有什么关系?并据此说明什么情况下不受爆破的影响?
点A在⊙O内.
A
B
C
爆破点O
点B在⊙O上.
点C在⊙O外.
点在圆外时,不受爆破的影响,
点在圆内或圆上时,受到爆破的影响.
一起探究
(1)在平面内画⊙O,观察平面内的点和圆的位置关系有哪几种?
.
C
.
.
.
B
.
.A
.
平面内所有点与圆的位置关系共有三种:
点在圆内
点在圆上
点在圆外
O
?M,?N及点A,B,C,D的位置如图所示,下列说法:
(1)点A既在?M外也在?N外;
(2)点B既在?M上也在?N上;
(3)点C既在?M内也在?N内;
(4)点D既在?M内也在?N内.
其中,说法正确的有(
)
A.1个
B.2个
C.3个
D.4个
D
N
M
C
B
C
A
巩固小练习
仅凭观察得出点与圆的位置关系,这种方法可靠吗?
不可靠
有没有其他方法判定点与圆的位置关系呢?
(2)设点到圆心的距离为d,圆的半径为r,在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
p
d
p
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
符号“
”读作“等
价于”,它表示从左端
可以推出右端,从右端
也可以推出左端.
一起探究
O
O
O
归纳总结
r
p
d
p
r
d
P
r
d
R
r
P
点P在⊙O内
d
d=r
点P在⊙O外
d>r
点P在圆环内
r<d<R
一、点与圆的位置关系(完成课本第2页“试着做做”)
位置关系
数量关系
归纳总结
二、解读
d:点到圆心的距离
r:圆的半径
要判断一个点和一个圆的位置关系,要先确定问题中的d和r,通过d和r的大小比较,得出点与圆的位置关系.
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
.
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP=
,则点P在(
)
A.在大圆内
B.在小圆内
C.小圆外
D.大圆内,小圆外
o
D
巩固小练习
例1
(课本第3页例题)如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:(1)
典例精析
d=AC=3cm,r=3cm
∴d=r
∴点C在⊙A上.
例1
(课本第3页例题)如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:(2)∵d=AB=5cm,r=3cm
典例精析
r=3cm
∴d>r
∴点B在⊙A外.
(3)
∴d<r
∴点D在⊙A内.
例1
.(变式)如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,CE⊥AB于点E,以点C为圆心、3cm为半径画圆,判断点E与⊙C的位置关系.
●
B
A
E
C
典例精析
∴d=CE=2.4cm,r=3cm
(4)
∴d<r
∴点E在⊙C内.
求CE的长度,还可以用什么方法?
相似
三角函数
关键:确定d与r
典例精析
例2.如图,已知⊙O的半径为6cm,点P到圆心O的距离为10cm,点M为⊙O上一动点,求PM的最小值及最大值.
O
P
典例精析
如图,连接PO交⊙O于点A,以PA为半径做⊙P时,点A在⊙P上,⊙O上的其他点都在⊙P外,因此点P与⊙O上的点所连的线段中,PA是最短的。
解析:
P
O
A
典例精析
如图,连接PO,并延长与⊙O相交与点B.以PB为半径做⊙P,点B在⊙P上,⊙O上的其他点都在⊙P内,因此点P与⊙O上的点所连的线段中,PB是最长的。
P
O
B
解析:
典例精析
例2.如图,已知⊙O的半径为6cm,点P到圆心O的距离为10cm,点M为⊙O上一动点,求PM的最小值及最大值.
O
P
●
●
A
B
解:连接PO,交⊙O于点A,延长PO交⊙O于点B.
当点M运动到点A时,PM最小,此时PM=10-6=4cm.
当点P运动到点B时,PM最大,
此时PM=10+6=16cm.
典例精析
例2.(拓展)如图,已知P是⊙O外一定点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,求线段OM的最小值.
O
P
Q
M
A
B
分析:设OP与⊙O交于点A
由OP=4,OA=2,
可得点A为OP的中点
因此可知AM是△POQ的中位线
则AM的长度为定值1
即点M在以点A为圆心、1为半径的圆上.(转化为例2)
典例精析
例2.(拓展)如图,已知P是⊙O外一定点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,求线段OM的最小值.
O
P
Q
M
A
B
解:设OP与⊙O交于点A,连接AM,以点A为圆心、AM为半径作圆
∵OP=4,OA=2
∴点A为OP的中点,又M为PQ的中点
∴AM=
OQ=1
∴点M在⊙上
设OP与⊙A交于点B,则点M远动到点B时,OM最小,OM=2-1=1.
1.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
;点D在⊙A
.
上
外
上
2.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为
(
)
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.在⊙O上或⊙O外
B
课堂小测
3.在Rt△ABC中,∠A=30°,∠C=90°,BC=2,以点A为圆心r为半径画圆,使点C在⊙A内而点B在⊙A外,则r的取值范围为
.
解析:利用锐角三角函数与勾股定理,求得AB=4,AC=
,则r的取值范围为AC<r<AB,即
.
课堂小测
课堂小测
4.如图,⊙O的半径为5,圆心O到弦AB的距离为2.⊙O上到弦AB所在直线的距离为2的点有几个?
O
B
A
●
●
●
●
2
2
答案:4个
A
B
O
3
2
●
●
2
●
答案:3个
想一想:设圆心O到弦AB的距离为d,当⊙O上到弦AB所在直线的距离为2的点有2个时,d的取值范围是什么?
3<d<5
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
课堂小结
同学们再见
