北师大版九年级数学上册 第六章反比例函数复习课件(19张)
文档属性
| 名称 | 北师大版九年级数学上册 第六章反比例函数复习课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 734.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 18:18:50 | ||
图片预览





文档简介
(共19张PPT)
反比例函数复习课
?
复习目标:
?
?
(1)巩固反比例函数的概念,会求反比例函数表达式并能画出图象.
?(2)巩固反比例函数图象的变化其及性质并能运用解决某些实际问题.
复习重点、难点:
重点:反比例函数的定义、图像性质。???
难点:反比例函数增减性的理解。
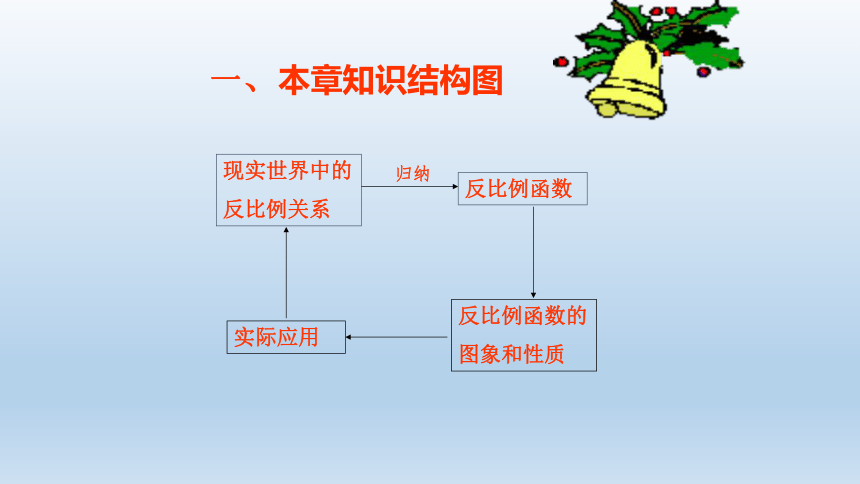
一、本章知识结构图
现实世界中的
反比例关系
反比例函数
实际应用
反比例函数的
图象和性质
归纳
二
重点知识
三、考点整合训练
考点1:反比例函数的概念
1.函数
是
函数,其图象为
,其中
k=
,自变量x的取值范围为
.
反比例
双曲线
2
x≠
0
2.若
为反比例函数,则m=__.
2
若
为反比例函数,则m=
__
-1
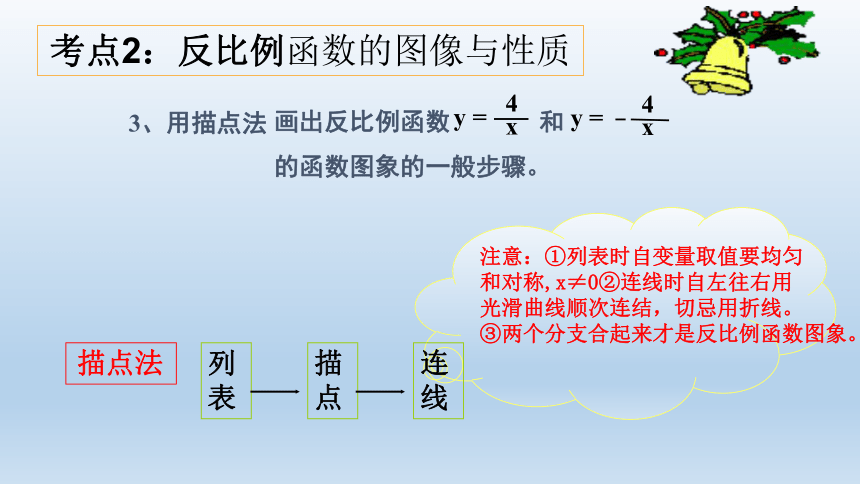
画出反比例函数
和
的函数图象的一般步骤。
y
=
x
4
y
=
x
4
注意:①列表时自变量取值要均匀
和对称,x≠0②连线时自左往右用
光滑曲线顺次连结,切忌用折线。
③两个分支合起来才是反比例函数图象。
考点2:反比例函数的图像与性质
列
表
描
点
连
线
描点法
3、用描点法
考点2:反比例函数的图像与性质
4.函数
的图象位于第
象限,
在每一象限内,y的值随x的增大而
,
当x>0时,y
0,这部分图象位于第
象限.
一、三
减小
>
一
考点2:反比例函数的图像与性质
5.如果反比例函数
的图象位于第二、四象限,那么m的范围为
.
由1-3m<0
得-3m<-
1
m>
m>
∴
6.已知点A(-2,y1),B(-1,y2),C
(4,y3)
都在反比例函数
的图象上,则y1、y2与y3的大小关系(从大到小)为
.
y
x
o
-1
y2
A
B
-2
4
C
y3
y3
>y1>y2
方法1
用图像法解
下下
y1
方法2
用求值法解
∵当x1=-2时,
y1=-2
当x2=-1
时,y2=-4
当x3=4时
,y3=1
∴
y3>
y1
>y2
考点3:反比例函数与正比例函数
的关系
函数
正比例函数
反比例函数
表达式
图象
及象限
性质
在每一个象限内:
当k>0时,y随x的增大而减小;
当k<0时,y随x的增大而增大.
y=kx(k≠0)(
特殊的一次函数)
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
k<0
x
y
o
x
y
o
k>0
k<0
y
x
0
y
0
k>0
x
7.已知函数y=k/x
的图象如下右图,则y=k
x-2
的图象大致是( )
x
x
x
x
x
y
y
y
y
y
o
o
o
o
o
(A)
(D)
(C)
(B)
D
8.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是
.
x
y
o
M
N
p
考点4:反比例函数的几何意义
(变式练习)一个反比例函数的图象在第二象限,如图,点A是图象上任意一点,AM⊥x轴于点M,O是原点,如果△AOM的面积为3,则这个反比例函数的解析式是
。
x
y
o
M
A
y=-6/x
9。已知反比例函数y
=k/x
和一次函数
y=kx+b的图象都经过点(2,1)
(1)分别求出这个函数的解析式
考点5:反比例函数与一次函数的综合运用
解:(1)∵反比例函数y=k/x的图像经过点(2,1)
∴1=k/2,即k=2
∴反比例函数的解析式为y=2/x
又∵一次函数y=kx+b和反比例函数y=k/x的k值相等,
且也经过点(2,1)
解得k=2,b=-3
∴一次函数的解析式为y=2x
-3
K=2
1=2×2+b
∴
解:(2)当x=
-2时,反比例函数的函数值y=
-1;一次函数的函数值y=
-7
∴点A(
-2,-1)在反比例函数的图像上。
小结
(2)试判断是A(-2,
-1)在哪个函数的图象上
课堂小结:
请大家围绕以下几个问题小结本课内容:
1、反比例函数的图象是什么样子的?
它与正比例函数的图象有什么不同?
2、反比例函数的性质是什么?
它与正比例函数有什么共同点和不同点?
3、在本节课练习中你运用了哪些数学思想和方法?
1、函数
的图象在第________象限,
在每一象限内,y
随x
的增大而_________.
2、函数
的图象在第________象限,
在每一象限内,y
随x
的增大而_________.
3、函数
,当x>0时,图象在第____象限,
y随x
的增大而_________.
填一填
我能行!!!
一
三
减小
二
四
增大
一
减小
如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( ).
A、x<-1
B、x>2
C、-1<x<0或x>2 D、x<-1或0<x<2
D
做一做
1、如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,A点的坐标为(
,0),
OA=OB=AC.
(1)求一次函数的解析式
(2)求反比例函数的解析式
(3)求点D的坐标(两图像交点与原点围成的三角形面积)
A
B
C
D
O
x
y
课后思考与
探
究
反比例函数复习课
?
复习目标:
?
?
(1)巩固反比例函数的概念,会求反比例函数表达式并能画出图象.
?(2)巩固反比例函数图象的变化其及性质并能运用解决某些实际问题.
复习重点、难点:
重点:反比例函数的定义、图像性质。???
难点:反比例函数增减性的理解。
一、本章知识结构图
现实世界中的
反比例关系
反比例函数
实际应用
反比例函数的
图象和性质
归纳
二
重点知识
三、考点整合训练
考点1:反比例函数的概念
1.函数
是
函数,其图象为
,其中
k=
,自变量x的取值范围为
.
反比例
双曲线
2
x≠
0
2.若
为反比例函数,则m=__.
2
若
为反比例函数,则m=
__
-1
画出反比例函数
和
的函数图象的一般步骤。
y
=
x
4
y
=
x
4
注意:①列表时自变量取值要均匀
和对称,x≠0②连线时自左往右用
光滑曲线顺次连结,切忌用折线。
③两个分支合起来才是反比例函数图象。
考点2:反比例函数的图像与性质
列
表
描
点
连
线
描点法
3、用描点法
考点2:反比例函数的图像与性质
4.函数
的图象位于第
象限,
在每一象限内,y的值随x的增大而
,
当x>0时,y
0,这部分图象位于第
象限.
一、三
减小
>
一
考点2:反比例函数的图像与性质
5.如果反比例函数
的图象位于第二、四象限,那么m的范围为
.
由1-3m<0
得-3m<-
1
m>
m>
∴
6.已知点A(-2,y1),B(-1,y2),C
(4,y3)
都在反比例函数
的图象上,则y1、y2与y3的大小关系(从大到小)为
.
y
x
o
-1
y2
A
B
-2
4
C
y3
y3
>y1>y2
方法1
用图像法解
下下
y1
方法2
用求值法解
∵当x1=-2时,
y1=-2
当x2=-1
时,y2=-4
当x3=4时
,y3=1
∴
y3>
y1
>y2
考点3:反比例函数与正比例函数
的关系
函数
正比例函数
反比例函数
表达式
图象
及象限
性质
在每一个象限内:
当k>0时,y随x的增大而减小;
当k<0时,y随x的增大而增大.
y=kx(k≠0)(
特殊的一次函数)
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
k<0
x
y
o
x
y
o
k>0
k<0
y
x
0
y
0
k>0
x
7.已知函数y=k/x
的图象如下右图,则y=k
x-2
的图象大致是( )
x
x
x
x
x
y
y
y
y
y
o
o
o
o
o
(A)
(D)
(C)
(B)
D
8.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是
.
x
y
o
M
N
p
考点4:反比例函数的几何意义
(变式练习)一个反比例函数的图象在第二象限,如图,点A是图象上任意一点,AM⊥x轴于点M,O是原点,如果△AOM的面积为3,则这个反比例函数的解析式是
。
x
y
o
M
A
y=-6/x
9。已知反比例函数y
=k/x
和一次函数
y=kx+b的图象都经过点(2,1)
(1)分别求出这个函数的解析式
考点5:反比例函数与一次函数的综合运用
解:(1)∵反比例函数y=k/x的图像经过点(2,1)
∴1=k/2,即k=2
∴反比例函数的解析式为y=2/x
又∵一次函数y=kx+b和反比例函数y=k/x的k值相等,
且也经过点(2,1)
解得k=2,b=-3
∴一次函数的解析式为y=2x
-3
K=2
1=2×2+b
∴
解:(2)当x=
-2时,反比例函数的函数值y=
-1;一次函数的函数值y=
-7
∴点A(
-2,-1)在反比例函数的图像上。
小结
(2)试判断是A(-2,
-1)在哪个函数的图象上
课堂小结:
请大家围绕以下几个问题小结本课内容:
1、反比例函数的图象是什么样子的?
它与正比例函数的图象有什么不同?
2、反比例函数的性质是什么?
它与正比例函数有什么共同点和不同点?
3、在本节课练习中你运用了哪些数学思想和方法?
1、函数
的图象在第________象限,
在每一象限内,y
随x
的增大而_________.
2、函数
的图象在第________象限,
在每一象限内,y
随x
的增大而_________.
3、函数
,当x>0时,图象在第____象限,
y随x
的增大而_________.
填一填
我能行!!!
一
三
减小
二
四
增大
一
减小
如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( ).
A、x<-1
B、x>2
C、-1<x<0或x>2 D、x<-1或0<x<2
D
做一做
1、如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,A点的坐标为(
,0),
OA=OB=AC.
(1)求一次函数的解析式
(2)求反比例函数的解析式
(3)求点D的坐标(两图像交点与原点围成的三角形面积)
A
B
C
D
O
x
y
课后思考与
探
究
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
