沪科版(2012)初中数学八年级上册15.2 线段的垂直平分线 性质及其应用 课件(13张)
文档属性
| 名称 | 沪科版(2012)初中数学八年级上册15.2 线段的垂直平分线 性质及其应用 课件(13张) | 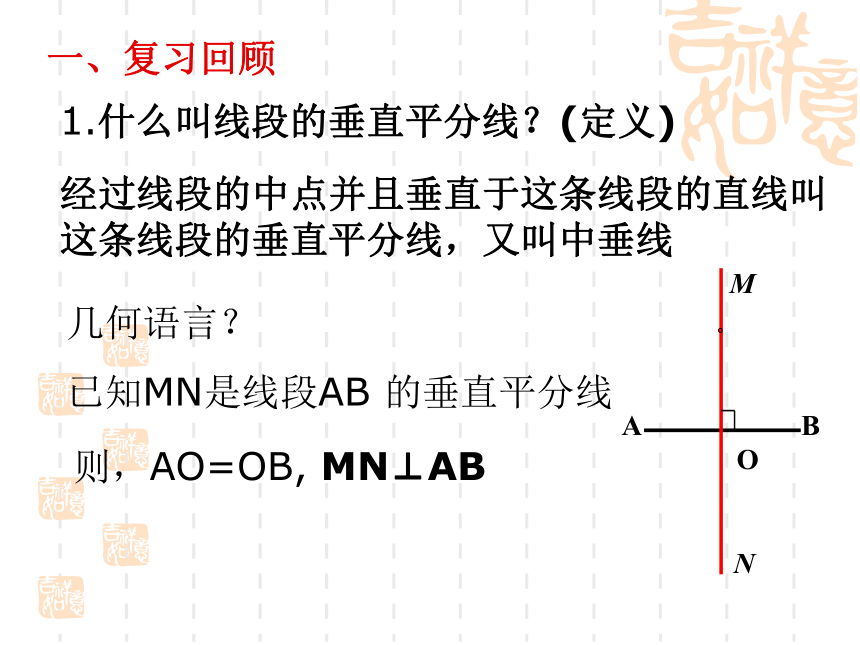 | |
| 格式 | zip | ||
| 文件大小 | 139.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 18:18:55 | ||
图片预览



文档简介
(共13张PPT)
一、复习回顾
1.什么叫线段的垂直平分线?(定义)
经过线段的中点并且垂直于这条线段的直线叫这条线段的垂直平分线,又叫中垂线
A
B
O
M
N
几何语言?
已知MN是线段AB
的垂直平分线
则,AO=OB,
MN⊥AB
线段垂直平分线
性质及其应用
15.2
线段的垂直平分线
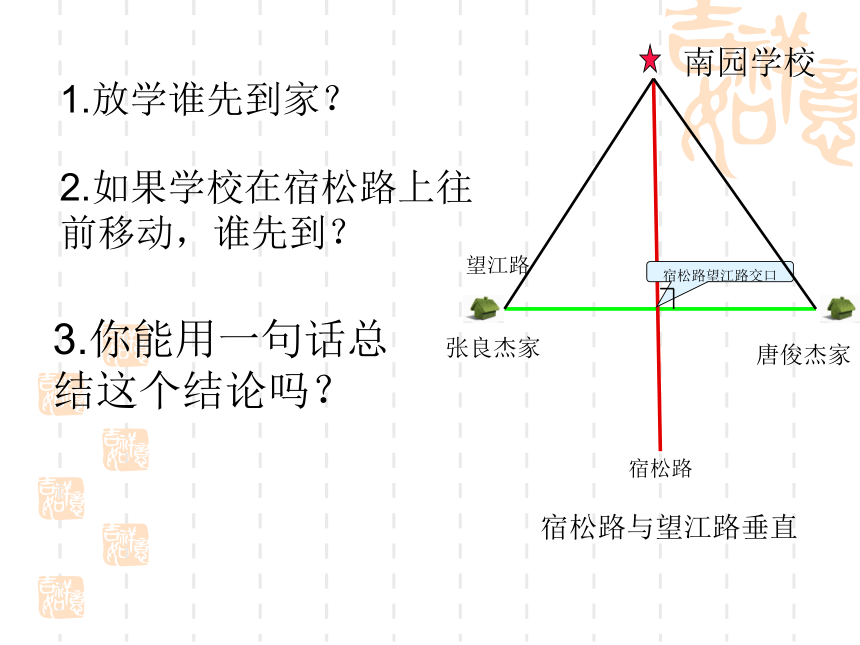
合肥市南园学校八二班“三杰”的对话:
一天,我班唐俊杰与张良杰同时从家出发到学校,二人约定走路速度一样,结果巧合的是二人同时到达望江路宿松路交口,(望江路宿松路可以看成是垂直的)然后他们沿宿松路一起到了学校,但在教室内发生了如此的对话:
张良杰:如果不考虑我们两家到学校间的建筑物,从学校各修一条路直达我们两人家,我们还是同时同速的话,放学我就比你先到家;
唐俊杰:不对,应该我先到。
为此,二人争论不休,就在这时,李邵杰插了一句:“别吵了,你们同时到。”
张良杰家
唐俊杰家
宿松路望江路交口
宿松路
望江路
南园学校
宿松路与望江路垂直
1.放学谁先到家?
2.如果学校在宿松路上往
前移动,谁先到?
3.你能用一句话总结这个结论吗?
A
B
P
M
N
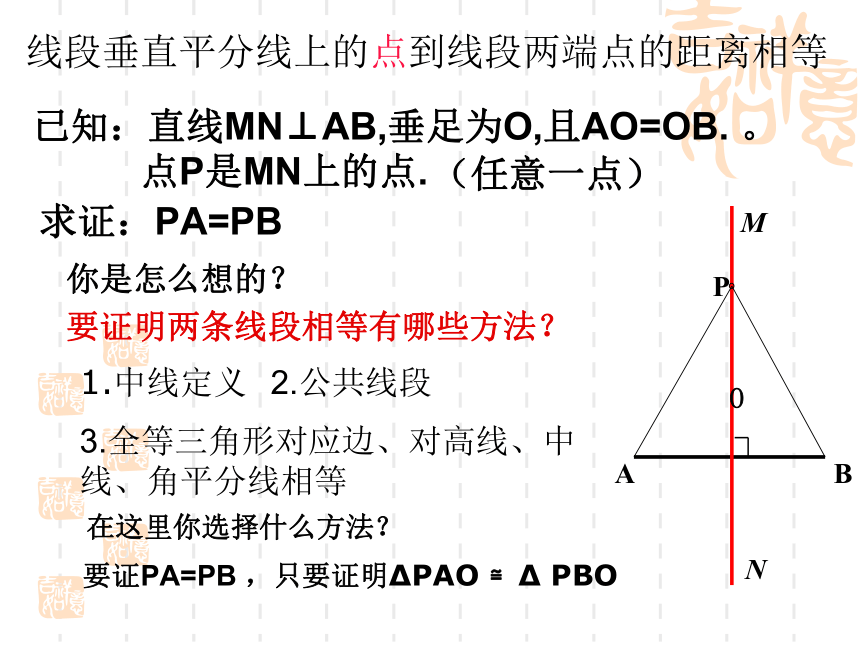
已知:直线MN⊥AB,垂足为O,且AO=OB.
。
你是怎么想的?
O
要证明两条线段相等有哪些方法?
1.中线定义
2.公共线段
3.全等三角形对应边、对高线、中线、角平分线相等
要证PA=PB
,只要证明ΔPAO
≌Δ
PBO
求证:PA=PB
线段垂直平分线上的点到线段两端点的距离相等
在这里你选择什么方法?
点P是MN上的点.
(任意一点)
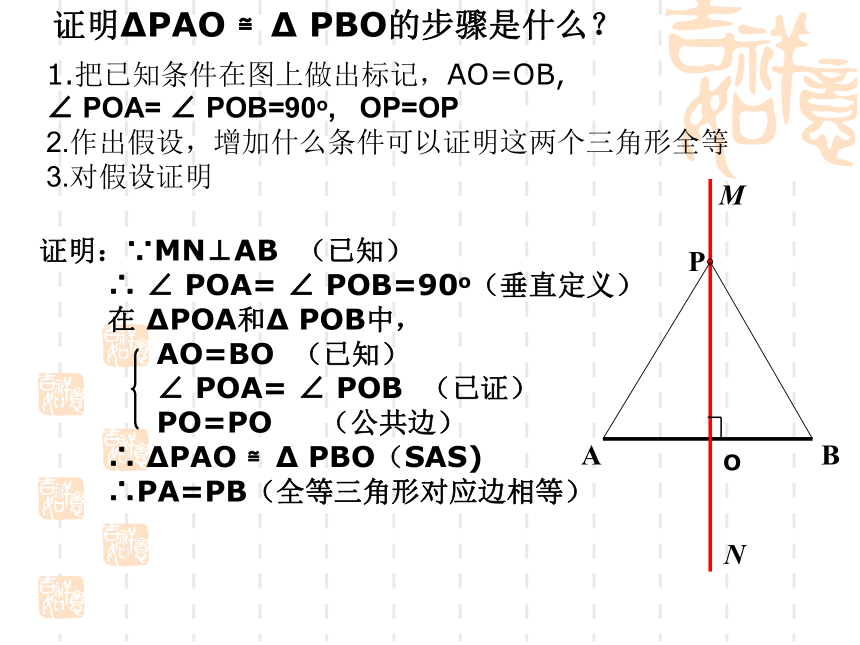
证明:∵MN⊥AB
(已知)
∴
∠
POA=
∠
POB=90o(垂直定义)
在
ΔPOA和Δ
POB中,
AO=BO
(已知)
∠
POA=
∠
POB
(已证)
PO=PO
(公共边)
∴
ΔPAO
≌Δ
PBO(SAS)
∴PA=PB(全等三角形对应边相等)
证明ΔPAO
≌Δ
PBO的步骤是什么?
1.把已知条件在图上做出标记,AO=OB,
∠
POA=
∠
POB=90o,
OP=OP
2.作出假设,增加什么条件可以证明这两个三角形全等
3.对假设证明
A
B
P
M
N
O
任意一点
A
B
P
M
N
线段垂直平分线上的点
到线段两端点的距离相等
一.
线段的垂直平分线的性质:
已知:直线MN⊥AB,垂足为O,AO=OB.结论:
AP=PB,P是MN上任意一点
O
几何语言:
文字语言:
你认为线段的垂直平分线的性质对你以后的学习有什么帮助?
又增加一种证明线段相等的方法
例题1、已知,如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上。
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是___________。
三.线段垂直平分线的运用
例题2.已知:如图,AB=AC=12
cm,AB的垂直平分线分别交AC、AB
于D、E,△ABD的周长等于29
cm,求DC的长.
“△ABD的周长等于29”如何用数学语言表示?
AB+DA+DB=29
二.
线段垂直平分线的运用
DE垂直平分AB?
DA=DB
如图,在ΔABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求ΔBCN的周长。
四.
课堂练习:
1.MN是AB的垂直平分线,你能得到什么?
AN=NB
2.ΔBCN的周长等于什么,
能用数学表达表达吗?
ΔBCN的周长=
BC+BN+NC
四.
课堂练习2:
已知:如图,
△ABC的边BC的垂直平分线DE分别与边AB,
BC交于D、E.
求证:ACD
E
C
A
B
五.课时小结
你有何收获?
从结论出发
1.线段的垂直平分线定义:几何语言
2
.线段的垂直平分线性质
定理:线段垂直平分线上的点到线段两端点的距离相等
①.进一步明确做几何问题的分析方法
3.
线段的垂直平分线应用
分析问题时可以把文字描述用数学表达式表达出来。
②.
回顾证明线段相等的方法
4.
又增加一种证明线段相等的方法
六.作业:
必做
1.课本
第131页
2题,
3
题
2.同步练习
第100页
基础练习15.2
选做
同步练习
第102页
5,
6
第103页
8,
10
一、复习回顾
1.什么叫线段的垂直平分线?(定义)
经过线段的中点并且垂直于这条线段的直线叫这条线段的垂直平分线,又叫中垂线
A
B
O
M
N
几何语言?
已知MN是线段AB
的垂直平分线
则,AO=OB,
MN⊥AB
线段垂直平分线
性质及其应用
15.2
线段的垂直平分线
合肥市南园学校八二班“三杰”的对话:
一天,我班唐俊杰与张良杰同时从家出发到学校,二人约定走路速度一样,结果巧合的是二人同时到达望江路宿松路交口,(望江路宿松路可以看成是垂直的)然后他们沿宿松路一起到了学校,但在教室内发生了如此的对话:
张良杰:如果不考虑我们两家到学校间的建筑物,从学校各修一条路直达我们两人家,我们还是同时同速的话,放学我就比你先到家;
唐俊杰:不对,应该我先到。
为此,二人争论不休,就在这时,李邵杰插了一句:“别吵了,你们同时到。”
张良杰家
唐俊杰家
宿松路望江路交口
宿松路
望江路
南园学校
宿松路与望江路垂直
1.放学谁先到家?
2.如果学校在宿松路上往
前移动,谁先到?
3.你能用一句话总结这个结论吗?
A
B
P
M
N
已知:直线MN⊥AB,垂足为O,且AO=OB.
。
你是怎么想的?
O
要证明两条线段相等有哪些方法?
1.中线定义
2.公共线段
3.全等三角形对应边、对高线、中线、角平分线相等
要证PA=PB
,只要证明ΔPAO
≌Δ
PBO
求证:PA=PB
线段垂直平分线上的点到线段两端点的距离相等
在这里你选择什么方法?
点P是MN上的点.
(任意一点)
证明:∵MN⊥AB
(已知)
∴
∠
POA=
∠
POB=90o(垂直定义)
在
ΔPOA和Δ
POB中,
AO=BO
(已知)
∠
POA=
∠
POB
(已证)
PO=PO
(公共边)
∴
ΔPAO
≌Δ
PBO(SAS)
∴PA=PB(全等三角形对应边相等)
证明ΔPAO
≌Δ
PBO的步骤是什么?
1.把已知条件在图上做出标记,AO=OB,
∠
POA=
∠
POB=90o,
OP=OP
2.作出假设,增加什么条件可以证明这两个三角形全等
3.对假设证明
A
B
P
M
N
O
任意一点
A
B
P
M
N
线段垂直平分线上的点
到线段两端点的距离相等
一.
线段的垂直平分线的性质:
已知:直线MN⊥AB,垂足为O,AO=OB.结论:
AP=PB,P是MN上任意一点
O
几何语言:
文字语言:
你认为线段的垂直平分线的性质对你以后的学习有什么帮助?
又增加一种证明线段相等的方法
例题1、已知,如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上。
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是___________。
三.线段垂直平分线的运用
例题2.已知:如图,AB=AC=12
cm,AB的垂直平分线分别交AC、AB
于D、E,△ABD的周长等于29
cm,求DC的长.
“△ABD的周长等于29”如何用数学语言表示?
AB+DA+DB=29
二.
线段垂直平分线的运用
DE垂直平分AB?
DA=DB
如图,在ΔABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求ΔBCN的周长。
四.
课堂练习:
1.MN是AB的垂直平分线,你能得到什么?
AN=NB
2.ΔBCN的周长等于什么,
能用数学表达表达吗?
ΔBCN的周长=
BC+BN+NC
四.
课堂练习2:
已知:如图,
△ABC的边BC的垂直平分线DE分别与边AB,
BC交于D、E.
求证:AC
E
C
A
B
五.课时小结
你有何收获?
从结论出发
1.线段的垂直平分线定义:几何语言
2
.线段的垂直平分线性质
定理:线段垂直平分线上的点到线段两端点的距离相等
①.进一步明确做几何问题的分析方法
3.
线段的垂直平分线应用
分析问题时可以把文字描述用数学表达式表达出来。
②.
回顾证明线段相等的方法
4.
又增加一种证明线段相等的方法
六.作业:
必做
1.课本
第131页
2题,
3
题
2.同步练习
第100页
基础练习15.2
选做
同步练习
第102页
5,
6
第103页
8,
10
