安徽省六安市皋城中学2020-2021学年第一学期九年级数学期中测试卷(Word版含答案)
文档属性
| 名称 | 安徽省六安市皋城中学2020-2021学年第一学期九年级数学期中测试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 716.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 08:36:38 | ||
图片预览




文档简介
2020—2021年度六安市皋城中学九年级年级期中测试
数学试卷
姓名: 考试时间: 得分:
本试卷共23题,共150分,共7页。考试时间150分钟。考试结束后,将本试卷和答题卡一并交回。
注意事项:
1.答题前,请先将自己的答题卡卷头填写完整。
2.答题时请按要求用笔,作图可先使用铅笔画出。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(本大题共10小题,每小题4分,满分40分)
1、抛物线y=-(x-2)2+1的顶点坐标是 ( )
A.(2,1) B.(-1,2) C.(-1,-1) D.(-1,1)
2、下列图形一定是相似图形的是 ( )
A.两个钝角三角形 B.两个直角三角形 C.两个等腰三角形 D.两个等腰直角三角形
3、二次函数y=ax2的图像如图所示,则不等式ax >a的解集是 ( )
A.x>1 B.x<1 C.x>-1 D.x<-1
4、生活中到处可见黄金分割的美,如图,在设计雕像时,使人使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感,若图中b为2米,则a约为 ( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
5、如图,l1//l2//l3,直线AC、DF与这三条平行线分别交于点A、B、C和点D、?E、F.已知AB=1,?BC=3?,DE=2,?则EF的长为 ( ) A.4 B.5 C.6 D.8
6、已知点(a, m),(b,n)在反比例函数 的图象上,且a>b,则 ( )
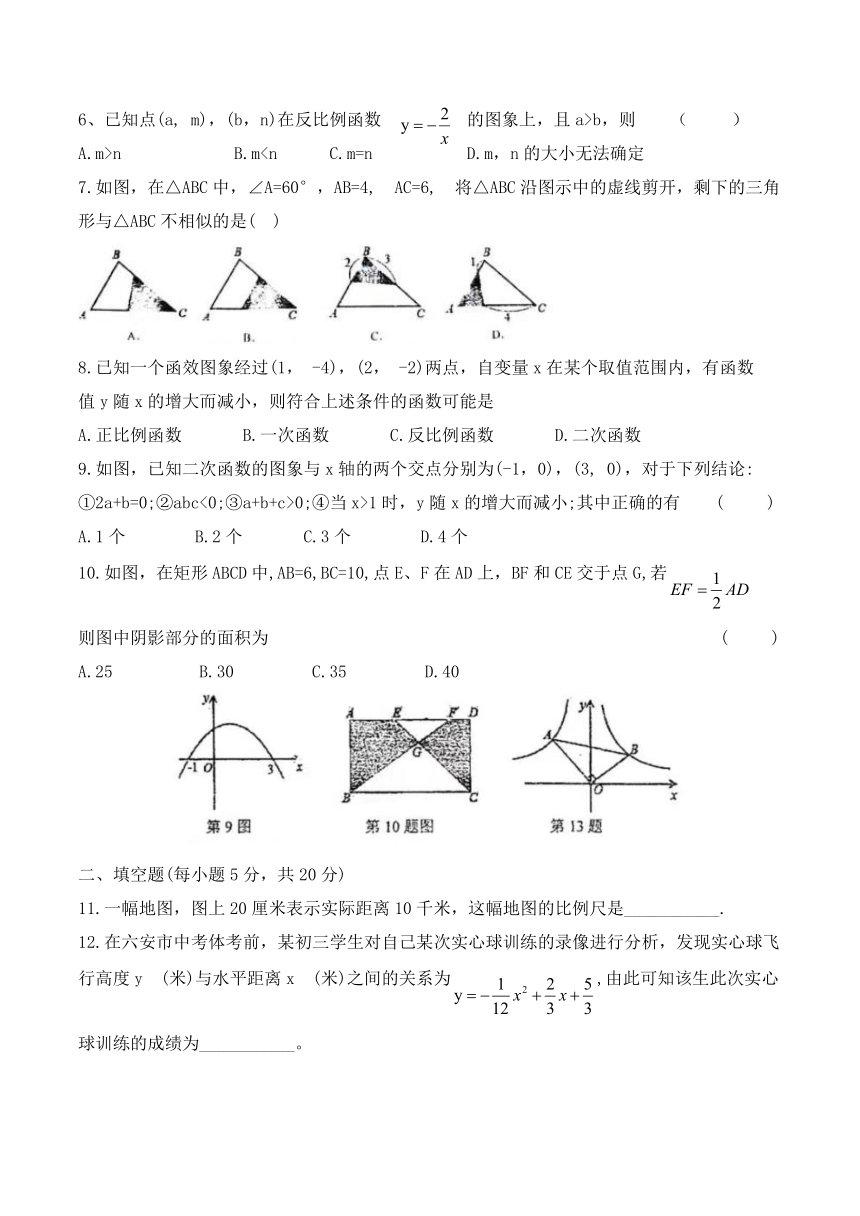
A.m>n B.m7.如图,在△ABC中,∠A=60°,AB=4,?AC=6,?将△ABC沿图示中的虚线剪开,剩下的三角
形与△ABC不相似的是(?)
8.已知一个函效图象经过(1, -4),(2, -2)两点,自变量x在某个取值范围内,有函数
值y随x的增大而减小,则符合上述条件的函数可能是
A.正比例函数 B.一次函数 C.反比例函数 D.二次函数
9.如图,已知二次函数的图象与x轴的两个交点分别为(-1,0),(3, 0),对于下列结论:
①2a+b=0;②abc<0;③a+b+c>0;④当x>1时,y随x的增大而减小;其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,在矩形ABCD中,AB=6,BC=10,点E、F在AD上,BF和CE交于点G,若?
则图中阴影部分的面积为 ( )
A.25 B.30 C.35 D.40
二、填空题(每小题5分,共20分)
11.一幅地图,图上20厘米表示实际距离10千米,这幅地图的比例尺是___________.
12.在六安市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y?(米)与水平距离x?(米)之间的关系为,由此可知该生此次实心球训练的成绩为___________。
13.如图所示,在Rt△AOB中,∠AOB=90° ,OA=4, OB=2,点B在反比例函数y=图象
上,则图中过点A的双曲线解析式是___________.
14.已知二次函数y=ax2+bx+c(a≠0)经过点A?(1,-1),B(3,3),且当1≤x≤3
时,-1≤y≤3,则a的取值范围是__________.
三、简答题(本大题共2小题,每小题8分,满分16分)
15.已知:? (1)求的值: (2)求的值.
16.如图,在边长为1个单位长度的小正方形组成的12×12的网格中,点O、A、B均为其格点.
(1)在给定的网格中,以点O为位似中心将线段AB放大为原来的2倍,得到线段A'B'.
(点A、B的对应点分别为点A'、B'),画出线段A'B'
(2)以线段A'B'为一边,作一个格点四边形A'B'CO,使得格点四边形A'B'CO是轴对称图形。
四、(本大题共2小题,每小题8分,满分16分)
17.?已知二次函数.
(1)求证:该函数图象与x轴一定有两个不同的交点;
(2)若该函数图象关于y轴对称,求图象与x轴的交点坐标.
18.如图正比例函数与反比例函数的图象在第一象限内的交点A的横坐标为4.
(1)求k值;
(2)求它们另一个交点B的坐标:
(3)利用图象直接写出:当x在什么范围内取值时,.
五、(本大题共2小题,每小题10分,满分20分)
19.阅读与计算,请阅读以下材料,井完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则
下面是这个定理的部分证明过程.
证明:如图2,过C作CE//DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分:
(2)填空:如图3,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则
△ABD的周长是________.
20.如图,己知二次函数y=x2+ax+3的图象经过点P(-2,3).
(1)求a的值和图象的项点坐标.
(2)点Q(m,n)在该二次函数图象上.
①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
六、(本大题共2小题,每小题12分,满分24分)
21.如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.
(1)找出图中的相似(不全等)三角形,并证明;
(2)若AE=BE,则长AD与宽AB的比值是多少?
22.如图,在平面直角坐标系中,抛物线与x轴交于A,B(4,0)两点,与
y轴交于点C(0,4).
(I)求此抛物线的函数表达式及点A的坐标;
(2)己知点D(1,-1),在直线AD上方的抛物线上有一-动点P(x,y)(1七、?(本大题14分)
23.如图.在△ABC中,点D,E分别在边AB,BC上,AE与CD相交于点F,过点E作EF//CD
交AC的延长线于点G,若AE平分∠BAC.CE=CF.
(1)①求证:∠ABC=∠ACD:
②求证:△EGC∽△CBD.
(2)如图2,若∠BAC=90°;AD=2,BD=6,求CG的长.
绝密★启用前
2020—2021年度六安市皋城中学九年级年级期中测试
数学试卷
一、选择题
1.A 2.D 3.B 4.A 5.C
6.D 7.C 8.D 9.D 10.C
二、填空题
11.1:50000 12.10 13. 14.
三、解答题
15.解:
(1)∵ ∴= ∴=
(2)由(1)知,=,所以设y=2k,x=2k。
则
16.解:
解:(1) ,b=k+1, c=k
则△=b2 -4ac=(k+1)2-4×k
=k2+2k+1-k=k2+k+1
=k2+k+
=(k+)2+>0
故该函数图像与x轴有两个不同的交点。
∵该函数图像关于y轴对称,则对称轴x==0,
则k+1=0,k=-1
则y=,与x轴交点坐标y=0,即=0
则x=±2
∴交点坐标为(2,0)(-2,0)
解:(1)将A的横坐标4代入,得y1=2 ∴A(4,2)∴k=8
、联立解析式成方程组,得;;∴B(-4,-2)
x>4或-4<x<0
19.解:(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴,即,
∴BD=,
∴AD==
∴△ABD的周长=.
20.解:(1)把点P?(-2,?3)?代入y=x2+ax+3中,
∴a=2,
∴y=x2+2x+3,
.顶点坐标为(-1,?2)?;
(2)①当m=2时,n=11,
②点Q到y轴的距离小于2,
∴?<2,
∴-2∴2≤n<11;
21、解:(1)AE=BE?,设AE=2k,则BE=3k,AB=5k.
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,CD=AB=5k,AD=BC.
将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处,
∴∠EFC=∠B=90°,EF=?EB=?3k,CF=?BC,
∴∠AFE+∠DFC=?90°,∠DFC+∠FCD=?90°
∴∠DCF=∠AFE,
∴?cos∠AFE=?cos∠DCF.
在Rt△AEF中,∵∠A=90°,?AE=2k,EF=?3k?,
∴AF=
∴
∴CF=
∴AD=BC=CF=
∴长AD与宽AB的比值是=
22、(1)、A(0,2) (2)
23、CG=4
数学试卷
姓名: 考试时间: 得分:
本试卷共23题,共150分,共7页。考试时间150分钟。考试结束后,将本试卷和答题卡一并交回。
注意事项:
1.答题前,请先将自己的答题卡卷头填写完整。
2.答题时请按要求用笔,作图可先使用铅笔画出。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(本大题共10小题,每小题4分,满分40分)
1、抛物线y=-(x-2)2+1的顶点坐标是 ( )
A.(2,1) B.(-1,2) C.(-1,-1) D.(-1,1)
2、下列图形一定是相似图形的是 ( )
A.两个钝角三角形 B.两个直角三角形 C.两个等腰三角形 D.两个等腰直角三角形
3、二次函数y=ax2的图像如图所示,则不等式ax >a的解集是 ( )
A.x>1 B.x<1 C.x>-1 D.x<-1
4、生活中到处可见黄金分割的美,如图,在设计雕像时,使人使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感,若图中b为2米,则a约为 ( )
A.1.24米 B.1.38米 C.1.42米 D.1.62米
5、如图,l1//l2//l3,直线AC、DF与这三条平行线分别交于点A、B、C和点D、?E、F.已知AB=1,?BC=3?,DE=2,?则EF的长为 ( ) A.4 B.5 C.6 D.8
6、已知点(a, m),(b,n)在反比例函数 的图象上,且a>b,则 ( )
A.m>n B.m
形与△ABC不相似的是(?)
8.已知一个函效图象经过(1, -4),(2, -2)两点,自变量x在某个取值范围内,有函数
值y随x的增大而减小,则符合上述条件的函数可能是
A.正比例函数 B.一次函数 C.反比例函数 D.二次函数
9.如图,已知二次函数的图象与x轴的两个交点分别为(-1,0),(3, 0),对于下列结论:
①2a+b=0;②abc<0;③a+b+c>0;④当x>1时,y随x的增大而减小;其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,在矩形ABCD中,AB=6,BC=10,点E、F在AD上,BF和CE交于点G,若?
则图中阴影部分的面积为 ( )
A.25 B.30 C.35 D.40
二、填空题(每小题5分,共20分)
11.一幅地图,图上20厘米表示实际距离10千米,这幅地图的比例尺是___________.
12.在六安市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y?(米)与水平距离x?(米)之间的关系为,由此可知该生此次实心球训练的成绩为___________。
13.如图所示,在Rt△AOB中,∠AOB=90° ,OA=4, OB=2,点B在反比例函数y=图象
上,则图中过点A的双曲线解析式是___________.
14.已知二次函数y=ax2+bx+c(a≠0)经过点A?(1,-1),B(3,3),且当1≤x≤3
时,-1≤y≤3,则a的取值范围是__________.
三、简答题(本大题共2小题,每小题8分,满分16分)
15.已知:? (1)求的值: (2)求的值.
16.如图,在边长为1个单位长度的小正方形组成的12×12的网格中,点O、A、B均为其格点.
(1)在给定的网格中,以点O为位似中心将线段AB放大为原来的2倍,得到线段A'B'.
(点A、B的对应点分别为点A'、B'),画出线段A'B'
(2)以线段A'B'为一边,作一个格点四边形A'B'CO,使得格点四边形A'B'CO是轴对称图形。
四、(本大题共2小题,每小题8分,满分16分)
17.?已知二次函数.
(1)求证:该函数图象与x轴一定有两个不同的交点;
(2)若该函数图象关于y轴对称,求图象与x轴的交点坐标.
18.如图正比例函数与反比例函数的图象在第一象限内的交点A的横坐标为4.
(1)求k值;
(2)求它们另一个交点B的坐标:
(3)利用图象直接写出:当x在什么范围内取值时,.
五、(本大题共2小题,每小题10分,满分20分)
19.阅读与计算,请阅读以下材料,井完成相应的问题.
角平分线分线段成比例定理:如图1,在△ABC中,AD平分∠BAC,则
下面是这个定理的部分证明过程.
证明:如图2,过C作CE//DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分:
(2)填空:如图3,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则
△ABD的周长是________.
20.如图,己知二次函数y=x2+ax+3的图象经过点P(-2,3).
(1)求a的值和图象的项点坐标.
(2)点Q(m,n)在该二次函数图象上.
①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
六、(本大题共2小题,每小题12分,满分24分)
21.如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.
(1)找出图中的相似(不全等)三角形,并证明;
(2)若AE=BE,则长AD与宽AB的比值是多少?
22.如图,在平面直角坐标系中,抛物线与x轴交于A,B(4,0)两点,与
y轴交于点C(0,4).
(I)求此抛物线的函数表达式及点A的坐标;
(2)己知点D(1,-1),在直线AD上方的抛物线上有一-动点P(x,y)(1
23.如图.在△ABC中,点D,E分别在边AB,BC上,AE与CD相交于点F,过点E作EF//CD
交AC的延长线于点G,若AE平分∠BAC.CE=CF.
(1)①求证:∠ABC=∠ACD:
②求证:△EGC∽△CBD.
(2)如图2,若∠BAC=90°;AD=2,BD=6,求CG的长.
绝密★启用前
2020—2021年度六安市皋城中学九年级年级期中测试
数学试卷
一、选择题
1.A 2.D 3.B 4.A 5.C
6.D 7.C 8.D 9.D 10.C
二、填空题
11.1:50000 12.10 13. 14.
三、解答题
15.解:
(1)∵ ∴= ∴=
(2)由(1)知,=,所以设y=2k,x=2k。
则
16.解:
解:(1) ,b=k+1, c=k
则△=b2 -4ac=(k+1)2-4×k
=k2+2k+1-k=k2+k+1
=k2+k+
=(k+)2+>0
故该函数图像与x轴有两个不同的交点。
∵该函数图像关于y轴对称,则对称轴x==0,
则k+1=0,k=-1
则y=,与x轴交点坐标y=0,即=0
则x=±2
∴交点坐标为(2,0)(-2,0)
解:(1)将A的横坐标4代入,得y1=2 ∴A(4,2)∴k=8
、联立解析式成方程组,得;;∴B(-4,-2)
x>4或-4<x<0
19.解:(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴,即,
∴BD=,
∴AD==
∴△ABD的周长=.
20.解:(1)把点P?(-2,?3)?代入y=x2+ax+3中,
∴a=2,
∴y=x2+2x+3,
.顶点坐标为(-1,?2)?;
(2)①当m=2时,n=11,
②点Q到y轴的距离小于2,
∴?<2,
∴-2
21、解:(1)AE=BE?,设AE=2k,则BE=3k,AB=5k.
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,CD=AB=5k,AD=BC.
将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处,
∴∠EFC=∠B=90°,EF=?EB=?3k,CF=?BC,
∴∠AFE+∠DFC=?90°,∠DFC+∠FCD=?90°
∴∠DCF=∠AFE,
∴?cos∠AFE=?cos∠DCF.
在Rt△AEF中,∵∠A=90°,?AE=2k,EF=?3k?,
∴AF=
∴
∴CF=
∴AD=BC=CF=
∴长AD与宽AB的比值是=
22、(1)、A(0,2) (2)
23、CG=4
同课章节目录
