沪科版数学七年级上册2.2 去括号 教案
文档属性
| 名称 | 沪科版数学七年级上册2.2 去括号 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 22.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 16:12:43 | ||
图片预览

文档简介
课题《去括号》
教学设计
教材分析
本节课教材从具体问题出发,尝试从不同角度寻求解决问题的办法.通过观察、思考、讨论,从中探究出去括号法则,再通过例题教学和练习,熟练法则的应用,为整式的运算作准备.
学情分析
学生已经初步掌握了代数式、整式、合并同类型的基本知识,为这节课的去括号做好了知识准备。但学生的基础还不尽相同,部分同学对本节课的学习还将会存在困难。
设计理念
本节课采用的教学模式:自学教材—自主探究—合作探究—达标检测
教学目标
知识与技能:
1.经历去括号法则的形成过程,理解去括号的意义。
2.掌握去括号法则,能用去括号法则进行运算,培养运算能力。
3.能利用去括号法则解决简单的问题。
过程与方法:
1.通过观察、思考、讨论等活动自己概括出去括号的法则,加深对“+”“-”符号的认识,体会从特殊到一般和从一般到特殊的数学思想方法.
2.应用去括号法则时不要只考虑括号内的部分项,而要考虑括号内的每一项.
教学重点
重点:去括号法则及其应用.
教学难点
难点:括号前是“-”号的去括号法则.
教学准备
导学卡
教学过程
三个阶段
学习内容
教师行为
期望学生行为
我的做法
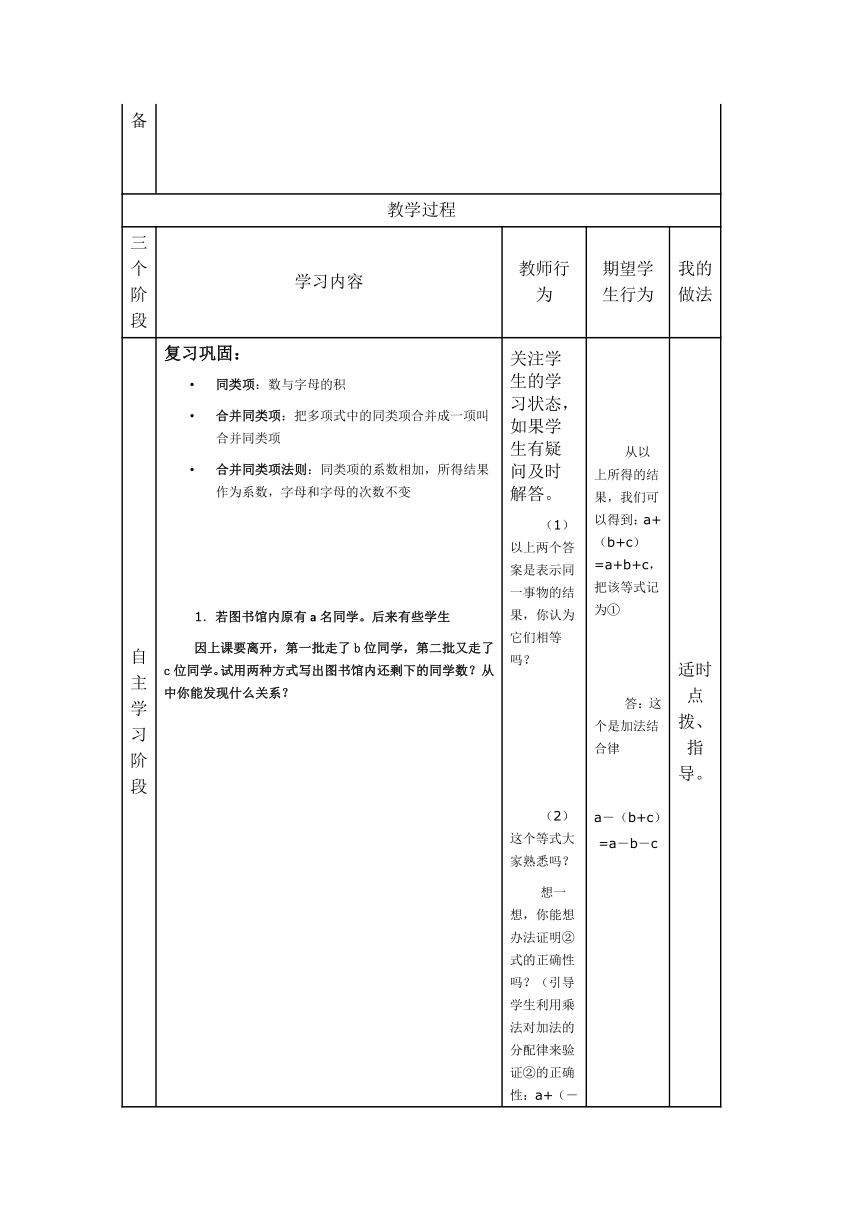
自主学习阶段
复习巩固:
同类项:数与字母的积
合并同类项:把多项式中的同类项合并成一项叫合并同类项
合并同类项法则:同类项的系数相加,所得结果作为系数,字母和字母的次数不变
?
?
?
1.若图书馆内原有a名同学。后来有些学生
因上课要离开,第一批走了b位同学,第二批又走了c位同学。试用两种方式写出图书馆内还剩下的同学数?从中你能发现什么关系?
关注学生的学习状态,如果学生有疑问及时解答。
(1)以上两个答案是表示同一事物的结果,你认为它们相等吗?
?
?
?
?
(2)这个等式大家熟悉吗?
想一想,你能想办法证明②式的正确性吗?(引导学生利用乘法对加法的分配律来验证②的正确性:a+(-1)(b+c)
?
?
?
从以上所得的结果,我们可以得到:a+(b+c)=a+b+c,把该等式记为①
?
?
答:这个是加法结合律
?
a-(b+c)=a-b-c
适时点拨、指导。
合作交流阶段
化简下列式子:
1.-(3m-2n+1)
2.3m+(2n-p)
(从学生熟悉的知识引出新知识,不但是可行的,而且是科学的,符合学生的认知规律.在复习旧知识时,不是简单的重复,而应注意本课的教学目标,找准新知识的切入点.)
(三)归纳总结
去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,原来括号里的各项都不变符号.
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号.
师提示法则的特征,指出:去括号时,要连同括号前的符号一同去掉.
例2?先去括号,再合并同类项:
①(?5a+3b)+(3a-2b);
②2(4x-6y)-3(2x+3y-1).
?
?
在肯定了上面两式的基础上,请同学们用以前学过的知识,化简下列式子:
?
?
我们将首先从以上四个等式入手,看看等号左边的多项式为什么会等于等号右边的多项式,这其中有没有什么规律?如果有,又是怎样的规律呢?
?
?
强调:要特别注意括号前有数字因数的情形.先用分配律数字与括号内的各项相乘,然后再去括号,熟练后,也可省略第二步,直接去括号
?
?
?
?
小组讨论,小组代表发言,小组之间相互补充,使之趋于完整.
?
讲解点拨
?
并作必要强调:在板书上用彩粉笔作出“重点”标号,以引起学生注意,强调“各项”,“不变”,“改变”的含义.
巩固达标阶段
1.口答:去括号
(1)a
+
(–
b
+
c
)
=
(
2
)
(
a
–
b
)
–
(
c
+
d
)
=
(
3
)
–
(–
a
+
b
)
–
c
=
(
4
)
–
(2x
–
y
)
–
(
–
x2
+
y2
)
=
2.判断下列计算是否正确,错的请说明理由:
学生完成后对于规律性的问题教师进行总结
能够准确完成巩固达标题,发现解决此类问题的一般规律。
对难点进行讲解,引导学生完成相应的习题。
板书设计
4.3去括号
去括号法则:
1.括号前面是“+”号,把括号和它前面的“+”号去掉,括号里的各项都不变符号.
2.括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号.
???????????????????????????????
课后反思
?
教学设计
教材分析
本节课教材从具体问题出发,尝试从不同角度寻求解决问题的办法.通过观察、思考、讨论,从中探究出去括号法则,再通过例题教学和练习,熟练法则的应用,为整式的运算作准备.
学情分析
学生已经初步掌握了代数式、整式、合并同类型的基本知识,为这节课的去括号做好了知识准备。但学生的基础还不尽相同,部分同学对本节课的学习还将会存在困难。
设计理念
本节课采用的教学模式:自学教材—自主探究—合作探究—达标检测
教学目标
知识与技能:
1.经历去括号法则的形成过程,理解去括号的意义。
2.掌握去括号法则,能用去括号法则进行运算,培养运算能力。
3.能利用去括号法则解决简单的问题。
过程与方法:
1.通过观察、思考、讨论等活动自己概括出去括号的法则,加深对“+”“-”符号的认识,体会从特殊到一般和从一般到特殊的数学思想方法.
2.应用去括号法则时不要只考虑括号内的部分项,而要考虑括号内的每一项.
教学重点
重点:去括号法则及其应用.
教学难点
难点:括号前是“-”号的去括号法则.
教学准备
导学卡
教学过程
三个阶段
学习内容
教师行为
期望学生行为
我的做法
自主学习阶段
复习巩固:
同类项:数与字母的积
合并同类项:把多项式中的同类项合并成一项叫合并同类项
合并同类项法则:同类项的系数相加,所得结果作为系数,字母和字母的次数不变
?
?
?
1.若图书馆内原有a名同学。后来有些学生
因上课要离开,第一批走了b位同学,第二批又走了c位同学。试用两种方式写出图书馆内还剩下的同学数?从中你能发现什么关系?
关注学生的学习状态,如果学生有疑问及时解答。
(1)以上两个答案是表示同一事物的结果,你认为它们相等吗?
?
?
?
?
(2)这个等式大家熟悉吗?
想一想,你能想办法证明②式的正确性吗?(引导学生利用乘法对加法的分配律来验证②的正确性:a+(-1)(b+c)
?
?
?
从以上所得的结果,我们可以得到:a+(b+c)=a+b+c,把该等式记为①
?
?
答:这个是加法结合律
?
a-(b+c)=a-b-c
适时点拨、指导。
合作交流阶段
化简下列式子:
1.-(3m-2n+1)
2.3m+(2n-p)
(从学生熟悉的知识引出新知识,不但是可行的,而且是科学的,符合学生的认知规律.在复习旧知识时,不是简单的重复,而应注意本课的教学目标,找准新知识的切入点.)
(三)归纳总结
去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,原来括号里的各项都不变符号.
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号.
师提示法则的特征,指出:去括号时,要连同括号前的符号一同去掉.
例2?先去括号,再合并同类项:
①(?5a+3b)+(3a-2b);
②2(4x-6y)-3(2x+3y-1).
?
?
在肯定了上面两式的基础上,请同学们用以前学过的知识,化简下列式子:
?
?
我们将首先从以上四个等式入手,看看等号左边的多项式为什么会等于等号右边的多项式,这其中有没有什么规律?如果有,又是怎样的规律呢?
?
?
强调:要特别注意括号前有数字因数的情形.先用分配律数字与括号内的各项相乘,然后再去括号,熟练后,也可省略第二步,直接去括号
?
?
?
?
小组讨论,小组代表发言,小组之间相互补充,使之趋于完整.
?
讲解点拨
?
并作必要强调:在板书上用彩粉笔作出“重点”标号,以引起学生注意,强调“各项”,“不变”,“改变”的含义.
巩固达标阶段
1.口答:去括号
(1)a
+
(–
b
+
c
)
=
(
2
)
(
a
–
b
)
–
(
c
+
d
)
=
(
3
)
–
(–
a
+
b
)
–
c
=
(
4
)
–
(2x
–
y
)
–
(
–
x2
+
y2
)
=
2.判断下列计算是否正确,错的请说明理由:
学生完成后对于规律性的问题教师进行总结
能够准确完成巩固达标题,发现解决此类问题的一般规律。
对难点进行讲解,引导学生完成相应的习题。
板书设计
4.3去括号
去括号法则:
1.括号前面是“+”号,把括号和它前面的“+”号去掉,括号里的各项都不变符号.
2.括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号.
???????????????????????????????
课后反思
?
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
