华东师大版数学九年级上册-25.2 列举所有机会均等的结果 课件(32张)
文档属性
| 名称 | 华东师大版数学九年级上册-25.2 列举所有机会均等的结果 课件(32张) |  | |
| 格式 | zip | ||
| 文件大小 | 340.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 18:19:15 | ||
图片预览









文档简介
(共32张PPT)
25.2.3列举所有机会均等的结果
驶向胜利的彼岸
1.理解可以理性地用列表法或树状图法来列举所有机会均等的结果;
2.掌握用列表或树状图法求事件的概率.
2.概率的计算公式是什么?
表示一个事件发生的可能性的大小的这个数,叫做该事件的概率。
3.计算概率最关键的有两点:
1.什么是概率?
关注的结果的个数
P(事件发生)=
所有机会均等的结果的个数
(1)要清楚我们关注的是发生哪个或哪些结果;
(2)要清楚所有机会均等的结果。
一、创设情境
小明、小颖、小凡都想去看周末电影,但只有一张电影票,三人决定一起做游戏,谁获胜谁就去看电影。游戏规则如下:连续掷两枚质地均匀的硬币,若两枚正面朝上,则小明获胜;
若两枚反面朝上,则小颖获胜;若一枚正面朝上,一枚反面朝上,则小凡获胜。你认为这个游戏公平吗?
探究1.小明、小颖、小凡做“石头,剪刀,布”的游戏,游戏规则如下:小明、小颖玩“石头,剪刀,布”的游戏,如果两人的手势相同,那么小凡获胜;如果两人的手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者。
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏公平吗?
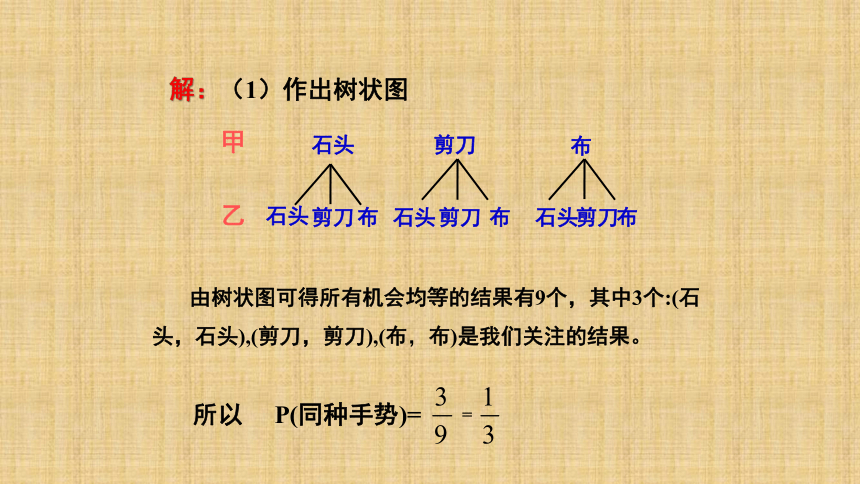
解:(1)作出树状图
甲
石头
剪刀
布
乙
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
由树状图可得所有机会均等的结果有9个,其中3个:(石头,石头),(剪刀,剪刀),(布,布)是我们关注的结果。
所以
P(同种手势)=
=
由表格可得所有机会均等的结果有9个,其中不分胜负的结果有3个。
(剪刀,布)
(石头,布)
布
(剪刀,布)
(剪刀,石头)
剪刀
(石头,布)
(石头,剪刀)
石头
布
剪刀
石头
小颖出的拳
小明出的拳
(2)列表如下:
所以
P(小凡获胜)=
(石头,石头)
(
剪刀,剪刀)
(布,布)
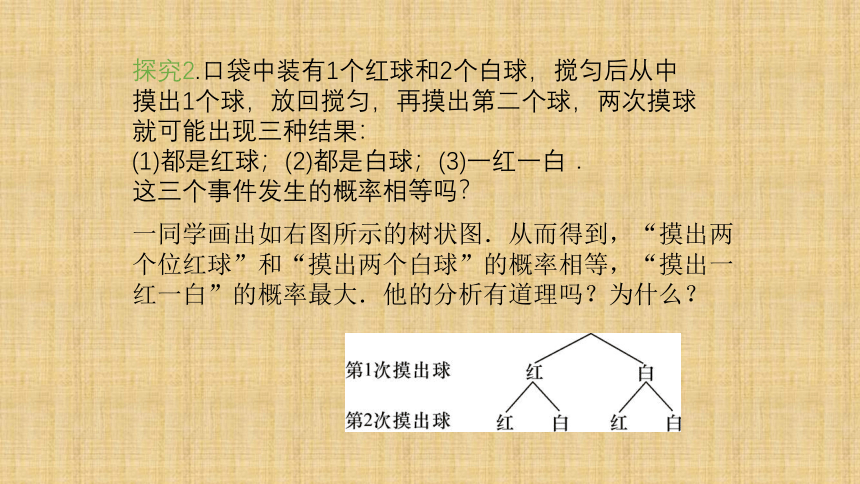
探究2.口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第二个球,两次摸球就可能出现三种结果:
(1)都是红球;(2)都是白球;(3)一红一白.
这三个事件发生的概率相等吗?
一同学画出如右图所示的树状图.从而得到,“摸出两个位红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大.他的分析有道理吗?为什么?
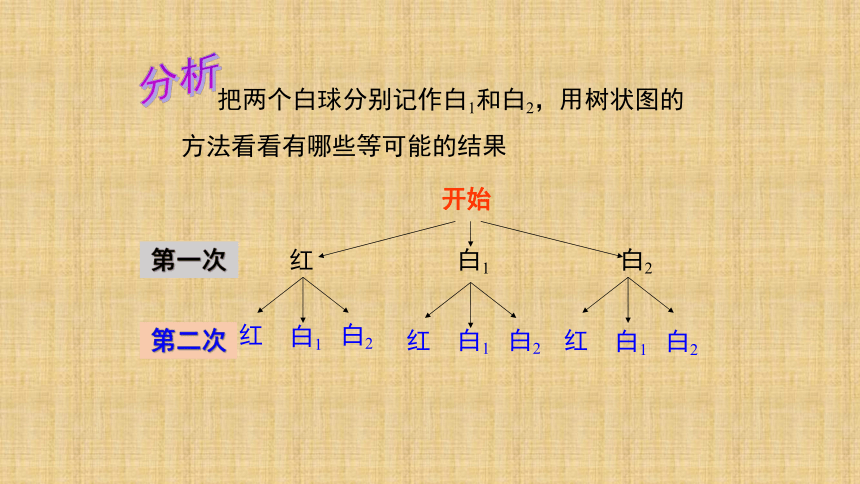
把两个白球分别记作白1和白2,用树状图的方法看看有哪些等可能的结果
分析
开始
红
白1
白2
红
白1
白2
红
白1
白2
红
白1
白2
第一次
第二次
从图中可以看出,一共有9种可能的结果,这9个事件出现的概率相等,在摸出“两红”,“两白”,“一红一白”这三个事件中,“摸出
”概率最小,等于
,“摸出一红一白”和“摸出_____”的概率相等,都是______.
两红
两白
变式训练:口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中“一红一白”的概率.
投掷两枚普通的正方面体骰子,所得点数之积有多少种可能?点数之积为多少的概率最大,其概率是多少?
分析:这一问题用树状图分析是否简单?
如果利用表格来列举所有可能得到的点数之积是否可行?试试看?
探究2
一
二
1
2
3
4
5
6
1
1
2
3
4
5
6
2
2
4
6
8
10
12
3
3
6
9
12
15
18
4
4
8
12
16
20
24
5
5
10
15
20
25
30
6
6
12
18
24
30
36
解:列表如下:
由表中每个格子里乘积出现的概率相等,从中可以看出积为
的概率最大,其概率等于
.
总结:
在表格中按规律分别组合,列出所有可能的结果,再从中选出符合事件结果的个数,是分析概率的另一方法。在机会均等的结果较多时,适合用列表法求概率.
三、练习反馈:
1.某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验A考查的概率是______;
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;
(3)他们三人都参加实验A考查的概率是______.
2.如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.
用树状图法列举时应注意同时取出还是放回后再抽取,两种方法不一样.
五.布置作业:
P155习题25.2第7题
P160复习题第10题,第11题(选做)
1.有的同学认为:抛掷三枚普通硬币,硬币落地后只可能出现4种情况:(1)全是正面,(2)两正一反;(3)两反一正;(4)全是反面.因此这四个事件出现的概率相等,你同意这种说法吗?为什么?
解:画树状图分析如下:
开始
硬币1
正
反
硬币2
硬币3
正
反
正
反
正
反
正
反
正
反
正
反
开始
正
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
反
第一枚
第二枚
随机掷两枚均匀的硬币两次,
两次正面朝上的概率是多少?
总共有4种结果,每种结果出现的可能性相同,而两个正面朝上的结果有1种:
P=1/4.
以上的解题过程我们常把它称为画树状图求概率。它可以帮助我们分析问题,而且可以避免重复和遗漏,既直观又条理分明.
随机掷两枚均匀的硬币两次,
两次正面朝上的概率是多少?
例4
抛掷一枚普通的硬币3次.有人说连续掷出三个正面和先掷出两个正面再掷出一个反面的机会是一样的.你同意吗?
分析
对于第1次抛掷,可能出现的结果是正面或反面;对于第2、3次抛掷来说也是这样。而且每次硬币出现正面或反面的概率都相等。由此,我们可以画出树状图.
开始
第一次
正
反
第二次
正
反
正
反
第三次
正
反
正
正
正
反
反
反
从上至下每一条路径就是一种可能的结果,而且每种结果发生的概率相等.
正正正
正正反
正反正
反正正
正反反
反正反
反反正
反反反
解:
综上,共有以下八种机会均等的结果:
P(正正正)=P(正正反)=
所以,这一说法正确.
画树状图求概率的步骤:
①把第一个因素所有可能的结果列举出来.
②随着事件的发展,在第一个因素的每一种可能上列出第二个因素的所有的可能.
③在第二步列出的每一个可能上列出第三个因素的所有的可能.
……
归纳
“石头,剪刀,布”是一个广为流传的游戏,游戏时甲乙双方每次做“石头”,“剪刀”,“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负。
假定甲乙两人每次都是等可能地做这三种手势,那么一次比赛时两人做同种手势(即不分胜负)的概率是多少?
探究3
口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第2个球,两次摸球就可能出现3种结果:
(1)都是红球;
(2)都是白球;
(3)一红一白.
这三个事件发生的概率相等吗?
探究1
在分析上面问题时,一位同学画出如下图所示的树状图.
开始
第一次
红
白
红
白
红
白
第二次
从而得到,“摸出两个红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大.
他的分析有道理吗?为什么?
把两个白球分别记作白1和白2,用树状图的方法看看有哪些等可能的结果
分析
开始
红
白1
白2
红
白1
白2
红
白1
白2
红
白1
白2
第一次
第二次
口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第2个球,两次摸球就可能出现3种结果:
(1)都是红球;
(2)都是白球;
(3)一红一白.
这三个事件发生的概率相等吗?
探究1
先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
由以上数状图可以看出来:
所以以上说法不正确.
2.有两双手套,形状、大小,完全相同,只有颜色不同。黑暗中,任意抽出两只配成一双的概率是多少?
解:
假设两双手套的颜色分别为红、黑,如下分析:
红1
黑1
黑2
红2
红1
黑1
黑2
红2
红1
黑1
黑2
红2
红1
黑1
黑2
红2
开始
第一次
第二次
P(配成一双)
=
=
由以上数状图可以看出来:
共有以下12种机会均等的结果:
3.下面是两个可以自由转动的转盘,每个转盘被分成了三个相等的扇形,小明和小亮用它们做配紫色(红色与蓝色能配成紫色)游戏,你认为配成紫色与配不成紫色的概率相同吗?
解:所有可能出现的结果如下:
A
红
红
蓝
(红,红)
(蓝,红)
(蓝,红)
(红,红)
(蓝,红)
(蓝,红)
(红,蓝)
(蓝,蓝)
(蓝,蓝)
B
红
蓝
蓝
一共有9种结果,每种结果出现的可能性相同,(红,蓝)能配紫色的有5种,概率为5/9;不能配紫色的有4种,概率为4/9,它们的概率不相同。
25.2.3列举所有机会均等的结果
驶向胜利的彼岸
1.理解可以理性地用列表法或树状图法来列举所有机会均等的结果;
2.掌握用列表或树状图法求事件的概率.
2.概率的计算公式是什么?
表示一个事件发生的可能性的大小的这个数,叫做该事件的概率。
3.计算概率最关键的有两点:
1.什么是概率?
关注的结果的个数
P(事件发生)=
所有机会均等的结果的个数
(1)要清楚我们关注的是发生哪个或哪些结果;
(2)要清楚所有机会均等的结果。
一、创设情境
小明、小颖、小凡都想去看周末电影,但只有一张电影票,三人决定一起做游戏,谁获胜谁就去看电影。游戏规则如下:连续掷两枚质地均匀的硬币,若两枚正面朝上,则小明获胜;
若两枚反面朝上,则小颖获胜;若一枚正面朝上,一枚反面朝上,则小凡获胜。你认为这个游戏公平吗?
探究1.小明、小颖、小凡做“石头,剪刀,布”的游戏,游戏规则如下:小明、小颖玩“石头,剪刀,布”的游戏,如果两人的手势相同,那么小凡获胜;如果两人的手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者。
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏公平吗?
解:(1)作出树状图
甲
石头
剪刀
布
乙
石头
剪刀
布
石头
剪刀
布
石头
剪刀
布
由树状图可得所有机会均等的结果有9个,其中3个:(石头,石头),(剪刀,剪刀),(布,布)是我们关注的结果。
所以
P(同种手势)=
=
由表格可得所有机会均等的结果有9个,其中不分胜负的结果有3个。
(剪刀,布)
(石头,布)
布
(剪刀,布)
(剪刀,石头)
剪刀
(石头,布)
(石头,剪刀)
石头
布
剪刀
石头
小颖出的拳
小明出的拳
(2)列表如下:
所以
P(小凡获胜)=
(石头,石头)
(
剪刀,剪刀)
(布,布)
探究2.口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第二个球,两次摸球就可能出现三种结果:
(1)都是红球;(2)都是白球;(3)一红一白.
这三个事件发生的概率相等吗?
一同学画出如右图所示的树状图.从而得到,“摸出两个位红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大.他的分析有道理吗?为什么?
把两个白球分别记作白1和白2,用树状图的方法看看有哪些等可能的结果
分析
开始
红
白1
白2
红
白1
白2
红
白1
白2
红
白1
白2
第一次
第二次
从图中可以看出,一共有9种可能的结果,这9个事件出现的概率相等,在摸出“两红”,“两白”,“一红一白”这三个事件中,“摸出
”概率最小,等于
,“摸出一红一白”和“摸出_____”的概率相等,都是______.
两红
两白
变式训练:口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中“一红一白”的概率.
投掷两枚普通的正方面体骰子,所得点数之积有多少种可能?点数之积为多少的概率最大,其概率是多少?
分析:这一问题用树状图分析是否简单?
如果利用表格来列举所有可能得到的点数之积是否可行?试试看?
探究2
一
二
1
2
3
4
5
6
1
1
2
3
4
5
6
2
2
4
6
8
10
12
3
3
6
9
12
15
18
4
4
8
12
16
20
24
5
5
10
15
20
25
30
6
6
12
18
24
30
36
解:列表如下:
由表中每个格子里乘积出现的概率相等,从中可以看出积为
的概率最大,其概率等于
.
总结:
在表格中按规律分别组合,列出所有可能的结果,再从中选出符合事件结果的个数,是分析概率的另一方法。在机会均等的结果较多时,适合用列表法求概率.
三、练习反馈:
1.某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验A考查的概率是______;
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;
(3)他们三人都参加实验A考查的概率是______.
2.如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.
用树状图法列举时应注意同时取出还是放回后再抽取,两种方法不一样.
五.布置作业:
P155习题25.2第7题
P160复习题第10题,第11题(选做)
1.有的同学认为:抛掷三枚普通硬币,硬币落地后只可能出现4种情况:(1)全是正面,(2)两正一反;(3)两反一正;(4)全是反面.因此这四个事件出现的概率相等,你同意这种说法吗?为什么?
解:画树状图分析如下:
开始
硬币1
正
反
硬币2
硬币3
正
反
正
反
正
反
正
反
正
反
正
反
开始
正
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
反
第一枚
第二枚
随机掷两枚均匀的硬币两次,
两次正面朝上的概率是多少?
总共有4种结果,每种结果出现的可能性相同,而两个正面朝上的结果有1种:
P=1/4.
以上的解题过程我们常把它称为画树状图求概率。它可以帮助我们分析问题,而且可以避免重复和遗漏,既直观又条理分明.
随机掷两枚均匀的硬币两次,
两次正面朝上的概率是多少?
例4
抛掷一枚普通的硬币3次.有人说连续掷出三个正面和先掷出两个正面再掷出一个反面的机会是一样的.你同意吗?
分析
对于第1次抛掷,可能出现的结果是正面或反面;对于第2、3次抛掷来说也是这样。而且每次硬币出现正面或反面的概率都相等。由此,我们可以画出树状图.
开始
第一次
正
反
第二次
正
反
正
反
第三次
正
反
正
正
正
反
反
反
从上至下每一条路径就是一种可能的结果,而且每种结果发生的概率相等.
正正正
正正反
正反正
反正正
正反反
反正反
反反正
反反反
解:
综上,共有以下八种机会均等的结果:
P(正正正)=P(正正反)=
所以,这一说法正确.
画树状图求概率的步骤:
①把第一个因素所有可能的结果列举出来.
②随着事件的发展,在第一个因素的每一种可能上列出第二个因素的所有的可能.
③在第二步列出的每一个可能上列出第三个因素的所有的可能.
……
归纳
“石头,剪刀,布”是一个广为流传的游戏,游戏时甲乙双方每次做“石头”,“剪刀”,“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负。
假定甲乙两人每次都是等可能地做这三种手势,那么一次比赛时两人做同种手势(即不分胜负)的概率是多少?
探究3
口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第2个球,两次摸球就可能出现3种结果:
(1)都是红球;
(2)都是白球;
(3)一红一白.
这三个事件发生的概率相等吗?
探究1
在分析上面问题时,一位同学画出如下图所示的树状图.
开始
第一次
红
白
红
白
红
白
第二次
从而得到,“摸出两个红球”和“摸出两个白球”的概率相等,“摸出一红一白”的概率最大.
他的分析有道理吗?为什么?
把两个白球分别记作白1和白2,用树状图的方法看看有哪些等可能的结果
分析
开始
红
白1
白2
红
白1
白2
红
白1
白2
红
白1
白2
第一次
第二次
口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,放回搅匀,再摸出第2个球,两次摸球就可能出现3种结果:
(1)都是红球;
(2)都是白球;
(3)一红一白.
这三个事件发生的概率相等吗?
探究1
先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
由以上数状图可以看出来:
所以以上说法不正确.
2.有两双手套,形状、大小,完全相同,只有颜色不同。黑暗中,任意抽出两只配成一双的概率是多少?
解:
假设两双手套的颜色分别为红、黑,如下分析:
红1
黑1
黑2
红2
红1
黑1
黑2
红2
红1
黑1
黑2
红2
红1
黑1
黑2
红2
开始
第一次
第二次
P(配成一双)
=
=
由以上数状图可以看出来:
共有以下12种机会均等的结果:
3.下面是两个可以自由转动的转盘,每个转盘被分成了三个相等的扇形,小明和小亮用它们做配紫色(红色与蓝色能配成紫色)游戏,你认为配成紫色与配不成紫色的概率相同吗?
解:所有可能出现的结果如下:
A
红
红
蓝
(红,红)
(蓝,红)
(蓝,红)
(红,红)
(蓝,红)
(蓝,红)
(红,蓝)
(蓝,蓝)
(蓝,蓝)
B
红
蓝
蓝
一共有9种结果,每种结果出现的可能性相同,(红,蓝)能配紫色的有5种,概率为5/9;不能配紫色的有4种,概率为4/9,它们的概率不相同。
