人教版八年级上册13.4 课题学习 最短路径问题 课件(19张)
文档属性
| 名称 | 人教版八年级上册13.4 课题学习 最短路径问题 课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 684.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 18:59:59 | ||
图片预览






文档简介
(共19张PPT)
13.4
课题学习
最短路径问题
1.为什么要关于直线l的做对称点呢?
2.AM+BM为什么不是最短路径?
3.在解决两点在直线同侧问题时的一般步骤是什么?
学习难点
归纳
l
A
B
C
l
A
B
C
B′
l
A
B
C
抽象为数学模型
用旧知解决新知
利用轴对称
联想旧知
解决实
际问题
A
B
l
B
A
有A、B两个小区,现要在A、B两个小区铺设一条天然气管线,怎样铺设才使得天然气管线最短?
合作交流
探究新知
你能将这个问题抽象为数学问题吗?
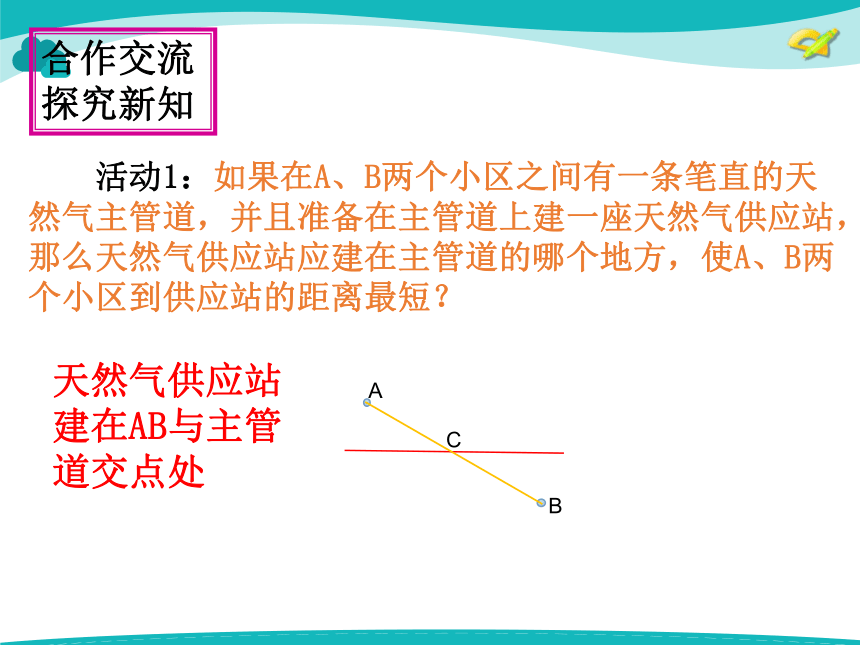
活动1:如果在A、B两个小区之间有一条笔直的天然气主管道,并且准备在主管道上建一座天然气供应站,那么天然气供应站应建在主管道的哪个地方,使A、B两个小区到供应站的距离最短?
A
B
合作交流
探究新知
C
天然气供应站建在AB与主管道交点处
活动2:如果还有一个B'小区与A小区在主管道同侧,并且B'小区与B小区刚好关于主管道对称,那么能否在主管道上找到一个点建一座天然气供应站C,使得A,B'两小区到供应站C距离之和刚好等于A,B两小区之间的距离呢?为什么?
合作交流
探究新知
A
B
B'
探究1:如果供气站建在主管道的其他任意位置,那么A,B'两小区到供气站距离之和与A,B两小区到供气站距离之和是否还相等?
合作交流
探究新知
还相等
证明:如图,在直线l上任取一点C'(与点C
不重合),连接AC',BC',B'C'.
由轴对称的性质知:
BC
=B'C,BC'=B'C'.
∴AC
+BC
=
AC
+B'C
=
AB,
AC'+BC'=
AC'+B'C'.
在△AC'B中,
AC'+BC'>AB
∴AC'+B'C'>AB,
∴当只有在C点位置时,AC+BC最短.
探究2:此时A,B'两小区到供气站距离之和与A,B两小区之间距离有怎样的关系?为什么?
合作交流
探究新知
B'
·
l
A
·
B
C
C′
探究3:在公路l同侧有A、B两个小区,现要在公路l旁修建一公交站C,要使公交站到两小区的距离之和最短,试确定公交站C的位置。
合作交流
探究新知
B
A
l
归纳新知
因此,如果在直线l同侧的两个点分别是点A,B,在l上找一个点C,使点C到点A、B距离和CA+CB最短,那么我们可以先作点B关于直线l的对称点B',连接AB’交直线l于点C,则点C即为所求。
作法:
(1)作点B
关于直线l
的对称
点B′;
(2)连接AB′,与直线l
相交
于点C.
则点C
即为所求.
B
·
l
A
·
B′
C
归纳小结
“最短路径问题”
(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.
如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.
归纳小结
“最短路径问题”
(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.
如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B',则点C是直线l与AB'的交点.
应用新知解决问题
1、如图,直线L是一条河,P、Q是两个村庄,欲在L上的某处修建一个水泵站,向P、Q两地供水,现有四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是(
)?
2.如图,AD是等边三角形△ABC的BC边上的高,AD=6,E是AD上的动点,E是AC边的中点,则EF+EC的最小值为____.
3.
如下图,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边b饮水,最后回到营地.请你设计一条放牧路线,使其所走的总路程最短。
活用新知拓展提高
1、如图,已知正方形ABCD,M是BC的中点,P是对角线BD上一动点,要使PM+PC的值最小,请确定P点的位置。
2、如图,已知菱形ABCD,M、N分别是AB、BC的中点,P是对角线AC上一动点,要使PM+PN的值最小,请确定P点的位置。
3.(造桥选址问题)如图,A和B两地在同一条河的两岸,现要在河上造一座桥MN.桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直.)
反思小结
1、知识点:
1)两点之间,线段最短
2)垂直平分线上的点到两端的的距离相等
2、思想方法:转化思想
1)将实际问题转化为数学问题,
将路程最短问题转化为线段和最小问题
2)应用轴对称性质将直线同侧两点问题转化
为异侧两点问题
1.已知如图,点A和两条直线m和n,你能在直线m、n上分别找一点P、Q,使得AP+PQ+AQ的值最小吗?
2.如果活动1中的“一条笔直的天然气主管道”变成“一条笔直的宽阔的河流”,并且准备在河上建一座桥,那么桥建在河的何处才使A小区居民通过桥到B两个小区路径最短?(假定河的两岸是平行的直线,桥要与河垂直)
?
作业布置
A
B
13.4
课题学习
最短路径问题
1.为什么要关于直线l的做对称点呢?
2.AM+BM为什么不是最短路径?
3.在解决两点在直线同侧问题时的一般步骤是什么?
学习难点
归纳
l
A
B
C
l
A
B
C
B′
l
A
B
C
抽象为数学模型
用旧知解决新知
利用轴对称
联想旧知
解决实
际问题
A
B
l
B
A
有A、B两个小区,现要在A、B两个小区铺设一条天然气管线,怎样铺设才使得天然气管线最短?
合作交流
探究新知
你能将这个问题抽象为数学问题吗?
活动1:如果在A、B两个小区之间有一条笔直的天然气主管道,并且准备在主管道上建一座天然气供应站,那么天然气供应站应建在主管道的哪个地方,使A、B两个小区到供应站的距离最短?
A
B
合作交流
探究新知
C
天然气供应站建在AB与主管道交点处
活动2:如果还有一个B'小区与A小区在主管道同侧,并且B'小区与B小区刚好关于主管道对称,那么能否在主管道上找到一个点建一座天然气供应站C,使得A,B'两小区到供应站C距离之和刚好等于A,B两小区之间的距离呢?为什么?
合作交流
探究新知
A
B
B'
探究1:如果供气站建在主管道的其他任意位置,那么A,B'两小区到供气站距离之和与A,B两小区到供气站距离之和是否还相等?
合作交流
探究新知
还相等
证明:如图,在直线l上任取一点C'(与点C
不重合),连接AC',BC',B'C'.
由轴对称的性质知:
BC
=B'C,BC'=B'C'.
∴AC
+BC
=
AC
+B'C
=
AB,
AC'+BC'=
AC'+B'C'.
在△AC'B中,
AC'+BC'>AB
∴AC'+B'C'>AB,
∴当只有在C点位置时,AC+BC最短.
探究2:此时A,B'两小区到供气站距离之和与A,B两小区之间距离有怎样的关系?为什么?
合作交流
探究新知
B'
·
l
A
·
B
C
C′
探究3:在公路l同侧有A、B两个小区,现要在公路l旁修建一公交站C,要使公交站到两小区的距离之和最短,试确定公交站C的位置。
合作交流
探究新知
B
A
l
归纳新知
因此,如果在直线l同侧的两个点分别是点A,B,在l上找一个点C,使点C到点A、B距离和CA+CB最短,那么我们可以先作点B关于直线l的对称点B',连接AB’交直线l于点C,则点C即为所求。
作法:
(1)作点B
关于直线l
的对称
点B′;
(2)连接AB′,与直线l
相交
于点C.
则点C
即为所求.
B
·
l
A
·
B′
C
归纳小结
“最短路径问题”
(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.
如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.
归纳小结
“最短路径问题”
(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.
如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B',则点C是直线l与AB'的交点.
应用新知解决问题
1、如图,直线L是一条河,P、Q是两个村庄,欲在L上的某处修建一个水泵站,向P、Q两地供水,现有四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是(
)?
2.如图,AD是等边三角形△ABC的BC边上的高,AD=6,E是AD上的动点,E是AC边的中点,则EF+EC的最小值为____.
3.
如下图,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边b饮水,最后回到营地.请你设计一条放牧路线,使其所走的总路程最短。
活用新知拓展提高
1、如图,已知正方形ABCD,M是BC的中点,P是对角线BD上一动点,要使PM+PC的值最小,请确定P点的位置。
2、如图,已知菱形ABCD,M、N分别是AB、BC的中点,P是对角线AC上一动点,要使PM+PN的值最小,请确定P点的位置。
3.(造桥选址问题)如图,A和B两地在同一条河的两岸,现要在河上造一座桥MN.桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直.)
反思小结
1、知识点:
1)两点之间,线段最短
2)垂直平分线上的点到两端的的距离相等
2、思想方法:转化思想
1)将实际问题转化为数学问题,
将路程最短问题转化为线段和最小问题
2)应用轴对称性质将直线同侧两点问题转化
为异侧两点问题
1.已知如图,点A和两条直线m和n,你能在直线m、n上分别找一点P、Q,使得AP+PQ+AQ的值最小吗?
2.如果活动1中的“一条笔直的天然气主管道”变成“一条笔直的宽阔的河流”,并且准备在河上建一座桥,那么桥建在河的何处才使A小区居民通过桥到B两个小区路径最短?(假定河的两岸是平行的直线,桥要与河垂直)
?
作业布置
A
B
