人教版七年级数学上册课件:1.2.4 绝对值(共30张PPT)
文档属性
| 名称 | 人教版七年级数学上册课件:1.2.4 绝对值(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 455.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 19:22:29 | ||
图片预览








文档简介
(共30张PPT)
绝对值
第1课时
理解绝对值的概念及性质(难点).
会求一个有理数的绝对值(重点).
1
2
学习目标
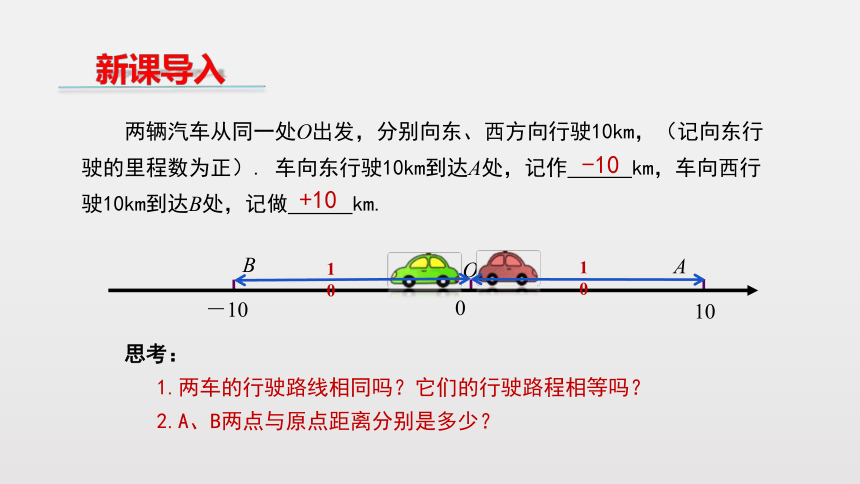
两辆汽车从同一处O出发,分别向东、西方向行驶10km,(记向东行驶的里程数为正).
车向东行驶10km到达A处,记作
km,车向西行驶10km到达B处,记做
km.
+10
-10
-10
10
0
O
B
A
新课导入
10
10
思考:
1.两车的行驶路线相同吗?它们的行驶路程相等吗?
2.A、B两点与原点距离分别是多少?
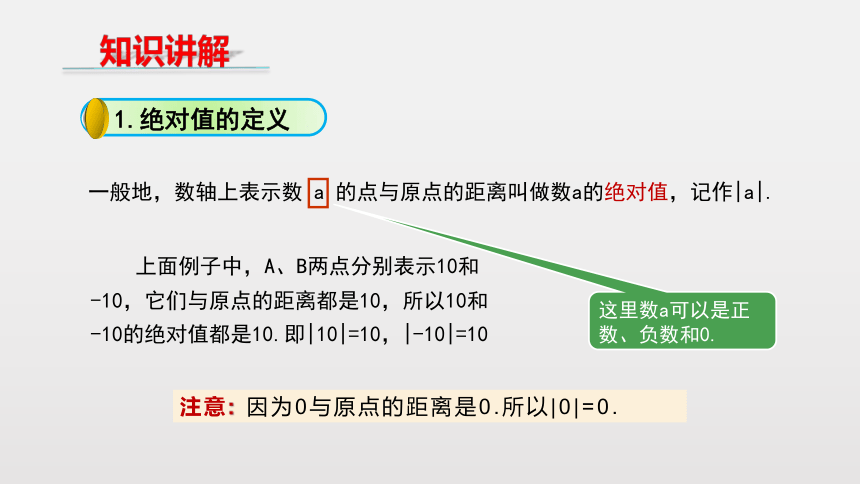
一般地,数轴上表示数
a
的点与原点的距离叫做数a的绝对值,记作|a|.
这里数a可以是正数、负数和0.
知识讲解
1.绝对值的定义
上面例子中,A、B两点分别表示10和-10,它们与原点的距离都是10,所以10和-10的绝对值都是10.即|10|=10,|-10|=10
注意:
因为0与原点的距离是0.所以|0|=0.
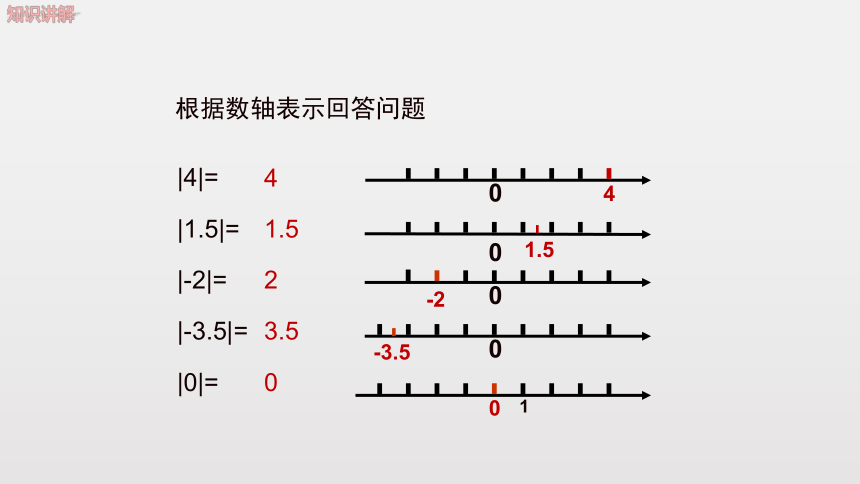
根据数轴表示回答问题
|4|=
|1.5|=
|-2|=
|-3.5|=
|0|=
0
1
0
0
0
0
4
1.5
-2
-3.5
4
1.5
2
3.5
0
知识讲解
|6|=6
|-10|=10
|0.5|=0.5
|-3|=3
|0.1|=0.1
|-1.5|=1.5
|100|=100
|-2000|=2000
|0|=0
思考:一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
观察下面等式
2.绝对值的性质
结论:
一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
知识讲解
正数的绝对值是它本身
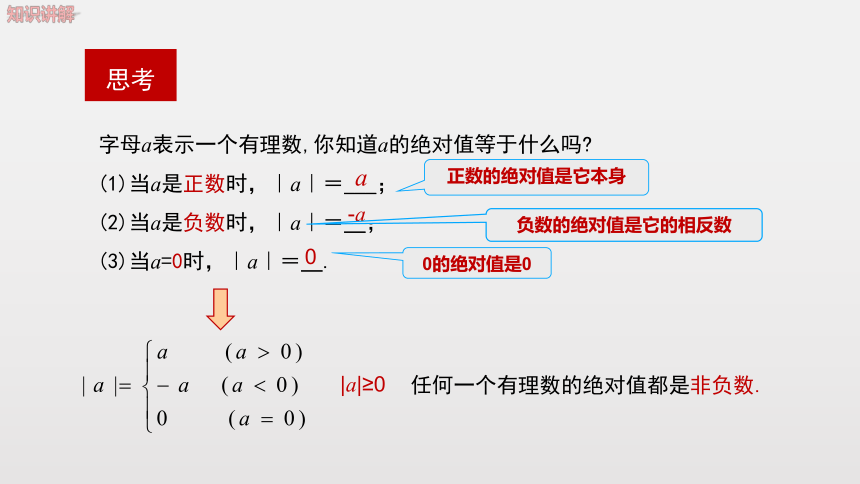
(1)当a是正数时,|a|=___;
(2)当a是负数时,|a|=_;
(3)当a=0时,|a|=_.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
字母a表示一个有理数,你知道a的绝对值等于什么吗?
|a|≥0
任何一个有理数的绝对值都是非负数.
知识讲解
思考
例1
求下列各数的绝对值.
+15,
-2.5.
解:
|+15|=15;
|-2.5|=2.5;
正数的绝对值等于它本身
负数的绝对值等于它的相反数
知识讲解
(1)绝对值等于0的是_____,
(2)绝对值等于7的正数是_____,
(3)绝对值等于7的负数是______,
(4)
3的绝对值数是___,-3的绝对值数是___.
7
-7
3
例2
填一填
归纳总结
1.绝对值相等的两个数相等或互为相反数,
2.互为相反数的两个数的绝对值相等.
3
0
知识讲解
解:根据题意可知x-3=0,y-2=0,所以x=3,y=2,故x+y=5.
归纳总结:
几个非负数的和为0,则这几个数都为0.
例3
已知|x-3|+|y-2|=0,求x+y的值
分析:
一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
知识讲解
1.判断:
(1)一个数的绝对值是9?,则这个数是9
(
)
(2)|5|=|-5|
(
)
(3)|-0.5|=|0.5|
(
)
(4)|3|>0
(
)
(5)|-1.2|>0
(
)
(6)有理数的绝对值一定是正数
(
)
(7)若a=-b,则|a|=|b|
(
)
(8)若|a|=|b|,则a=b
(
)
(9)若|a|=-a,则a必为负数
(
)
(10)互为相反数的两个数的绝对值相等
(
)
×
×
×
×
√
√
√
√
√
√
随堂训练
2.
如果a与1互为相反数,则︱a︱等于(
).
A.2
B.-2
C.1
D.-1
C
3.
―|―4|=(
)
A.―4
B.―
C.
D.4
A
4.填空:
-m
a-b
|
m|=
(m<0)
|
a
–
b
|
=
a>b)
随堂训练
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
课堂小结
一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
第2课时
掌握有理数大小的比较方法.(重点)
能利用数轴及绝对值的知识,比较两个有理数的大小.(难点)
1
2
学习目标
新课导入
珠穆朗玛峰的海拔高度为8
844.43米
吐鲁番盆地的海拔高度为-155米
哪个高呢?
根据海拔高低,
可以得出
8844.43>-155
-10℃、0℃、
6℃哪个温度高?
根据温度的高低,可以得出
-10<0,0<6.
新课导入
知识讲解
下表给出了某地未来一周中每天的最高和最低气温
星
期
一
二
三
四
五
六
日
最高气温(℃)
8
7
6
5
3
4
9
最低气温(℃)
0
1
-1
-2
-4
-3
2
其中最低的是________℃,最高的是_______℃.
你能将这七天中每天的最低气温按从低到高的顺序排列吗?
-4
9
1.借助数轴比较有理数的大小
这七天中每天的最低温度按照由低到高的顺序排列为:
-4,
-3,
-2,
-1,
0,
1,
2.
按照这个顺序排列的温度在温度计上所对应的点是
从_____到______的.
上
下
把这些数表示在数轴上,表示它们各点的顺序是
从______到______的.
左
右
思考:你能把上面的数按照这个顺序表示在数轴上吗?
-4
-3
-2
-1
0
1
2
知识讲解
数学中规定:
在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
适用于多个数的大小比较.
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
思考:
有没有最大的有理数?有没有最小的有理数?为什么?
知识讲解
例1
在数轴上表示数-4,-2,-5,2,3,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-4,-2,-5,2,3,0在数轴上表示如下图:
将它们按从小到大的顺序排列为:
-5
<-4
<-2
<0
<
2<3
-5
-4
-3
-2
-1
0
1
2
3
4
●
●
●
●
●
●
知识讲解
2.运用法则比较有理数的大小
问题
对于正数、0、负数这三类数,它们之间有什么大小关系?
用“>”或“<”号填空.
(1)3
0
(2)-2.3
0
(3)
0
0.5
(4)0
-5
(5)
-1.5
1.5
(6)4
-6
<
<
<
>
>
>
适用于一个数和0的大小比较,以及异号两数的大小比较.
法则
正数大于0,负数小于0,正数大于负数.
知识讲解
>
<
>
<
用“>”或“<”号填空,并说明理由.
(1)
2
5
(2)
-1.4
-2.5
(3)
(4)
.
两个正数,绝对值大的大;
两个负数,绝对值大的反而小.
结论
同号两数怎样比较大小呢?
同正?同负?
思考
知识讲解
例2.比较下列各数的大小.
解:先化简,-(-7)=7,
-(+4)=-4,
因为正数大于负数,所以7>-4,即
-(-7)>-(+4)
(1)-(-7)和-(+4);
异号两数比较要考虑它们的正负.
知识讲解
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两个负数,绝对值大的反而小
两个负数比较大小的一般步骤:
①求绝对值;
②比较绝对值的大小;
③比较负数的大小.
总结
知识讲解
随堂训练
1.比较下列各组数的大小
(1)2___0
,
0___-8.3
,
2.5___-90
(2)-5__-3
,
-3.14__
-
,
-7.8__-7.7
(3)-(-9)__-(+9)
,
-
[-(-0.3)]
__
-|-0.29|
>
>
>
<
<
>
>
<
2.在有理数0,│-(-
)│,-│+100│,-(-7)中最大的数是(
)
A.0
B.-(-7)
C.-│+100│
D.│-(-
)│
B
3.(成都中考)下列各数中,最大的数是(
)
(A)-2
(B)0
(C)
(D)3
4.将下列这些数用“<”连接.
0,-3,|8|,-(-1),-|-8|.
解:-|-8|<-3
<
0<
-(-1)<|8|.
D
随堂训练
5.如果a是有理数,试比较|a|与-3a的大小.
分析:由于不能确定a的正负,所以需分类讨论
解:?当a>0时,|a|>0,-3a<0,所以|a|>-3a;
?当a=0时,|a|=0,-3a=0,所以|a|=-3a;
?当a<0时,|a|=-a
>0
,-3a>0,
因为-3a>-a,所以|a|<-3a.
随堂训练
课堂小结
利用数轴
在数轴上表示的数,左边的数小于右边的数.
法则
正数大于0,0大于负数,正数大于负数;
两个负数,绝对值大的反而小.
有理数大小的比较方法
异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
绝对值
第1课时
理解绝对值的概念及性质(难点).
会求一个有理数的绝对值(重点).
1
2
学习目标
两辆汽车从同一处O出发,分别向东、西方向行驶10km,(记向东行驶的里程数为正).
车向东行驶10km到达A处,记作
km,车向西行驶10km到达B处,记做
km.
+10
-10
-10
10
0
O
B
A
新课导入
10
10
思考:
1.两车的行驶路线相同吗?它们的行驶路程相等吗?
2.A、B两点与原点距离分别是多少?
一般地,数轴上表示数
a
的点与原点的距离叫做数a的绝对值,记作|a|.
这里数a可以是正数、负数和0.
知识讲解
1.绝对值的定义
上面例子中,A、B两点分别表示10和-10,它们与原点的距离都是10,所以10和-10的绝对值都是10.即|10|=10,|-10|=10
注意:
因为0与原点的距离是0.所以|0|=0.
根据数轴表示回答问题
|4|=
|1.5|=
|-2|=
|-3.5|=
|0|=
0
1
0
0
0
0
4
1.5
-2
-3.5
4
1.5
2
3.5
0
知识讲解
|6|=6
|-10|=10
|0.5|=0.5
|-3|=3
|0.1|=0.1
|-1.5|=1.5
|100|=100
|-2000|=2000
|0|=0
思考:一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
观察下面等式
2.绝对值的性质
结论:
一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
知识讲解
正数的绝对值是它本身
(1)当a是正数时,|a|=___;
(2)当a是负数时,|a|=_;
(3)当a=0时,|a|=_.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
字母a表示一个有理数,你知道a的绝对值等于什么吗?
|a|≥0
任何一个有理数的绝对值都是非负数.
知识讲解
思考
例1
求下列各数的绝对值.
+15,
-2.5.
解:
|+15|=15;
|-2.5|=2.5;
正数的绝对值等于它本身
负数的绝对值等于它的相反数
知识讲解
(1)绝对值等于0的是_____,
(2)绝对值等于7的正数是_____,
(3)绝对值等于7的负数是______,
(4)
3的绝对值数是___,-3的绝对值数是___.
7
-7
3
例2
填一填
归纳总结
1.绝对值相等的两个数相等或互为相反数,
2.互为相反数的两个数的绝对值相等.
3
0
知识讲解
解:根据题意可知x-3=0,y-2=0,所以x=3,y=2,故x+y=5.
归纳总结:
几个非负数的和为0,则这几个数都为0.
例3
已知|x-3|+|y-2|=0,求x+y的值
分析:
一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
知识讲解
1.判断:
(1)一个数的绝对值是9?,则这个数是9
(
)
(2)|5|=|-5|
(
)
(3)|-0.5|=|0.5|
(
)
(4)|3|>0
(
)
(5)|-1.2|>0
(
)
(6)有理数的绝对值一定是正数
(
)
(7)若a=-b,则|a|=|b|
(
)
(8)若|a|=|b|,则a=b
(
)
(9)若|a|=-a,则a必为负数
(
)
(10)互为相反数的两个数的绝对值相等
(
)
×
×
×
×
√
√
√
√
√
√
随堂训练
2.
如果a与1互为相反数,则︱a︱等于(
).
A.2
B.-2
C.1
D.-1
C
3.
―|―4|=(
)
A.―4
B.―
C.
D.4
A
4.填空:
-m
a-b
|
m|=
(m<0)
|
a
–
b
|
=
a>b)
随堂训练
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
课堂小结
一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
第2课时
掌握有理数大小的比较方法.(重点)
能利用数轴及绝对值的知识,比较两个有理数的大小.(难点)
1
2
学习目标
新课导入
珠穆朗玛峰的海拔高度为8
844.43米
吐鲁番盆地的海拔高度为-155米
哪个高呢?
根据海拔高低,
可以得出
8844.43>-155
-10℃、0℃、
6℃哪个温度高?
根据温度的高低,可以得出
-10<0,0<6.
新课导入
知识讲解
下表给出了某地未来一周中每天的最高和最低气温
星
期
一
二
三
四
五
六
日
最高气温(℃)
8
7
6
5
3
4
9
最低气温(℃)
0
1
-1
-2
-4
-3
2
其中最低的是________℃,最高的是_______℃.
你能将这七天中每天的最低气温按从低到高的顺序排列吗?
-4
9
1.借助数轴比较有理数的大小
这七天中每天的最低温度按照由低到高的顺序排列为:
-4,
-3,
-2,
-1,
0,
1,
2.
按照这个顺序排列的温度在温度计上所对应的点是
从_____到______的.
上
下
把这些数表示在数轴上,表示它们各点的顺序是
从______到______的.
左
右
思考:你能把上面的数按照这个顺序表示在数轴上吗?
-4
-3
-2
-1
0
1
2
知识讲解
数学中规定:
在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
适用于多个数的大小比较.
-5
-4
-3
-2
-1
0
1
2
3
4
5
小
大
思考:
有没有最大的有理数?有没有最小的有理数?为什么?
知识讲解
例1
在数轴上表示数-4,-2,-5,2,3,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-4,-2,-5,2,3,0在数轴上表示如下图:
将它们按从小到大的顺序排列为:
-5
<-4
<-2
<0
<
2<3
-5
-4
-3
-2
-1
0
1
2
3
4
●
●
●
●
●
●
知识讲解
2.运用法则比较有理数的大小
问题
对于正数、0、负数这三类数,它们之间有什么大小关系?
用“>”或“<”号填空.
(1)3
0
(2)-2.3
0
(3)
0
0.5
(4)0
-5
(5)
-1.5
1.5
(6)4
-6
<
<
<
>
>
>
适用于一个数和0的大小比较,以及异号两数的大小比较.
法则
正数大于0,负数小于0,正数大于负数.
知识讲解
>
<
>
<
用“>”或“<”号填空,并说明理由.
(1)
2
5
(2)
-1.4
-2.5
(3)
(4)
.
两个正数,绝对值大的大;
两个负数,绝对值大的反而小.
结论
同号两数怎样比较大小呢?
同正?同负?
思考
知识讲解
例2.比较下列各数的大小.
解:先化简,-(-7)=7,
-(+4)=-4,
因为正数大于负数,所以7>-4,即
-(-7)>-(+4)
(1)-(-7)和-(+4);
异号两数比较要考虑它们的正负.
知识讲解
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两个负数,绝对值大的反而小
两个负数比较大小的一般步骤:
①求绝对值;
②比较绝对值的大小;
③比较负数的大小.
总结
知识讲解
随堂训练
1.比较下列各组数的大小
(1)2___0
,
0___-8.3
,
2.5___-90
(2)-5__-3
,
-3.14__
-
,
-7.8__-7.7
(3)-(-9)__-(+9)
,
-
[-(-0.3)]
__
-|-0.29|
>
>
>
<
<
>
>
<
2.在有理数0,│-(-
)│,-│+100│,-(-7)中最大的数是(
)
A.0
B.-(-7)
C.-│+100│
D.│-(-
)│
B
3.(成都中考)下列各数中,最大的数是(
)
(A)-2
(B)0
(C)
(D)3
4.将下列这些数用“<”连接.
0,-3,|8|,-(-1),-|-8|.
解:-|-8|<-3
<
0<
-(-1)<|8|.
D
随堂训练
5.如果a是有理数,试比较|a|与-3a的大小.
分析:由于不能确定a的正负,所以需分类讨论
解:?当a>0时,|a|>0,-3a<0,所以|a|>-3a;
?当a=0时,|a|=0,-3a=0,所以|a|=-3a;
?当a<0时,|a|=-a
>0
,-3a>0,
因为-3a>-a,所以|a|<-3a.
随堂训练
课堂小结
利用数轴
在数轴上表示的数,左边的数小于右边的数.
法则
正数大于0,0大于负数,正数大于负数;
两个负数,绝对值大的反而小.
有理数大小的比较方法
异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
