人教版数学九年级上册24.2 点和圆、直线和圆的位置关系讲义(含答案)
文档属性
| 名称 | 人教版数学九年级上册24.2 点和圆、直线和圆的位置关系讲义(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 279.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 20:15:46 | ||
图片预览




文档简介
(
与圆有关的位置关系进阶篇
)
题型一:切线的性质定理
【例1】
如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为圆心,OB为半径作半圆与BC边和AB边分别交于点D、点E,连接DE.
(1)当BD=3时,求线段DE的长;
(2)过点E作半圆O的切线,当切线与AC边相交时,设交点为F.求证:△FAE是等腰三角形.
【解答】(1)解:∵∠C=90°,AC=3,BC=4,
∴AB=5,
∵DB为直径,
∴∠DEB=∠C=90°,
又∵∠B=∠B,
∴△DBE∽△ABC,
∴,
即,
∴DE=;
(2)证法一:连接OE,
∵EF为半圆O的切线,
∴∠DEO+∠DEF=90°,
∴∠AEF=∠DEO,
∵△DBE∽△ABC,
∴∠A=∠EDB,
又∵∠EDO=∠DEO,
∴∠AEF=∠A,
∴△FAE是等腰三角形;
证法二:连接OE
∵EF为切线,
∴∠AEF+∠OEB=90°,
∵∠C=90°,
∴∠A+∠B=90°,
∵OE=OB,
∴∠OEB=∠B,
∴∠AEF=∠A,
∴△FAE是等腰三角形.
题型二:切线的判定定理
【例2】
如图△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD为半径作⊙D交AB于点E.
(1)求证:⊙D与AC相切;
(2)若AC=5,BC=3,试求AE的长.
【解答】(1)证明:过D作DF⊥AC于F,
∵∠B=90°,
∴AB⊥BC,
∵CD平分∠ACB交AB于点D,
∴BD=DF,
∴⊙D与AC相切;
(2)解:设圆的半径为x,
∵∠B=90°,BC=3,AC=5,
∴AB==4,
∵AC,BC,是圆的切线,
∴BC=CF=3,
∴AF=AB﹣CF=2,
∵AB=4,
∴AD=AB﹣BD=4﹣x,
在Rt△AFD中,(4﹣x)2=x2+22,
解得:x=,
∴AE=4﹣3=1.
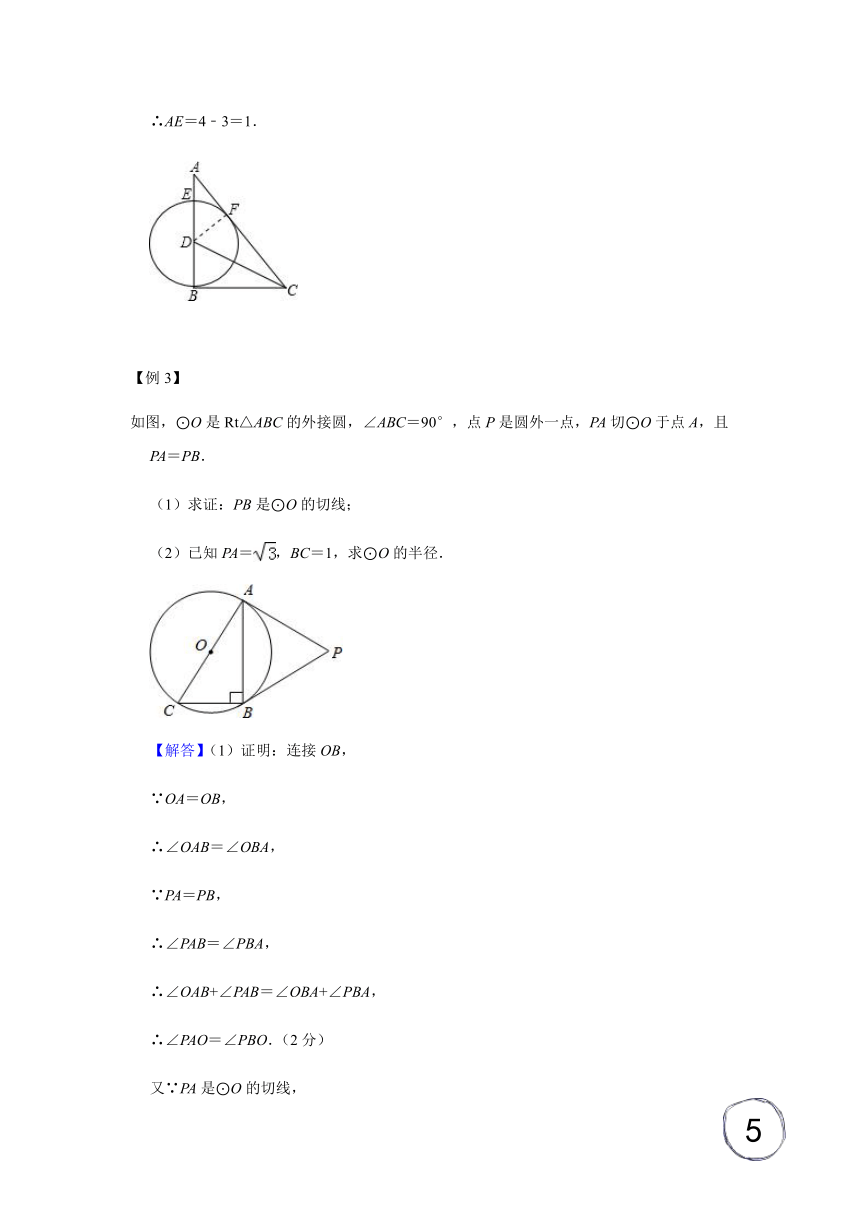
【例3】
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=,BC=1,求⊙O的半径.
【解答】(1)证明:连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵PA=PB,
∴∠PAB=∠PBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,
∴∠PAO=∠PBO.(2分)
又∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠PBO=90°,
∴OB⊥PB.(4分)
又∵OB是⊙O半径,
∴PB是⊙O的切线,(5分)
说明:还可连接OB、OP,利用△OAP≌△OBP来证明OB⊥PB.
(2)解:连接OP,交AB于点D,
∵PA=PB,
∴点P在线段AB的垂直平分线上.
∵OA=OB,
∴点O在线段AB的垂直平分线上,
∴OP垂直平分线段AB,
∴∠PDA=90°.
又∵PA切⊙O于点A,
∴∠PAO=90°,
∴∠PAO=∠PDA,
又∵∠APO=∠DPA,
∴△APO∽△DPA,
∴,
∴AP2=PO?DP.
又∵OD=BC=,
∴PO(PO﹣OD)=AP2,即PO(PO﹣)=AP2,即:PO2﹣PO=,
解得PO=2,
在Rt△APO中,,即⊙O的半径为1.
说明:求半径时,还可证明△PAO∽△ABC或在Rt△OAP中利用勾股定理.
【例4】
如图,A是以BC为直径的⊙O上一点,于点D,AD⊥BC过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
(1)求证:BF=EF;
(2)求证:PA是⊙O的切线;
(3)若FG=BF,且⊙O的半径长为,求BD和FG的长度.
【解答】(1)证明:∵BC是⊙O的直径,BE是⊙O的切线,
∴EB⊥BC.
又∵AD⊥BC,
∴AD∥BE.
∵△BFC∽△DGC,△FEC∽△GAC,
∴.
∴.
∵G是AD的中点,
∴DG=AG.
∴BF=EF.
(2)证明:连接AO,AB,
∵BC是⊙O的直径,
∴∠BAC=90°.
在Rt△BAE中,由(1),知F是斜边BE的中点,
∴AF=FB=EF.
∴∠FBA=∠FAB.
又∵OA=OB,
∴∠ABO=∠BAO.
∵BE是⊙O的切线,
∴∠EBO=90°.
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,
∴PA是⊙O的切线.
(3)解:过点F作FH⊥AD于点H,
∵BD⊥AD,FH⊥AD,
∴FH∥BC.
由(2),知∠FBA=∠BAF,
∴BF=AF.
由已知,有BF=FG,
∴AF=FG,即△AFG是等腰三角形.
∵FH⊥AD,
∴AH=GH.
∵DG=AG,
∴DG=2HG.
即.
∵FH∥BD,BF∥AD,∠FBD=90°,
∴四边形BDHF是矩形,BD=FH.
∵FH∥BC,易证△HFG∽△DCG,
∴.
即.
∵⊙O的半径长为3,
∴BC=6.
∴.
解得BD=2.
∴BD=FH=2.
∵,
∴CF=3FG.
在Rt△FBC中,
∵CF=3FG,BF=FG,
∴CF2=BF2+BC2∴(3FG)2=FG2+(6)2
解得FG=3(负值舍去)
∴FG=3.
题型三:切线长定理
切线长和切线长定理:
⑴在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长。
⑵从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
圆中的其他相关定理
1.相交弦定理
圆内的两条相交弦被交点分成的两条线段长的乘积相等。
2.
弦切角定理
⑴定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
⑵弦切角定理:弦切角等于它所夹的弧对的圆周角。
如图,PA是⊙O的切线,A是切点,AB是弦,则∠PAB=∠ACB。
3.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
4.割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
如图,PT是⊙O的切线,T是切点,PAB、PCD是割线,则PT2=PA·PB,PA·PB=PC·PD。
测试题
1.如图,直线AB与⊙O相切于点A,⊙O的半径为1,若∠OBA=30°,则OB长为( )
A.1
B.2
C.
D.2
【解答】解:∵直线AB与⊙O相切于点A,连接OA则∠OAB=90°.
∵OA=1,∴OB=.故选:B.
2.如图,PA,PB是⊙O的切线,切点分别为A,B,∠APB=50°,C是⊙O上一点,则∠ACB的度数为( )
A.50°
B.55°
C.60°
D.65°
【解答】解:连接OA,OB,
∵PA,PB是⊙O的切线,∴PA⊥OA,PB⊥OB,
∴∠AOB=360°﹣(90°+90°+50°)=130°,
∴∠ACB=∠AOB=65°.故选:D.
3.如图,PA,PB是⊙O切线,A,B为切点,C是线段AP(不包括端点)上一动点,若C由A向P运动,过C引CD与⊙O切于点E,与PB交于点D,则△PCD的周长( )
A.变大
B.变小
C.先变大再变小
D.不变
【解答】解:根据切线长定理得:PA=PB,AC=EC,BD=ED,则△PCD的周长=2PA,即△PCD的周长不变.
故选:D.
4.直角三角形的外接圆半径为5,内切圆半径为2,则此三角形周长为 24 .
【解答】解:⊙I切AB于E,切BC于F,切AC于D,连接IE,IF,ID,
则∠CDI=∠C=∠CFI=90°,ID=IF=2,
∴四边形CDIF是正方形,∴CD=CF=2,
由切线长定理得:AD=AE,BE=BF,CF=CD,
∵直角三角形的外接圆半径为5,内切圆半径为2,
∴AB=10=AE+BE=BF+AD,
即△ABC的周长是AC+BC+AB=AD+CD+CF+BF+AB=10+2+2+10=24,故答案为:24.
5.如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=( )
A.40°
B.50°
C.55°
D.60°
【解答】解:连接OC,
∵OA=OC,
∴∠A=∠OCA=25°,
∴∠DOC=2∠A=50°,
∵过点D作⊙O的切线,切点为C,
∴∠OCD=90°,
∴∠D=40°.
故选:A.
6.如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长.
【解答】解:∵AB是⊙O的切线,∴∠OBA=90°,
∵∠AOB=60°,∴∠BAO=30°,
∵OA⊥BC,BC=4,∴BD=2,
∴AB=2BD=4(cm).
7.如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.
(1)求证:CD为⊙O的切线;
(2)试探索以CD为直径的圆与AB有怎样的位置关系?证明你的结论.
【解答】(1)证明:过点O作OE⊥CD于点E,
∵在梯形ABCD中,AD∥BC,∠C=90°,
∴AD⊥CD,BC⊥CD,∴AD∥OE∥BC,
∵OA=OB,∴OE是梯形ABCD的中位线,∴OE=(AD+BC),
∵AD+BC=AB,∴OE=AB,
∵以AB为直径作⊙O.∴直线CD是⊙O的切线.
(2)设圆心为O′.过点O′作O′F⊥AB于点F,过点O′作O′M∥AD,
∴O′M是梯形ABCD的中位线,
∴O′M=(AD+BC)=AB=DM,
∴∠O′DM=∠DO′M,
∵AD∥O′M,
∴∠ADO′=∠DO′M=∠O′DM,
在△AO′D和△MO′F中,
,
∴△AO′D≌△MO′F(AAS),
∴O′F=O′A=AB,
即AB与⊙O′相切.
8.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状.
【解答】解:连结OB,如图,∵BC是⊙O的切线,
∴OB⊥BC,∴∠OBD+∠DBC=90°,
∵OA⊥OD,∴∠A+∠ODA=90°,
∵OA=OB,∴∠A=∠OBD,∴∠DBC=∠ODA,
而∠ODA=∠BDC,
∴∠DBC=∠BDC,∴△BCD为等腰三角形.
9.如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.
【解答】解:如图,连接OC,则OC是半径,
∵CE为⊙O的切线,
∴OC⊥CE.
又∵AE⊥CE,
∴AF∥OC,
∴∠BOC=∠A.
又∵AF=BF,
∴∠A=∠B,
∴∠BOC=∠B,
∴OC=BC,
∵OC=OB,
∴OC=OB=BC,即△OBC为等边三角形,则∠A=∠BOC=60°.
10.如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
(1)判断直线CD是否为⊙O的切线,请说明理由;
(2)若CD=3,求BC的长.
【解答】解:(1)CD是⊙O的切线,理由如下:
连接OD,∵∠ADE=∠A+∠C,∠C=30°,∠ADE=60°,
∴∠A=30°,
∵OA=OD,
∴∠OAD=∠ODA=30°,
又∵∠ADE=60°,
∴∠ODE=∠ODA+∠ADE=90°,
∴DC是⊙O的切线;
(2)在Rt△ODC中,∠ODC=90°,∠C=30°,CD=3,
∵tanC=,
∴OD=CD?tanC=3×=,
∴OC=2OD=2,
∵OB=OD=
∴BC=OC﹣OB=.
11.如图△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD为半径作⊙D交AB于点E.
(1)求证:⊙D与AC相切;
(2)若AC=5,BC=3,试求AE的长.
【解答】(1)证明:过D作DF⊥AC于F,
∵∠B=90°,∴AB⊥BC,
∵CD平分∠ACB交AB于点D,∴BD=DF,
∴⊙D与AC相切;
(2)解:设圆的半径为x,
∵∠B=90°,BC=3,AC=5,
∴AB==4,
∵AC,BC,是圆的切线,∴BC=CF=3,∴AF=AB﹣CF=2,
∵AB=4,∴AD=AB﹣BD=4﹣x,
在Rt△AFD中,(4﹣x)2=x2+22,
解得:x=,
∴AE=4﹣3=1.
12.在平行四边形ABCD中,AB=10,AD=m,∠D=60°,以AB为直径作⊙O.
(1)求圆心O到CD的距离(用含m的代数式来表示);
(2)当m取何值时,CD与⊙O相切.
【解答】解:(1)分别过A,O两点作AE⊥CD,OF⊥CD,垂足分别为点E,点F,
∴AE∥OF,OF就是圆心O到CD的距离.
∵四边形ABCD是平行四边形,
∴AB∥CD.
∴AE=OF.
∵在Rt△ADE中,∠D=60°,sin∠D=,
∴sin60°=.∴.∴AE=m.∴OF=AE=m.
∴圆心到CD的距离OF为m.
(2)∵OF=m,AB为⊙O的直径,且AB=10,
∴当OF=5时,CD与⊙O相切于F点,
即m=5,m=,
∴当m=时,CD与⊙O相切.
13.如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G,⊙O是△CGF的外接圆,求证:CE和⊙O相切.
【解答】证明:∵⊙O是△CGF的外接圆,O是FG的中点,∠FCG=90°,
∴OC=OG,∠OCG=∠G;
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE,
又∵∠G=∠DAE,
∴∠OCG=∠DCE;
∵∠FCO+∠OCG=90°,
∴∠FCO+∠DCE=90°,
即∠ECO=90°,
∴CE和⊙O相切.
14.如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2,BD=,则BH的长为( )
A.2
B.3
C.4
D.1
【解答】解:连接OD,
∵⊙O的直径AB,且AB⊥CD,
∴DH=CD=×2=,
∵BD=,
在Rt△BDH中,BH==1,
故选:D.
15.如图⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,若⊙O的半径为1,则CD的长为( )
A.
B.2
C.
D.1
【解答】解:连接OC,BC,∵AB是直径,∴∠ACB=90°,
∵CD是⊙O的切线,∴∠OCD=90°,
∵∠A=30°,∴∠COB=2∠A=60°,
∴CD=OC?tan∠COD=1×=.故选:A.
16.已知:如图,以△ABC的BC边为直径的半圆交AB于D,交AC于E,过E点作EF⊥BC,垂足为F,且BF:FC=5:1,AB=8,AE=2.求EC的长.
【解答】解:连接BE,则BE⊥AC.
∴BE2=AB2﹣AE2=82﹣22=60.
设FC=x,则BF=5x,BC=6x.
∵∠EFB=∠CEB,∠EBF=∠CBE,
∴△BEF∽△BCE,
∴,
∴BE2=BF?BC.
即60=5x?6x,
∵FC=x>0,
∴x=,
∴BC=6.
∵EC2=BC2﹣BE2=12,
∴EC=2.
(
17
)
与圆有关的位置关系进阶篇
)
题型一:切线的性质定理
【例1】
如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为圆心,OB为半径作半圆与BC边和AB边分别交于点D、点E,连接DE.
(1)当BD=3时,求线段DE的长;
(2)过点E作半圆O的切线,当切线与AC边相交时,设交点为F.求证:△FAE是等腰三角形.
【解答】(1)解:∵∠C=90°,AC=3,BC=4,
∴AB=5,
∵DB为直径,
∴∠DEB=∠C=90°,
又∵∠B=∠B,
∴△DBE∽△ABC,
∴,
即,
∴DE=;
(2)证法一:连接OE,
∵EF为半圆O的切线,
∴∠DEO+∠DEF=90°,
∴∠AEF=∠DEO,
∵△DBE∽△ABC,
∴∠A=∠EDB,
又∵∠EDO=∠DEO,
∴∠AEF=∠A,
∴△FAE是等腰三角形;
证法二:连接OE
∵EF为切线,
∴∠AEF+∠OEB=90°,
∵∠C=90°,
∴∠A+∠B=90°,
∵OE=OB,
∴∠OEB=∠B,
∴∠AEF=∠A,
∴△FAE是等腰三角形.
题型二:切线的判定定理
【例2】
如图△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD为半径作⊙D交AB于点E.
(1)求证:⊙D与AC相切;
(2)若AC=5,BC=3,试求AE的长.
【解答】(1)证明:过D作DF⊥AC于F,
∵∠B=90°,
∴AB⊥BC,
∵CD平分∠ACB交AB于点D,
∴BD=DF,
∴⊙D与AC相切;
(2)解:设圆的半径为x,
∵∠B=90°,BC=3,AC=5,
∴AB==4,
∵AC,BC,是圆的切线,
∴BC=CF=3,
∴AF=AB﹣CF=2,
∵AB=4,
∴AD=AB﹣BD=4﹣x,
在Rt△AFD中,(4﹣x)2=x2+22,
解得:x=,
∴AE=4﹣3=1.
【例3】
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=,BC=1,求⊙O的半径.
【解答】(1)证明:连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵PA=PB,
∴∠PAB=∠PBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,
∴∠PAO=∠PBO.(2分)
又∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠PBO=90°,
∴OB⊥PB.(4分)
又∵OB是⊙O半径,
∴PB是⊙O的切线,(5分)
说明:还可连接OB、OP,利用△OAP≌△OBP来证明OB⊥PB.
(2)解:连接OP,交AB于点D,
∵PA=PB,
∴点P在线段AB的垂直平分线上.
∵OA=OB,
∴点O在线段AB的垂直平分线上,
∴OP垂直平分线段AB,
∴∠PDA=90°.
又∵PA切⊙O于点A,
∴∠PAO=90°,
∴∠PAO=∠PDA,
又∵∠APO=∠DPA,
∴△APO∽△DPA,
∴,
∴AP2=PO?DP.
又∵OD=BC=,
∴PO(PO﹣OD)=AP2,即PO(PO﹣)=AP2,即:PO2﹣PO=,
解得PO=2,
在Rt△APO中,,即⊙O的半径为1.
说明:求半径时,还可证明△PAO∽△ABC或在Rt△OAP中利用勾股定理.
【例4】
如图,A是以BC为直径的⊙O上一点,于点D,AD⊥BC过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
(1)求证:BF=EF;
(2)求证:PA是⊙O的切线;
(3)若FG=BF,且⊙O的半径长为,求BD和FG的长度.
【解答】(1)证明:∵BC是⊙O的直径,BE是⊙O的切线,
∴EB⊥BC.
又∵AD⊥BC,
∴AD∥BE.
∵△BFC∽△DGC,△FEC∽△GAC,
∴.
∴.
∵G是AD的中点,
∴DG=AG.
∴BF=EF.
(2)证明:连接AO,AB,
∵BC是⊙O的直径,
∴∠BAC=90°.
在Rt△BAE中,由(1),知F是斜边BE的中点,
∴AF=FB=EF.
∴∠FBA=∠FAB.
又∵OA=OB,
∴∠ABO=∠BAO.
∵BE是⊙O的切线,
∴∠EBO=90°.
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,
∴PA是⊙O的切线.
(3)解:过点F作FH⊥AD于点H,
∵BD⊥AD,FH⊥AD,
∴FH∥BC.
由(2),知∠FBA=∠BAF,
∴BF=AF.
由已知,有BF=FG,
∴AF=FG,即△AFG是等腰三角形.
∵FH⊥AD,
∴AH=GH.
∵DG=AG,
∴DG=2HG.
即.
∵FH∥BD,BF∥AD,∠FBD=90°,
∴四边形BDHF是矩形,BD=FH.
∵FH∥BC,易证△HFG∽△DCG,
∴.
即.
∵⊙O的半径长为3,
∴BC=6.
∴.
解得BD=2.
∴BD=FH=2.
∵,
∴CF=3FG.
在Rt△FBC中,
∵CF=3FG,BF=FG,
∴CF2=BF2+BC2∴(3FG)2=FG2+(6)2
解得FG=3(负值舍去)
∴FG=3.
题型三:切线长定理
切线长和切线长定理:
⑴在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长。
⑵从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
圆中的其他相关定理
1.相交弦定理
圆内的两条相交弦被交点分成的两条线段长的乘积相等。
2.
弦切角定理
⑴定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
⑵弦切角定理:弦切角等于它所夹的弧对的圆周角。
如图,PA是⊙O的切线,A是切点,AB是弦,则∠PAB=∠ACB。
3.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
4.割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
如图,PT是⊙O的切线,T是切点,PAB、PCD是割线,则PT2=PA·PB,PA·PB=PC·PD。
测试题
1.如图,直线AB与⊙O相切于点A,⊙O的半径为1,若∠OBA=30°,则OB长为( )
A.1
B.2
C.
D.2
【解答】解:∵直线AB与⊙O相切于点A,连接OA则∠OAB=90°.
∵OA=1,∴OB=.故选:B.
2.如图,PA,PB是⊙O的切线,切点分别为A,B,∠APB=50°,C是⊙O上一点,则∠ACB的度数为( )
A.50°
B.55°
C.60°
D.65°
【解答】解:连接OA,OB,
∵PA,PB是⊙O的切线,∴PA⊥OA,PB⊥OB,
∴∠AOB=360°﹣(90°+90°+50°)=130°,
∴∠ACB=∠AOB=65°.故选:D.
3.如图,PA,PB是⊙O切线,A,B为切点,C是线段AP(不包括端点)上一动点,若C由A向P运动,过C引CD与⊙O切于点E,与PB交于点D,则△PCD的周长( )
A.变大
B.变小
C.先变大再变小
D.不变
【解答】解:根据切线长定理得:PA=PB,AC=EC,BD=ED,则△PCD的周长=2PA,即△PCD的周长不变.
故选:D.
4.直角三角形的外接圆半径为5,内切圆半径为2,则此三角形周长为 24 .
【解答】解:⊙I切AB于E,切BC于F,切AC于D,连接IE,IF,ID,
则∠CDI=∠C=∠CFI=90°,ID=IF=2,
∴四边形CDIF是正方形,∴CD=CF=2,
由切线长定理得:AD=AE,BE=BF,CF=CD,
∵直角三角形的外接圆半径为5,内切圆半径为2,
∴AB=10=AE+BE=BF+AD,
即△ABC的周长是AC+BC+AB=AD+CD+CF+BF+AB=10+2+2+10=24,故答案为:24.
5.如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=( )
A.40°
B.50°
C.55°
D.60°
【解答】解:连接OC,
∵OA=OC,
∴∠A=∠OCA=25°,
∴∠DOC=2∠A=50°,
∵过点D作⊙O的切线,切点为C,
∴∠OCD=90°,
∴∠D=40°.
故选:A.
6.如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长.
【解答】解:∵AB是⊙O的切线,∴∠OBA=90°,
∵∠AOB=60°,∴∠BAO=30°,
∵OA⊥BC,BC=4,∴BD=2,
∴AB=2BD=4(cm).
7.如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.
(1)求证:CD为⊙O的切线;
(2)试探索以CD为直径的圆与AB有怎样的位置关系?证明你的结论.
【解答】(1)证明:过点O作OE⊥CD于点E,
∵在梯形ABCD中,AD∥BC,∠C=90°,
∴AD⊥CD,BC⊥CD,∴AD∥OE∥BC,
∵OA=OB,∴OE是梯形ABCD的中位线,∴OE=(AD+BC),
∵AD+BC=AB,∴OE=AB,
∵以AB为直径作⊙O.∴直线CD是⊙O的切线.
(2)设圆心为O′.过点O′作O′F⊥AB于点F,过点O′作O′M∥AD,
∴O′M是梯形ABCD的中位线,
∴O′M=(AD+BC)=AB=DM,
∴∠O′DM=∠DO′M,
∵AD∥O′M,
∴∠ADO′=∠DO′M=∠O′DM,
在△AO′D和△MO′F中,
,
∴△AO′D≌△MO′F(AAS),
∴O′F=O′A=AB,
即AB与⊙O′相切.
8.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状.
【解答】解:连结OB,如图,∵BC是⊙O的切线,
∴OB⊥BC,∴∠OBD+∠DBC=90°,
∵OA⊥OD,∴∠A+∠ODA=90°,
∵OA=OB,∴∠A=∠OBD,∴∠DBC=∠ODA,
而∠ODA=∠BDC,
∴∠DBC=∠BDC,∴△BCD为等腰三角形.
9.如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.
【解答】解:如图,连接OC,则OC是半径,
∵CE为⊙O的切线,
∴OC⊥CE.
又∵AE⊥CE,
∴AF∥OC,
∴∠BOC=∠A.
又∵AF=BF,
∴∠A=∠B,
∴∠BOC=∠B,
∴OC=BC,
∵OC=OB,
∴OC=OB=BC,即△OBC为等边三角形,则∠A=∠BOC=60°.
10.如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
(1)判断直线CD是否为⊙O的切线,请说明理由;
(2)若CD=3,求BC的长.
【解答】解:(1)CD是⊙O的切线,理由如下:
连接OD,∵∠ADE=∠A+∠C,∠C=30°,∠ADE=60°,
∴∠A=30°,
∵OA=OD,
∴∠OAD=∠ODA=30°,
又∵∠ADE=60°,
∴∠ODE=∠ODA+∠ADE=90°,
∴DC是⊙O的切线;
(2)在Rt△ODC中,∠ODC=90°,∠C=30°,CD=3,
∵tanC=,
∴OD=CD?tanC=3×=,
∴OC=2OD=2,
∵OB=OD=
∴BC=OC﹣OB=.
11.如图△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD为半径作⊙D交AB于点E.
(1)求证:⊙D与AC相切;
(2)若AC=5,BC=3,试求AE的长.
【解答】(1)证明:过D作DF⊥AC于F,
∵∠B=90°,∴AB⊥BC,
∵CD平分∠ACB交AB于点D,∴BD=DF,
∴⊙D与AC相切;
(2)解:设圆的半径为x,
∵∠B=90°,BC=3,AC=5,
∴AB==4,
∵AC,BC,是圆的切线,∴BC=CF=3,∴AF=AB﹣CF=2,
∵AB=4,∴AD=AB﹣BD=4﹣x,
在Rt△AFD中,(4﹣x)2=x2+22,
解得:x=,
∴AE=4﹣3=1.
12.在平行四边形ABCD中,AB=10,AD=m,∠D=60°,以AB为直径作⊙O.
(1)求圆心O到CD的距离(用含m的代数式来表示);
(2)当m取何值时,CD与⊙O相切.
【解答】解:(1)分别过A,O两点作AE⊥CD,OF⊥CD,垂足分别为点E,点F,
∴AE∥OF,OF就是圆心O到CD的距离.
∵四边形ABCD是平行四边形,
∴AB∥CD.
∴AE=OF.
∵在Rt△ADE中,∠D=60°,sin∠D=,
∴sin60°=.∴.∴AE=m.∴OF=AE=m.
∴圆心到CD的距离OF为m.
(2)∵OF=m,AB为⊙O的直径,且AB=10,
∴当OF=5时,CD与⊙O相切于F点,
即m=5,m=,
∴当m=时,CD与⊙O相切.
13.如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G,⊙O是△CGF的外接圆,求证:CE和⊙O相切.
【解答】证明:∵⊙O是△CGF的外接圆,O是FG的中点,∠FCG=90°,
∴OC=OG,∠OCG=∠G;
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE,
又∵∠G=∠DAE,
∴∠OCG=∠DCE;
∵∠FCO+∠OCG=90°,
∴∠FCO+∠DCE=90°,
即∠ECO=90°,
∴CE和⊙O相切.
14.如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2,BD=,则BH的长为( )
A.2
B.3
C.4
D.1
【解答】解:连接OD,
∵⊙O的直径AB,且AB⊥CD,
∴DH=CD=×2=,
∵BD=,
在Rt△BDH中,BH==1,
故选:D.
15.如图⊙O的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,若⊙O的半径为1,则CD的长为( )
A.
B.2
C.
D.1
【解答】解:连接OC,BC,∵AB是直径,∴∠ACB=90°,
∵CD是⊙O的切线,∴∠OCD=90°,
∵∠A=30°,∴∠COB=2∠A=60°,
∴CD=OC?tan∠COD=1×=.故选:A.
16.已知:如图,以△ABC的BC边为直径的半圆交AB于D,交AC于E,过E点作EF⊥BC,垂足为F,且BF:FC=5:1,AB=8,AE=2.求EC的长.
【解答】解:连接BE,则BE⊥AC.
∴BE2=AB2﹣AE2=82﹣22=60.
设FC=x,则BF=5x,BC=6x.
∵∠EFB=∠CEB,∠EBF=∠CBE,
∴△BEF∽△BCE,
∴,
∴BE2=BF?BC.
即60=5x?6x,
∵FC=x>0,
∴x=,
∴BC=6.
∵EC2=BC2﹣BE2=12,
∴EC=2.
(
17
)
同课章节目录
