2020-2021学年苏科新版九年级下册数学《第6章 图形的相似》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科新版九年级下册数学《第6章 图形的相似》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 398.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 22:25:07 | ||
图片预览



文档简介
2020-2021学年苏科新版九年级下册数学《第6章
图形的相似》单元测试卷
一.选择题
1.已知线段a=10cm,b=25cm,则的值为( )
A.
B.
C.
D.2
2.如图,在△ABC中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是( )
A.∠ADE=∠C
B.∠AED=∠B
C.=
D.=
3.如果3x=4y(y≠0),那么下列比例式中成立的是( )
A.
B.
C.
D.
4.已知点C是线段AB的黄金分割点,且AC>BC,AB=200,则AC的长度是( )
A.200(﹣1)
B.100(﹣1)
C.100(3﹣)
D.50(﹣1)
5.如图,AB∥CD∥EF,若BF=3DF,则的值是( )
A.
B.2
C.
D.3
6.下列各选项中的两个图形不一定相似的是( )
A.两个斜边不等的等腰直角三角形
B.两个边长不等的菱形
C.两个边长不等的等边三角形
D.两个边长不等的正方形
7.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm
B.60cm,100cm
C.75cm,115cm
D.85cm,125cm
8.如图,在△ABC中,AB=AC=10,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=3,则点F到BC的距离为( )
A.3
B.2
C.
D.
9.如图,在平面直角坐标系中,已知点A(﹣2,1),B(﹣1,2),以原点O为位似中心,相似比为2,把△ABO放大,则点B的对应点B′的坐标是( )
A.(﹣4,2)
B.(﹣2,4)
C.(﹣4,2)或(﹣2,4)
D.(﹣2,4)或(2,﹣4)
10.如图,在△ABC,AB=AC=a,点D是边BC上的一点,且BD=a,AD=DC=1,则a等于( )
A.
B.
C.1
D.2
二.填空题
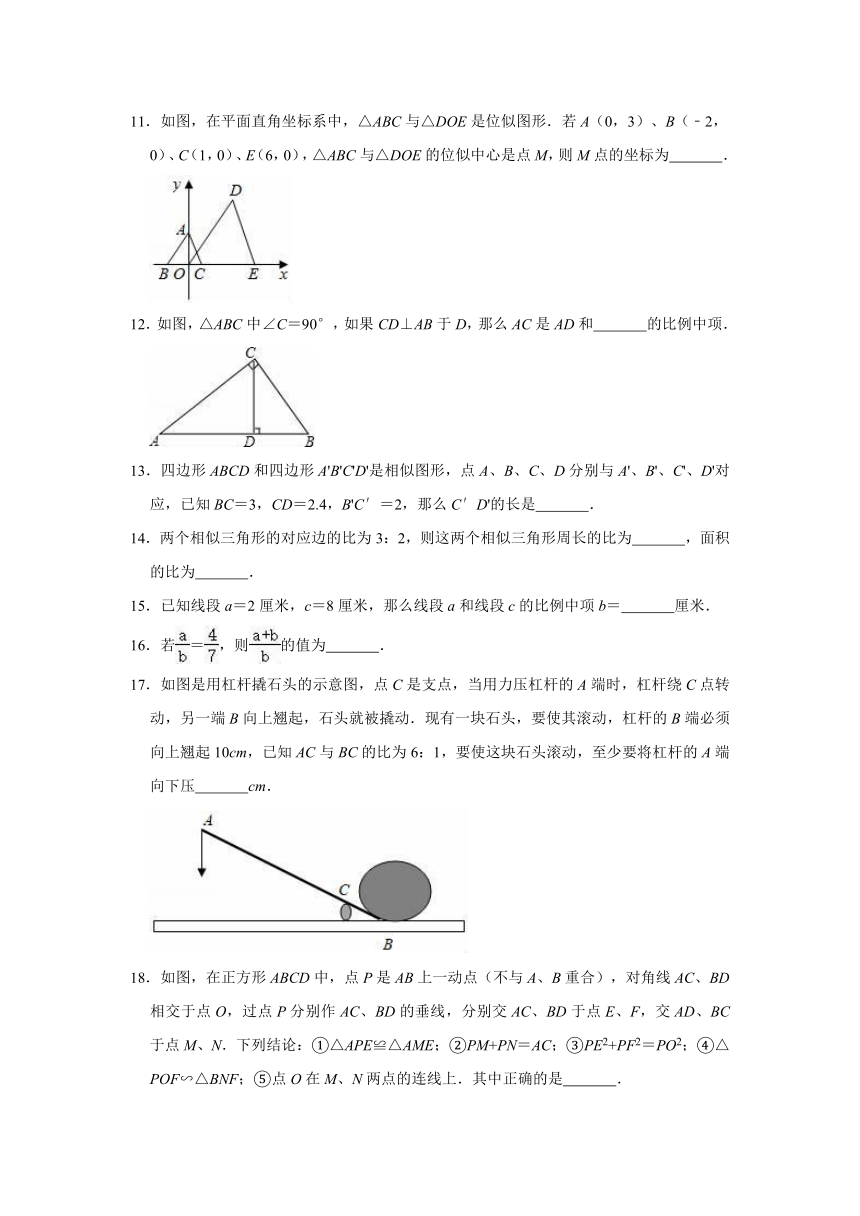
11.如图,在平面直角坐标系中,△ABC与△DOE是位似图形.若A(0,3)、B(﹣2,
0)、C(1,0)、E(6,0),△ABC与△DOE的位似中心是点M,则M点的坐标为
.
12.如图,△ABC中∠C=90°,如果CD⊥AB于D,那么AC是AD和
的比例中项.
13.四边形ABCD和四边形A'B'C'D'是相似图形,点A、B、C、D分别与A'、B'、C'、D'对应,已知BC=3,CD=2.4,B'C′=2,那么C′D'的长是
.
14.两个相似三角形的对应边的比为3:2,则这两个相似三角形周长的比为
,面积的比为
.
15.已知线段a=2厘米,c=8厘米,那么线段a和线段c的比例中项b=
厘米.
16.若=,则的值为
.
17.如图是用杠杆撬石头的示意图,点C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起10cm,已知AC与BC的比为6:1,要使这块石头滚动,至少要将杠杆的A端向下压
cm.
18.如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是
.
19.已知△ABC,P是边AB上的一点,连接CP,请你添加一个条件,使△ACP∽△ABC,这个条件可以是
.(写出一个即可)
20.如图,在平行四边形ABCD中,点E是边BC上的黄金分割点,且BE>CE,AE与BD相交于点F.那么FD:BF的值为
.
三.解答题
21.已知a:b:c=3:2:1,且2a﹣3b+c=10,求a+2b﹣3c的值.
22.如图,在边长为1个单位长度的小正方形网格中,
(1)画出△ABC向上平移6个单位,再向右平移5个单位后的△A1B1C1;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2BC2,请在网格中画出△A2BC2;
(3)直接写出△CC1C2的面积,及A1,A2的坐标.
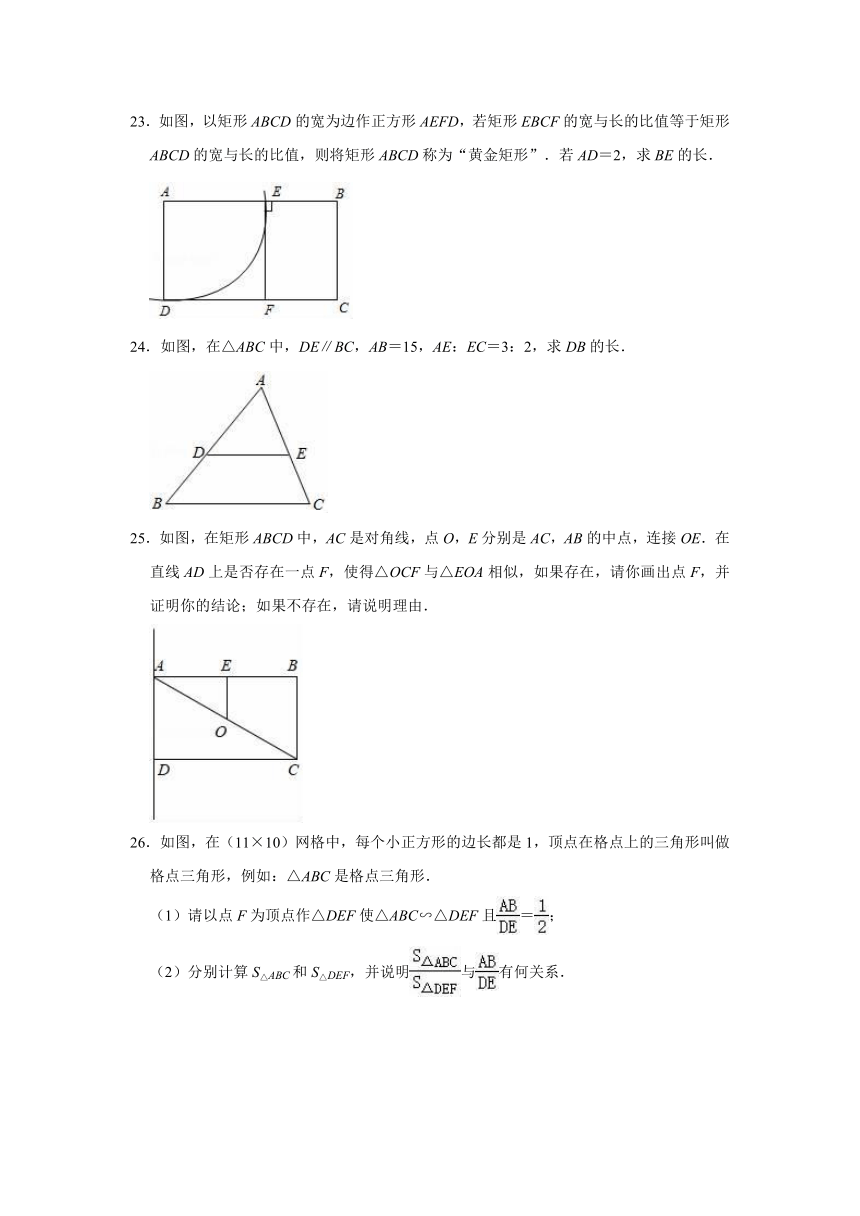
23.如图,以矩形ABCD的宽为边作正方形AEFD,若矩形EBCF的宽与长的比值等于矩形ABCD的宽与长的比值,则将矩形ABCD称为“黄金矩形”.若AD=2,求BE的长.
24.如图,在△ABC中,DE∥BC,AB=15,AE:EC=3:2,求DB的长.
25.如图,在矩形ABCD中,AC是对角线,点O,E分别是AC,AB的中点,连接OE.在直线AD上是否存在一点F,使得△OCF与△EOA相似,如果存在,请你画出点F,并证明你的结论;如果不存在,请说明理由.
26.如图,在(11×10)网格中,每个小正方形的边长都是1,顶点在格点上的三角形叫做格点三角形,例如:△ABC是格点三角形.
(1)请以点F为顶点作△DEF使△ABC∽△DEF且=;
(2)分别计算S△ABC和S△DEF,并说明与有何关系.
27.如图,点E是矩形ABCD的边AB的中点,F是BC边上一动点,线段DE和AF相交于点P,连接PC,过A作AQ∥PC交PD于点Q.
(1)证明:PC=2AQ;
(2)已知AD2=PD?DE,AB=10,AD=12,求BF的长;
(3)当点F为BC的中点时,求的值.
参考答案与试题解析
一.选择题
1.解:∵a=10cm,b=25cm,
∴==.
故选:C.
2.解:∵∠DAE=∠CAB,
∴当∠ADE=∠C时,△ADE∽△ACB;
当∠AED=∠B时,△ADE∽△ACB;
当=时,△ADE∽△ACB.
故选:C.
3.解:A、由比例的性质,得3x=4y与3x=4y一致,故A符合题意;
B、由比例的性质,得4x=3y与3x=4y不一致,故B不符合题意;
C、由比例的性质,得4x=3y与3x=4y不一致,故C不符合题意;
D、由比例的性质,得xy=12与3x=4y不一致,故D不符合题意.
故选:A.
4.解:∵点C是线段AB的黄金分割点,且AC>BC,
∴AC=AB,
而AB=200,
∴AC=×200=100(﹣1).
故选:B.
5.解:∵AB∥CD∥EF,
∴,
故选:B.
6.解:A、两个斜边不等的等腰直角三角形一定相似,不符合题意;
B、两个边长不等的菱形的对应角不一定相等,故两个菱形不一定相似,符合题意;
C、两个边长不等的等边三角形一定相似,不符合题意;
D、两个边长不等的正方形一定相似,不符合题意,
故选:B.
7.解:根据题意两个三角形的相似比是15:23,周长比就是15:23,
大小周长相差8份,所以每份的周长是40÷8=5cm,
所以两个三角形的周长分别为5×15=75cm,5×23=115cm.
故选:C.
8.解:过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H,
∵AB=AC,AD=AG,
∴AD:AB=AG:AC,
∵∠BAC=∠DAG,
∴△ADG∽△ABC,
∴∠ADG=∠B,
∴DG∥BC,
∵四边形DEFG是正方形,
∴FG⊥DG,
∴FH⊥BC,AN⊥DG,
∵AB=AC=10,BC=12,
∴BM=BC=6,
∴AM===8,
∵DG∥BC,
∴△ADG∽△ABC,
∴,
∴,
∴AN=2,
∴MN=AM﹣AN=6,
∴FH=MN﹣GF=6﹣3=3,
故选:A.
9.解:∵以原点O为位似中心,相似比为2,将△OAB放大为△OA′B′,点B(﹣1,2),
∴B′点的坐标为(﹣2,4)或(2,﹣4).
故选:D.
10.解:∵AB=AC,
∴∠B=∠C,
∵DA=DC,
∴∠DAC=∠C,
∴∠DAC=∠B,
∵∠C=∠C,
∴△CDA∽△CAB,
∴=,
∴CA2=CD?CB,
∵CA=a,BD=a,CD=1,
∴CB=1+a,
∴a2=1?(1+a),
∴a2﹣a﹣1=0,
∴a=或(舍弃),
故选:A.
二.填空题
11.解:过点D作DH⊥OE于点H,
由题意可得:BC=3,OE=6,△ABC∽△DOE,
则位似比为:3:6=1:2,
故OH=2OB=4,DH=2OA=6,
则D点的坐标为:(4,6),
由MO:MH=1:2,
MH=MO+4,
故MO:(MO+4)=1:2,
解得:MO=4,
则M点坐标为:(﹣4,0).
故答案为:(﹣4,0).
12.解:∵∠C=90°,CD⊥AB,
∴AC2=AD?AB,
∴AC是AD和AB的比例中项,
故答案为:AB.
13.解:∵四边形ABCD∽四边形A'B'C'D',
∴CD:C′D′=BC:B′C′,
∵BC=3,CD=2.4,B'C′=2,
∴C′D′=1.6,
故答案为:1.6.
14.解:∵两个相似三角形的相似比为3:2,
∴它们对应周长的比为3:2;
对应面积的比是(3:2)2=9:4.
故答案为:3:2;9:4.
15.解:∵线段b是a、c的比例中项,
∴b2=ac=16,
解得:b=±4,
又∵线段是正数,
∴b=4(厘米).
故答案为:4.
16.解:∵=,
∴=+1=+1=.
故答案为:.
17.解:如图,AM、BN都与水平线的垂直,M,N是垂足,则AM∥BN,
∵AM∥BN,
∴△ACM∽△BCN,
∴=,
∵AC与BC之比为6:1,
∴==6,即AM=6BN,
∴当BN≥10cm时,AM≥60cm,
故要使这块石头滚动,至少要将杠杆的A端向下压60cm.
故答案为:60.
18.解:①∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,
∵PM⊥AC,
∴∠AEP=∠AEM=90°,
在△APE和△AME中,
,
∴△APE≌△AME(ASA),
故①正确;
②∵△APE≌△AME,
∴PE=EM=PM,
同理,FP=FN=NP,
∵正方形ABCD中,AC⊥BD,
又∵PE⊥AC,PF⊥BD,
∴∠PEO=∠EOF=∠PFO=90°,且△APE中AE=PE
∴四边形PEOF是矩形.
∴PF=OE,
在△APE中,∠AEP=90°,∠PAE=45°,
∴△APE为等腰直角三角形,
∴AE=PE,
∴PE+PF=OA,
又∵PE=EM=PM,FP=FN=NP,OA=AC,
∴PM+PN=AC,
故②正确;
③∵四边形PEOF是矩形,
∴PE=OF,
在直角△OPF中,OF2+PF2=PO2,
∴PE2+PF2=PO2,
故③正确;
④∵△APE≌△AME,
∴AP=AM
△BNF是等腰直角三角形,而△POF不一定是,
∴△POF与△BNF不一定相似,
故④错误;
⑤∵△APE≌△AME,
∴ME=PE,
∴AE是MP是中垂线,
∴MO=OP,
又∵OE⊥MP,
∴∠MOE=∠POE,
同理可证∠POF=∠NOF,
∵∠POE+∠POF=∠EOF=90°,
∴∠MOE+∠POE+∠POF+∠NOF=180°,
∴点M,点O,点N三点共线,
故⑤正确,
故答案为①②③⑤.
19.解:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB或=时,△ACP∽△ABC,
故答案为:∠ACP=∠B,或∠APC=∠ACB或=.
20.解:∵点E是边BC上的黄金分割点,且BE>CE,
∴BE=BC,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BE,
∴△EBF∽△ADF,
∴==,
∴=,
故答案为.
三.解答题
21.解:设a=3k,b=2k,c=k,
∵2a﹣3b+c=10,
∴6k﹣6k+k=10,
∴k=10,
∴a=30,b=20,c=10,
∴a+2b﹣3c=30+40﹣30=40.
22.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2BC2为所作;
(3)△CC1C2的面积=×3×6=9;
A1的坐标为(7,9);A2的坐标为(3,5).
23.解:∵四边形AEFD是正方形,
∴AE=AD=2,
∵矩形ABCD为黄金矩形,
∴AD=AB,
即2=AB,
解得:AB=+1,
∴BE=AB﹣AE=+1﹣2=﹣1.
24.解:∵DE∥BC,
∴,
又∵AE:EC=3:2,
∴,
∴,
又∵AB=15,
∴,
解得:BD=6.
25.解:存在,如图,点F即为所求.
理由:∵OA=OC,OF⊥AC,
∴FA=FC,
∴∠AFO=∠CFO,
∵∠BAD=∠AOF=90°,
∴∠EAO+∠FAO=90°,∠FAO+∠AFO=90°,
∴∠EAO=∠AFO=∠CFO,
∵AE=EB,AO=OC,
∴OE∥BC,
∴∠AEO=∠B=90°,
∴∠AEO=∠FOC=90°,
∴△CFO∽△CAE.
26.解:(1)如图,△DEF即为所求.
(2)S△ABC=×3×1=,S△DEF=×6×2=6,AB=,DE=2,
∴=()2,
27.证明:(1)∵AQ∥PC,
∴∠AQE=∠CPD,
由题意知,AE∥CD,,
∴∠AEQ=∠CDP,
∴ΔAEQ∽ΔCDP,
∴,
∴PC=2AQ;
(2)∵AD2=PD?DE,
即,
∵∠ADP=∠EDA,
∴ΔADP∽ΔEDA,
∴∠DAP=∠DEA,
∵AD∥BC,
∴∠DAP=∠AFB,
∴∠DEA=∠AFB,
在矩形ABCD中,∠DAE=∠ABF=90°,
∴ΔDAE∽ΔABF,
∴,即,
∴;
(3)如图,延长DE交CB的延长线于点G,
∵点E是AB的中点,
∴AE=BE,
∵AD∥BC,
∴∠ADE=∠BGE,
∵∠AED=∠BEG,
∴ΔADE≌ΔBGE(AAS),
∴AD=BG,
又AD=BC,
∴GC=BG+BC=2AD,
又点F为BC的中点,
∴BC=2BF,
∴AD=2BF,BG=2BF,
∴GF=BG+BF=3BF,
∴,
由题意知,AD∥GC,
∴ΔAPD∽ΔFPG,
∴.
图形的相似》单元测试卷
一.选择题
1.已知线段a=10cm,b=25cm,则的值为( )
A.
B.
C.
D.2
2.如图,在△ABC中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是( )
A.∠ADE=∠C
B.∠AED=∠B
C.=
D.=
3.如果3x=4y(y≠0),那么下列比例式中成立的是( )
A.
B.
C.
D.
4.已知点C是线段AB的黄金分割点,且AC>BC,AB=200,则AC的长度是( )
A.200(﹣1)
B.100(﹣1)
C.100(3﹣)
D.50(﹣1)
5.如图,AB∥CD∥EF,若BF=3DF,则的值是( )
A.
B.2
C.
D.3
6.下列各选项中的两个图形不一定相似的是( )
A.两个斜边不等的等腰直角三角形
B.两个边长不等的菱形
C.两个边长不等的等边三角形
D.两个边长不等的正方形
7.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm
B.60cm,100cm
C.75cm,115cm
D.85cm,125cm
8.如图,在△ABC中,AB=AC=10,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=3,则点F到BC的距离为( )
A.3
B.2
C.
D.
9.如图,在平面直角坐标系中,已知点A(﹣2,1),B(﹣1,2),以原点O为位似中心,相似比为2,把△ABO放大,则点B的对应点B′的坐标是( )
A.(﹣4,2)
B.(﹣2,4)
C.(﹣4,2)或(﹣2,4)
D.(﹣2,4)或(2,﹣4)
10.如图,在△ABC,AB=AC=a,点D是边BC上的一点,且BD=a,AD=DC=1,则a等于( )
A.
B.
C.1
D.2
二.填空题
11.如图,在平面直角坐标系中,△ABC与△DOE是位似图形.若A(0,3)、B(﹣2,
0)、C(1,0)、E(6,0),△ABC与△DOE的位似中心是点M,则M点的坐标为
.
12.如图,△ABC中∠C=90°,如果CD⊥AB于D,那么AC是AD和
的比例中项.
13.四边形ABCD和四边形A'B'C'D'是相似图形,点A、B、C、D分别与A'、B'、C'、D'对应,已知BC=3,CD=2.4,B'C′=2,那么C′D'的长是
.
14.两个相似三角形的对应边的比为3:2,则这两个相似三角形周长的比为
,面积的比为
.
15.已知线段a=2厘米,c=8厘米,那么线段a和线段c的比例中项b=
厘米.
16.若=,则的值为
.
17.如图是用杠杆撬石头的示意图,点C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起10cm,已知AC与BC的比为6:1,要使这块石头滚动,至少要将杠杆的A端向下压
cm.
18.如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是
.
19.已知△ABC,P是边AB上的一点,连接CP,请你添加一个条件,使△ACP∽△ABC,这个条件可以是
.(写出一个即可)
20.如图,在平行四边形ABCD中,点E是边BC上的黄金分割点,且BE>CE,AE与BD相交于点F.那么FD:BF的值为
.
三.解答题
21.已知a:b:c=3:2:1,且2a﹣3b+c=10,求a+2b﹣3c的值.
22.如图,在边长为1个单位长度的小正方形网格中,
(1)画出△ABC向上平移6个单位,再向右平移5个单位后的△A1B1C1;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2BC2,请在网格中画出△A2BC2;
(3)直接写出△CC1C2的面积,及A1,A2的坐标.
23.如图,以矩形ABCD的宽为边作正方形AEFD,若矩形EBCF的宽与长的比值等于矩形ABCD的宽与长的比值,则将矩形ABCD称为“黄金矩形”.若AD=2,求BE的长.
24.如图,在△ABC中,DE∥BC,AB=15,AE:EC=3:2,求DB的长.
25.如图,在矩形ABCD中,AC是对角线,点O,E分别是AC,AB的中点,连接OE.在直线AD上是否存在一点F,使得△OCF与△EOA相似,如果存在,请你画出点F,并证明你的结论;如果不存在,请说明理由.
26.如图,在(11×10)网格中,每个小正方形的边长都是1,顶点在格点上的三角形叫做格点三角形,例如:△ABC是格点三角形.
(1)请以点F为顶点作△DEF使△ABC∽△DEF且=;
(2)分别计算S△ABC和S△DEF,并说明与有何关系.
27.如图,点E是矩形ABCD的边AB的中点,F是BC边上一动点,线段DE和AF相交于点P,连接PC,过A作AQ∥PC交PD于点Q.
(1)证明:PC=2AQ;
(2)已知AD2=PD?DE,AB=10,AD=12,求BF的长;
(3)当点F为BC的中点时,求的值.
参考答案与试题解析
一.选择题
1.解:∵a=10cm,b=25cm,
∴==.
故选:C.
2.解:∵∠DAE=∠CAB,
∴当∠ADE=∠C时,△ADE∽△ACB;
当∠AED=∠B时,△ADE∽△ACB;
当=时,△ADE∽△ACB.
故选:C.
3.解:A、由比例的性质,得3x=4y与3x=4y一致,故A符合题意;
B、由比例的性质,得4x=3y与3x=4y不一致,故B不符合题意;
C、由比例的性质,得4x=3y与3x=4y不一致,故C不符合题意;
D、由比例的性质,得xy=12与3x=4y不一致,故D不符合题意.
故选:A.
4.解:∵点C是线段AB的黄金分割点,且AC>BC,
∴AC=AB,
而AB=200,
∴AC=×200=100(﹣1).
故选:B.
5.解:∵AB∥CD∥EF,
∴,
故选:B.
6.解:A、两个斜边不等的等腰直角三角形一定相似,不符合题意;
B、两个边长不等的菱形的对应角不一定相等,故两个菱形不一定相似,符合题意;
C、两个边长不等的等边三角形一定相似,不符合题意;
D、两个边长不等的正方形一定相似,不符合题意,
故选:B.
7.解:根据题意两个三角形的相似比是15:23,周长比就是15:23,
大小周长相差8份,所以每份的周长是40÷8=5cm,
所以两个三角形的周长分别为5×15=75cm,5×23=115cm.
故选:C.
8.解:过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H,
∵AB=AC,AD=AG,
∴AD:AB=AG:AC,
∵∠BAC=∠DAG,
∴△ADG∽△ABC,
∴∠ADG=∠B,
∴DG∥BC,
∵四边形DEFG是正方形,
∴FG⊥DG,
∴FH⊥BC,AN⊥DG,
∵AB=AC=10,BC=12,
∴BM=BC=6,
∴AM===8,
∵DG∥BC,
∴△ADG∽△ABC,
∴,
∴,
∴AN=2,
∴MN=AM﹣AN=6,
∴FH=MN﹣GF=6﹣3=3,
故选:A.
9.解:∵以原点O为位似中心,相似比为2,将△OAB放大为△OA′B′,点B(﹣1,2),
∴B′点的坐标为(﹣2,4)或(2,﹣4).
故选:D.
10.解:∵AB=AC,
∴∠B=∠C,
∵DA=DC,
∴∠DAC=∠C,
∴∠DAC=∠B,
∵∠C=∠C,
∴△CDA∽△CAB,
∴=,
∴CA2=CD?CB,
∵CA=a,BD=a,CD=1,
∴CB=1+a,
∴a2=1?(1+a),
∴a2﹣a﹣1=0,
∴a=或(舍弃),
故选:A.
二.填空题
11.解:过点D作DH⊥OE于点H,
由题意可得:BC=3,OE=6,△ABC∽△DOE,
则位似比为:3:6=1:2,
故OH=2OB=4,DH=2OA=6,
则D点的坐标为:(4,6),
由MO:MH=1:2,
MH=MO+4,
故MO:(MO+4)=1:2,
解得:MO=4,
则M点坐标为:(﹣4,0).
故答案为:(﹣4,0).
12.解:∵∠C=90°,CD⊥AB,
∴AC2=AD?AB,
∴AC是AD和AB的比例中项,
故答案为:AB.
13.解:∵四边形ABCD∽四边形A'B'C'D',
∴CD:C′D′=BC:B′C′,
∵BC=3,CD=2.4,B'C′=2,
∴C′D′=1.6,
故答案为:1.6.
14.解:∵两个相似三角形的相似比为3:2,
∴它们对应周长的比为3:2;
对应面积的比是(3:2)2=9:4.
故答案为:3:2;9:4.
15.解:∵线段b是a、c的比例中项,
∴b2=ac=16,
解得:b=±4,
又∵线段是正数,
∴b=4(厘米).
故答案为:4.
16.解:∵=,
∴=+1=+1=.
故答案为:.
17.解:如图,AM、BN都与水平线的垂直,M,N是垂足,则AM∥BN,
∵AM∥BN,
∴△ACM∽△BCN,
∴=,
∵AC与BC之比为6:1,
∴==6,即AM=6BN,
∴当BN≥10cm时,AM≥60cm,
故要使这块石头滚动,至少要将杠杆的A端向下压60cm.
故答案为:60.
18.解:①∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,
∵PM⊥AC,
∴∠AEP=∠AEM=90°,
在△APE和△AME中,
,
∴△APE≌△AME(ASA),
故①正确;
②∵△APE≌△AME,
∴PE=EM=PM,
同理,FP=FN=NP,
∵正方形ABCD中,AC⊥BD,
又∵PE⊥AC,PF⊥BD,
∴∠PEO=∠EOF=∠PFO=90°,且△APE中AE=PE
∴四边形PEOF是矩形.
∴PF=OE,
在△APE中,∠AEP=90°,∠PAE=45°,
∴△APE为等腰直角三角形,
∴AE=PE,
∴PE+PF=OA,
又∵PE=EM=PM,FP=FN=NP,OA=AC,
∴PM+PN=AC,
故②正确;
③∵四边形PEOF是矩形,
∴PE=OF,
在直角△OPF中,OF2+PF2=PO2,
∴PE2+PF2=PO2,
故③正确;
④∵△APE≌△AME,
∴AP=AM
△BNF是等腰直角三角形,而△POF不一定是,
∴△POF与△BNF不一定相似,
故④错误;
⑤∵△APE≌△AME,
∴ME=PE,
∴AE是MP是中垂线,
∴MO=OP,
又∵OE⊥MP,
∴∠MOE=∠POE,
同理可证∠POF=∠NOF,
∵∠POE+∠POF=∠EOF=90°,
∴∠MOE+∠POE+∠POF+∠NOF=180°,
∴点M,点O,点N三点共线,
故⑤正确,
故答案为①②③⑤.
19.解:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB或=时,△ACP∽△ABC,
故答案为:∠ACP=∠B,或∠APC=∠ACB或=.
20.解:∵点E是边BC上的黄金分割点,且BE>CE,
∴BE=BC,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BE,
∴△EBF∽△ADF,
∴==,
∴=,
故答案为.
三.解答题
21.解:设a=3k,b=2k,c=k,
∵2a﹣3b+c=10,
∴6k﹣6k+k=10,
∴k=10,
∴a=30,b=20,c=10,
∴a+2b﹣3c=30+40﹣30=40.
22.解:(1)如图,△A1B1C1为所作;
(2)如图,△A2BC2为所作;
(3)△CC1C2的面积=×3×6=9;
A1的坐标为(7,9);A2的坐标为(3,5).
23.解:∵四边形AEFD是正方形,
∴AE=AD=2,
∵矩形ABCD为黄金矩形,
∴AD=AB,
即2=AB,
解得:AB=+1,
∴BE=AB﹣AE=+1﹣2=﹣1.
24.解:∵DE∥BC,
∴,
又∵AE:EC=3:2,
∴,
∴,
又∵AB=15,
∴,
解得:BD=6.
25.解:存在,如图,点F即为所求.
理由:∵OA=OC,OF⊥AC,
∴FA=FC,
∴∠AFO=∠CFO,
∵∠BAD=∠AOF=90°,
∴∠EAO+∠FAO=90°,∠FAO+∠AFO=90°,
∴∠EAO=∠AFO=∠CFO,
∵AE=EB,AO=OC,
∴OE∥BC,
∴∠AEO=∠B=90°,
∴∠AEO=∠FOC=90°,
∴△CFO∽△CAE.
26.解:(1)如图,△DEF即为所求.
(2)S△ABC=×3×1=,S△DEF=×6×2=6,AB=,DE=2,
∴=()2,
27.证明:(1)∵AQ∥PC,
∴∠AQE=∠CPD,
由题意知,AE∥CD,,
∴∠AEQ=∠CDP,
∴ΔAEQ∽ΔCDP,
∴,
∴PC=2AQ;
(2)∵AD2=PD?DE,
即,
∵∠ADP=∠EDA,
∴ΔADP∽ΔEDA,
∴∠DAP=∠DEA,
∵AD∥BC,
∴∠DAP=∠AFB,
∴∠DEA=∠AFB,
在矩形ABCD中,∠DAE=∠ABF=90°,
∴ΔDAE∽ΔABF,
∴,即,
∴;
(3)如图,延长DE交CB的延长线于点G,
∵点E是AB的中点,
∴AE=BE,
∵AD∥BC,
∴∠ADE=∠BGE,
∵∠AED=∠BEG,
∴ΔADE≌ΔBGE(AAS),
∴AD=BG,
又AD=BC,
∴GC=BG+BC=2AD,
又点F为BC的中点,
∴BC=2BF,
∴AD=2BF,BG=2BF,
∴GF=BG+BF=3BF,
∴,
由题意知,AD∥GC,
∴ΔAPD∽ΔFPG,
∴.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
