2020-2021学年苏科新版九年级下册数学《第7章 锐角三角函数》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年苏科新版九年级下册数学《第7章 锐角三角函数》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 414.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 22:25:15 | ||
图片预览

文档简介
2020-2021学年苏科新版九年级下册数学《第7章
锐角三角函数》单元测试卷
一.选择题
1.如果∠A为锐角,sinA=,那么( )
A.0°<∠A<30°
B.30°<∠A<45°
C.45°<∠A<60°
D.60°<∠A<90°
2.在Rt△ABC中,∠C=90°,下列式子正确的是( )
A.sinA+cosA<1
B.sinA+cosA=1
C.sinA+cosA>1
D.sinA+cosA≥1
3.当锐角A的cosA>时,∠A的值为( )
A.小于45°
B.小于30°
C.大于45°
D.大于30°
4.计算2cos30°的结果等于( )
A.
B.
C.
D.
5.已知sinα=,求α.若以科学计算器计算且结果以“度,分,秒”为单位,最后应该按键( )
A.AC
B.2ndF
C.MODE
D.DMS
6.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°
B.10cos36°
C.10sin36°
D.
7.在Rt△ABC中,锐角A的对边和斜边同时扩大100倍,sinA的值( )
A.扩大100倍
B.缩小
C.不变
D.不能确定
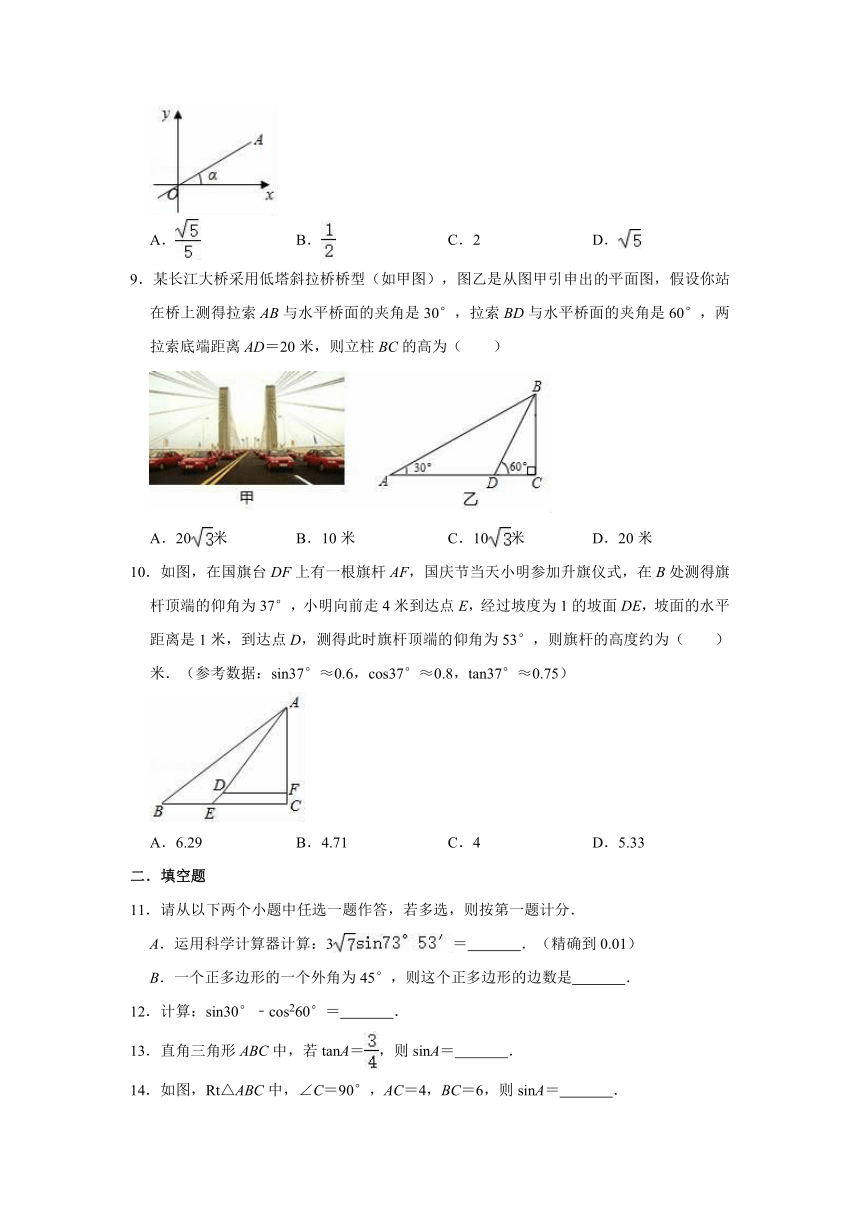
8.如图,直线OA过点(2,1),直线OA与x轴的夹角为α,则tanα的值为( )
A.
B.
C.2
D.
9.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米
B.10米
C.10米
D.20米
10.如图,在国旗台DF上有一根旗杆AF,国庆节当天小明参加升旗仪式,在B处测得旗杆顶端的仰角为37°,小明向前走4米到达点E,经过坡度为1的坡面DE,坡面的水平距离是1米,到达点D,测得此时旗杆顶端的仰角为53°,则旗杆的高度约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.6.29
B.4.71
C.4
D.5.33
二.填空题
11.请从以下两个小题中任选一题作答,若多选,则按第一题计分.
A.运用科学计算器计算:3=
.(精确到0.01)
B.一个正多边形的一个外角为45°,则这个正多边形的边数是
.
12.计算:sin30°﹣cos260°=
.
13.直角三角形ABC中,若tanA=,则sinA=
.
14.如图,Rt△ABC中,∠C=90°,AC=4,BC=6,则sinA=
.
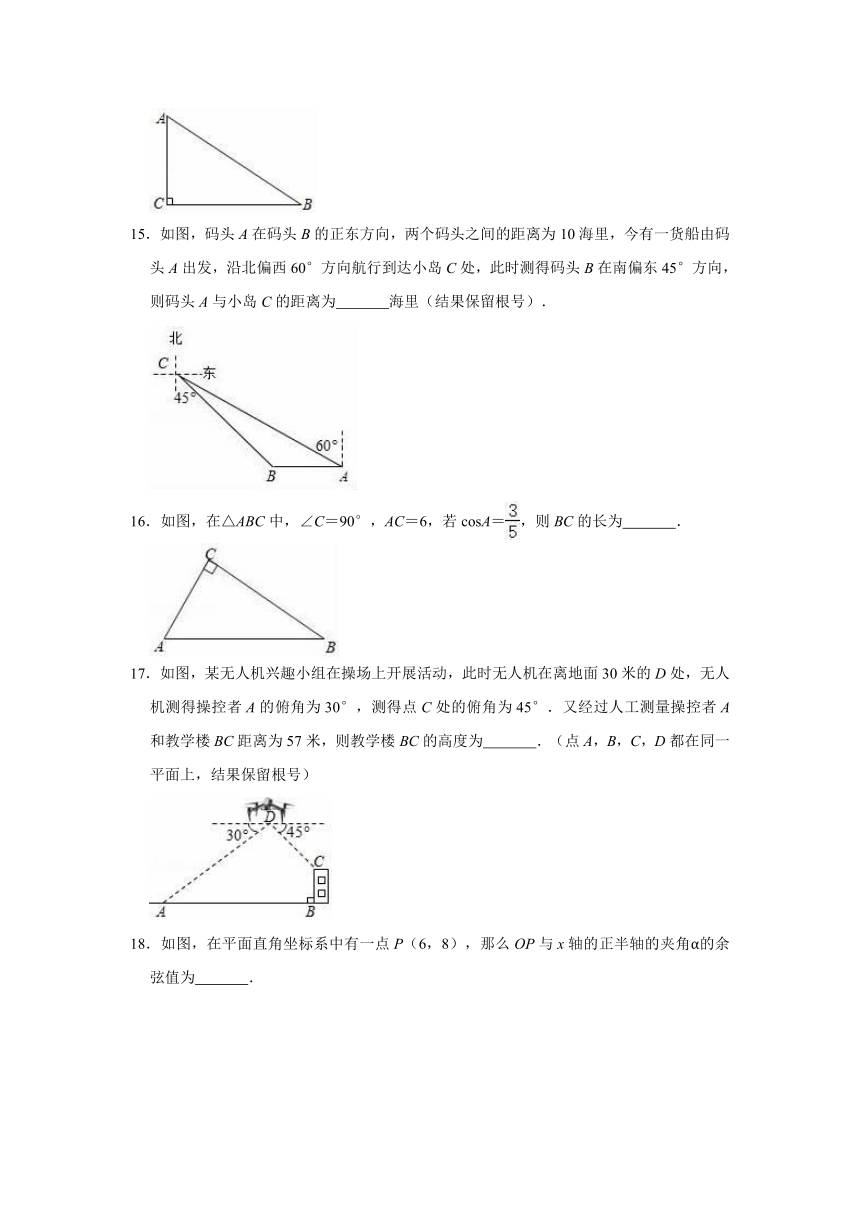
15.如图,码头A在码头B的正东方向,两个码头之间的距离为10海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,则码头A与小岛C的距离为
海里(结果保留根号).
16.如图,在△ABC中,∠C=90°,AC=6,若cosA=,则BC的长为
.
17.如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,则教学楼BC的高度为
.(点A,B,C,D都在同一平面上,结果保留根号)
18.如图,在平面直角坐标系中有一点P(6,8),那么OP与x轴的正半轴的夹角α的余弦值为
.
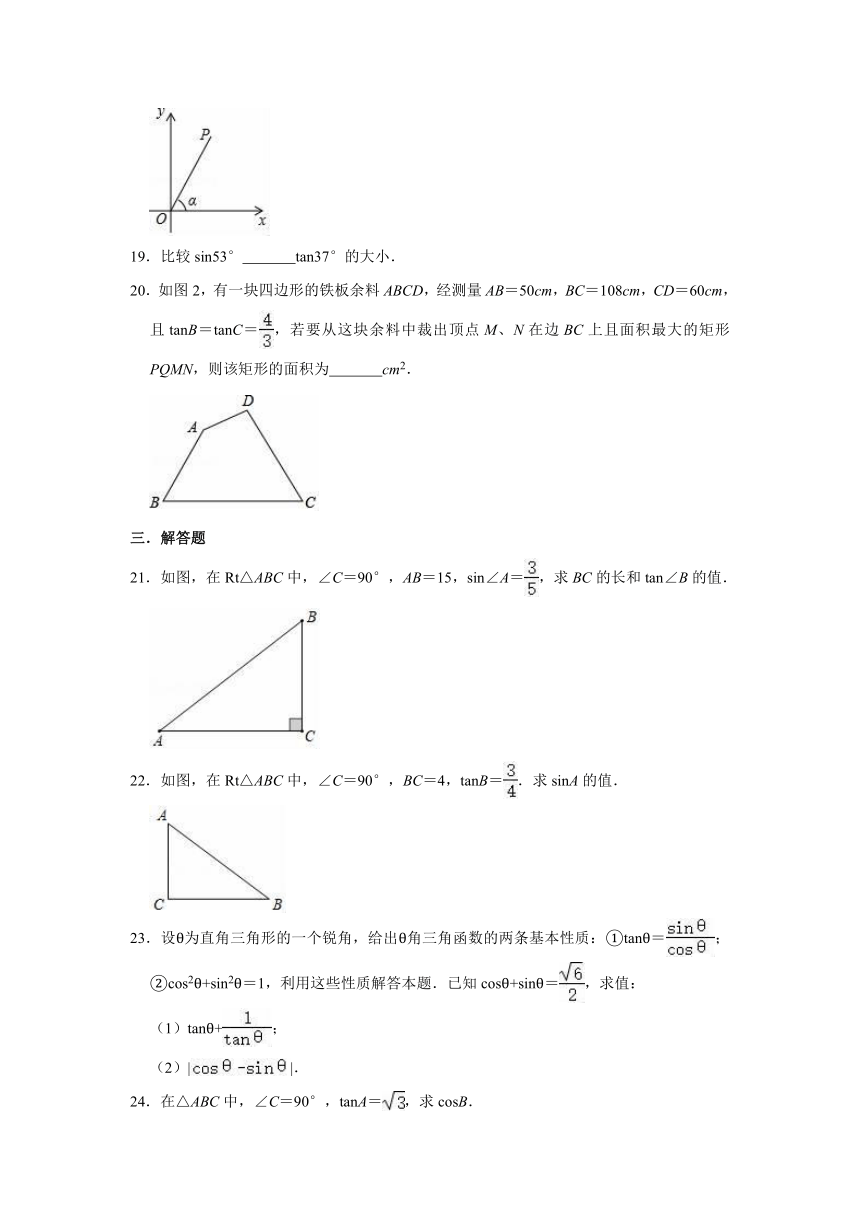
19.比较sin53°
tan37°的大小.
20.如图2,有一块四边形的铁板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=,若要从这块余料中裁出顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为
cm2.
三.解答题
21.如图,在Rt△ABC中,∠C=90°,AB=15,sin∠A=,求BC的长和tan∠B的值.
22.如图,在Rt△ABC中,∠C=90°,BC=4,tanB=.求sinA的值.
23.设θ为直角三角形的一个锐角,给出θ角三角函数的两条基本性质:①tanθ=;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=,求值:
(1)tanθ+;
(2)||.
24.在△ABC中,∠C=90°,tanA=,求cosB.
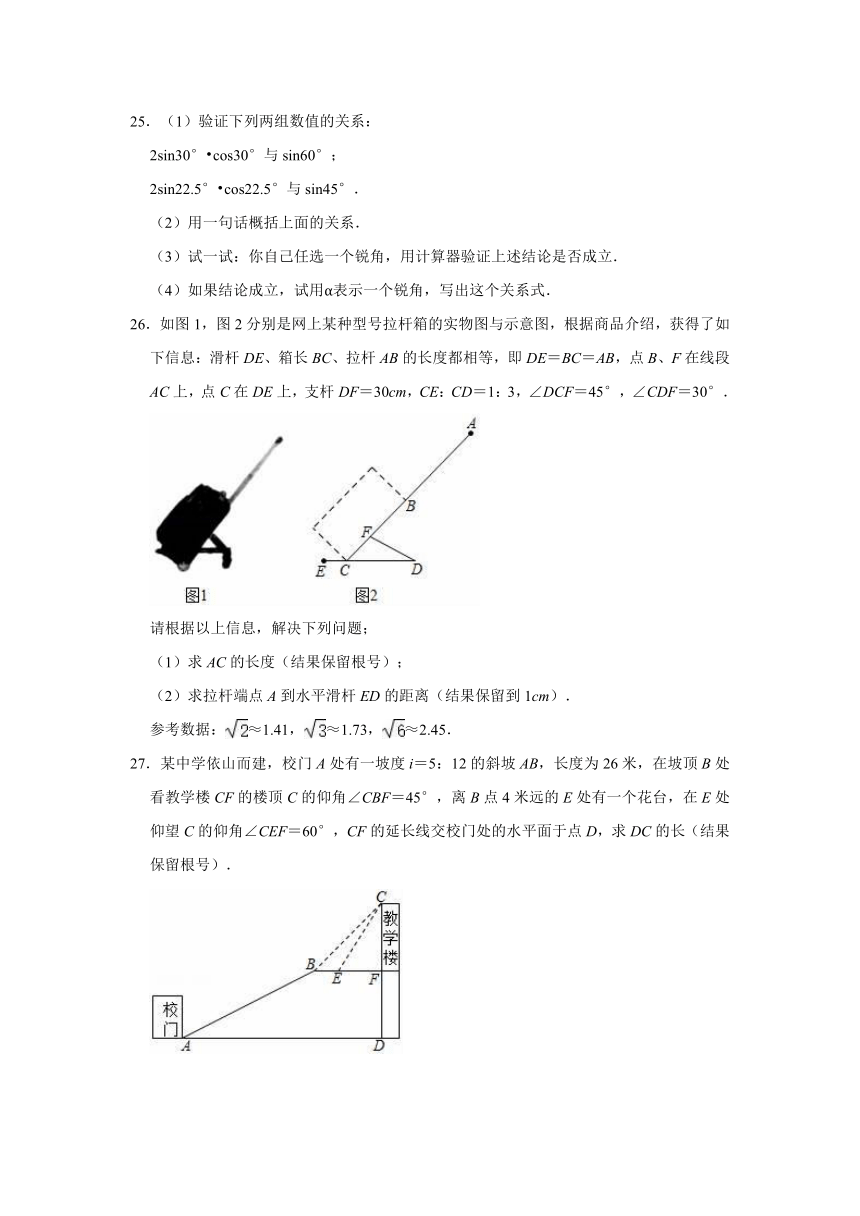
25.(1)验证下列两组数值的关系:
2sin30°?cos30°与sin60°;
2sin22.5°?cos22.5°与sin45°.
(2)用一句话概括上面的关系.
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
26.如图1,图2分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆DE、箱长BC、拉杆AB的长度都相等,即DE=BC=AB,点B、F在线段AC上,点C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°.
请根据以上信息,解决下列问题;
(1)求AC的长度(结果保留根号);
(2)求拉杆端点A到水平滑杆ED的距离(结果保留到1cm).
参考数据:≈1.41,≈1.73,≈2.45.
27.某中学依山而建,校门A处有一坡度i=5:12的斜坡AB,长度为26米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=45°,离B点4米远的E处有一个花台,在E处仰望C的仰角∠CEF=60°,CF的延长线交校门处的水平面于点D,求DC的长(结果保留根号).
参考答案与试题解析
一.选择题
1.解:∵sin30°=,0<<,
∴0°<∠A<30°.
故选:A.
2.解:∵sinA=,cosA=,
∴sinA+cosA=,
∵a+b>c,
∴sinA+cosA>1.
故选:C.
3.解:根据cos45°=,余弦函数随角增大而减小,则∠A一定小于45°.
故选:A.
4.解:2cos30°=2×=.
故选:D.
5.解:若以科学计算器计算且结果以“度,分,秒”为单位,最后应该按DMS,
故选:D.
6.解:在Rt△ABC中,sinB=,
∴AC=AB?sinB=10sin36°,
故选:C.
7.解:锐角A的三角函数值随着∠A角度的变化而变化,而角的大小与边的长短没有关系,
因此sinA的值不会随着边长的扩大而变化,
故选:C.
8.解:过点C(2,1)作CD⊥x轴于D,如图所示:
则OD=2,CD=1,
在Rt△OCD中,tanα==.
故选:B.
9.解:∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=60°,
∴∠ABD=60°﹣30°=30°,
∴∠A=∠ABD,
∴BD=AD=20米,
∴BC=BD?sin60°=10(米),
故选:C.
10.解:过点D作DM⊥BC,垂足为M,由题意得,
∠B=37°,∠ADF=53°,BE=4,EM=1,
∵坡面DE的坡度为1,
∴=1,
∴DM=EM=1=FC,
在Rt△ADF中,∠DAF=90°﹣∠ADF=90°﹣53°=37°,
∵tan∠DAF=≈0.75,
设AF=x,则DF=0.75x=MC,
在Rt△ABC中,
∵tan∠B=,
∴tan37°=≈0.75,
解得x=≈6.29(米),
故选:A.
二.填空题
11.解:(1)原式≈3×2.64×0.9607≈7.61;
(2)由于正多边形的一个外角为45°,
∴正多边形的边数为:=8;
故答案为:(1)7.61;(2)8;
12.解:sin30°﹣cos260°=﹣()2
=﹣
=.
故答案为:.
13.解:如图所示:
∵tanA==,
∴设BC=3x,则AC=4x,
∴AB=5x,
则sinA===.
故答案为:.
14.解:在Rt△ABC中,∵∠C=90°,AC=4,BC=6,
∴AB===2,
则sinA===,
故答案为:.
15.解:作CD⊥AB交AB延长线于点D,
由题意,得∠DCB=45°,∠CAD=90°﹣60°=30°,AB=10海里,
设CD=x海里,
在Rt△DCB中,tan∠DCB=,tan45°==1,
∴BD=x,
则AD=AB+BD=10+x,
由tan30°=,
解得x=5+5,
∵∠CAD=30°,∠CDA=90°,
∴AC=2CD=(10+10)海里.
故答案为:(10+10).
16.解:∵在△ABC中,∠C=90°,AC=6,cosA=,
∴cosA===,
∴AB=10,
∴BC====8.
故答案为:8.
17.解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F.
由题意得,AB=57,DE=30,∠A=30°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,
∴tan30°=,
即=,
∴AE=30,
∵AB=57,
∴BE=AB﹣AE=57﹣30,
∵四边形BCFE是矩形,
∴CF=BE=57﹣30.
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°.
∴DF=CF=57﹣30,
∴BC=EF=30﹣57+30=(30﹣27)米.
答:教学楼BC高约(30﹣27)米.
故答案为:(30﹣27)米.
18.解:如图作PH⊥x轴于H.
∵P(6,8),
∴OH=6,PH=8,
∴OP==10,
∴cosα===.
故答案为:.
19.解:如图,Rt△ABC中,∠C=90°,∠A=53°,∠B=37°.则AC=3,BC=4,AB=5,
∵sin53°===0.8,tan37°===0.75,
∴sin53°>tan37°.
故答案为>
20.解:如图,延长BA、CD交于点E,过点E作EH⊥BC于点H,
交PQ于点G,如图,设矩形PQMN,
∵tanB=tanC=,
∴∠B=∠C,
∴EB=EC,
∵BC=108cm,且EH⊥BC,
∴BH=CH=BC=54cm,
∵tanB==,
∴EH=BH=×54=72cm,
∴EG=EH﹣GH=72﹣QM,
∵PQ∥BC,
∴△AQP∽△ABC,
∴=,即=,
∴PQ=(72﹣QM),
设QM=x,
则S矩形PQMN=PQ?QM=x(72﹣x)=﹣(x﹣36)2+1944,
∴当x=36时,S矩形PQMN最大值为1944,
所以当QM=36时,矩形PQMN的最大面积为1944cm2,
答:该矩形的面积为1944cm2.
故答案为:1944.
三.解答题
21.解:∵sin∠A=,
∴=,
∵AB=15,
∴BC=9;
∴AC==12,
∴tan∠B===.
22.解:在Rt△ABC中,
∵∠C=90°,BC=4,
∴tanB==,
∴AC=3,
∵AB2=AC2+BC2,
∴AB=5,
∴sinA==.
23.解(1)∵cosθ+sinθ=,
∴(cosθ+sinθ)2=()2,
cos2θ+2cosθ?sinθ+sin2θ=,
cosθ?sinθ=,
∴tanθ+=+===4;
(2)∵(cosθ﹣sinθ)2=cos2θ﹣2cosθ?sinθ+sin2θ=1﹣2×=,
∴cosθ﹣sinθ=±,
∴|cosθ﹣sinθ|=.
24.解:∵tanA=,
∴∠A=60°.
∵∠A+∠B=90°,
∴∠B=90°﹣60°=30°.
∴cosB=.
25.解:(1)∵2sin30°?cos30°=2××=,sin60°=.
2sin22.5°?cos22.5≈2×0.38×0.92≈0.7,sin45°=≈0.7,
∴2sin30°?cos30°=sin60°,2sin22.5°?cos22.5=sin45°;
(2)由(1)可知,一个角正弦与余弦积的2倍,等于该角2倍的正弦值;
(3)2sin15°?cos15°≈2×0.26×0.97≈,sin30°=;
故结论成立;
(4)2sinα?cosα=sin2α.
26.解:(1)过F作FH⊥DE于H.∴∠FHC=∠FHD=90°.
∵∠FDC=30°,DF=30,
∴,,
∵∠FCH=45°,
∴CH=FH=15,
∴,
∵CE:CD=1:3,
∴,
∵AB=BC=DE,
∴;
(2)过A作AG⊥ED交ED的延长线于G,
∵∠ACG=45°,
∴=20×1.41+20×2.45=77.2≈77(cm)
答:拉杆端点A到水平滑杆ED的距离为77cm.
27.解:过点B作BM⊥AD于M,如图所示:
∵i=5:12,
∴=,
∵AB=26米,
∴BM=10米,AM=24米,
∴DF=BM=10米,
设EF为x米,则BF=(4+x)米,
∵∠CBF=45°,
∴BF=CF=(4+x)米,
∵∠CEF=60°,
∴tan60°=,
即=,
解得:x=2+2,
∴CF=(6+2)米,
∴CD=CF+DF=6+2+10=16+2(米),
答:DC的长度为(16+2)米.
锐角三角函数》单元测试卷
一.选择题
1.如果∠A为锐角,sinA=,那么( )
A.0°<∠A<30°
B.30°<∠A<45°
C.45°<∠A<60°
D.60°<∠A<90°
2.在Rt△ABC中,∠C=90°,下列式子正确的是( )
A.sinA+cosA<1
B.sinA+cosA=1
C.sinA+cosA>1
D.sinA+cosA≥1
3.当锐角A的cosA>时,∠A的值为( )
A.小于45°
B.小于30°
C.大于45°
D.大于30°
4.计算2cos30°的结果等于( )
A.
B.
C.
D.
5.已知sinα=,求α.若以科学计算器计算且结果以“度,分,秒”为单位,最后应该按键( )
A.AC
B.2ndF
C.MODE
D.DMS
6.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°
B.10cos36°
C.10sin36°
D.
7.在Rt△ABC中,锐角A的对边和斜边同时扩大100倍,sinA的值( )
A.扩大100倍
B.缩小
C.不变
D.不能确定
8.如图,直线OA过点(2,1),直线OA与x轴的夹角为α,则tanα的值为( )
A.
B.
C.2
D.
9.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米
B.10米
C.10米
D.20米
10.如图,在国旗台DF上有一根旗杆AF,国庆节当天小明参加升旗仪式,在B处测得旗杆顶端的仰角为37°,小明向前走4米到达点E,经过坡度为1的坡面DE,坡面的水平距离是1米,到达点D,测得此时旗杆顶端的仰角为53°,则旗杆的高度约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.6.29
B.4.71
C.4
D.5.33
二.填空题
11.请从以下两个小题中任选一题作答,若多选,则按第一题计分.
A.运用科学计算器计算:3=
.(精确到0.01)
B.一个正多边形的一个外角为45°,则这个正多边形的边数是
.
12.计算:sin30°﹣cos260°=
.
13.直角三角形ABC中,若tanA=,则sinA=
.
14.如图,Rt△ABC中,∠C=90°,AC=4,BC=6,则sinA=
.
15.如图,码头A在码头B的正东方向,两个码头之间的距离为10海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,则码头A与小岛C的距离为
海里(结果保留根号).
16.如图,在△ABC中,∠C=90°,AC=6,若cosA=,则BC的长为
.
17.如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,则教学楼BC的高度为
.(点A,B,C,D都在同一平面上,结果保留根号)
18.如图,在平面直角坐标系中有一点P(6,8),那么OP与x轴的正半轴的夹角α的余弦值为
.
19.比较sin53°
tan37°的大小.
20.如图2,有一块四边形的铁板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=,若要从这块余料中裁出顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为
cm2.
三.解答题
21.如图,在Rt△ABC中,∠C=90°,AB=15,sin∠A=,求BC的长和tan∠B的值.
22.如图,在Rt△ABC中,∠C=90°,BC=4,tanB=.求sinA的值.
23.设θ为直角三角形的一个锐角,给出θ角三角函数的两条基本性质:①tanθ=;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=,求值:
(1)tanθ+;
(2)||.
24.在△ABC中,∠C=90°,tanA=,求cosB.
25.(1)验证下列两组数值的关系:
2sin30°?cos30°与sin60°;
2sin22.5°?cos22.5°与sin45°.
(2)用一句话概括上面的关系.
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
26.如图1,图2分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆DE、箱长BC、拉杆AB的长度都相等,即DE=BC=AB,点B、F在线段AC上,点C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°.
请根据以上信息,解决下列问题;
(1)求AC的长度(结果保留根号);
(2)求拉杆端点A到水平滑杆ED的距离(结果保留到1cm).
参考数据:≈1.41,≈1.73,≈2.45.
27.某中学依山而建,校门A处有一坡度i=5:12的斜坡AB,长度为26米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=45°,离B点4米远的E处有一个花台,在E处仰望C的仰角∠CEF=60°,CF的延长线交校门处的水平面于点D,求DC的长(结果保留根号).
参考答案与试题解析
一.选择题
1.解:∵sin30°=,0<<,
∴0°<∠A<30°.
故选:A.
2.解:∵sinA=,cosA=,
∴sinA+cosA=,
∵a+b>c,
∴sinA+cosA>1.
故选:C.
3.解:根据cos45°=,余弦函数随角增大而减小,则∠A一定小于45°.
故选:A.
4.解:2cos30°=2×=.
故选:D.
5.解:若以科学计算器计算且结果以“度,分,秒”为单位,最后应该按DMS,
故选:D.
6.解:在Rt△ABC中,sinB=,
∴AC=AB?sinB=10sin36°,
故选:C.
7.解:锐角A的三角函数值随着∠A角度的变化而变化,而角的大小与边的长短没有关系,
因此sinA的值不会随着边长的扩大而变化,
故选:C.
8.解:过点C(2,1)作CD⊥x轴于D,如图所示:
则OD=2,CD=1,
在Rt△OCD中,tanα==.
故选:B.
9.解:∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=60°,
∴∠ABD=60°﹣30°=30°,
∴∠A=∠ABD,
∴BD=AD=20米,
∴BC=BD?sin60°=10(米),
故选:C.
10.解:过点D作DM⊥BC,垂足为M,由题意得,
∠B=37°,∠ADF=53°,BE=4,EM=1,
∵坡面DE的坡度为1,
∴=1,
∴DM=EM=1=FC,
在Rt△ADF中,∠DAF=90°﹣∠ADF=90°﹣53°=37°,
∵tan∠DAF=≈0.75,
设AF=x,则DF=0.75x=MC,
在Rt△ABC中,
∵tan∠B=,
∴tan37°=≈0.75,
解得x=≈6.29(米),
故选:A.
二.填空题
11.解:(1)原式≈3×2.64×0.9607≈7.61;
(2)由于正多边形的一个外角为45°,
∴正多边形的边数为:=8;
故答案为:(1)7.61;(2)8;
12.解:sin30°﹣cos260°=﹣()2
=﹣
=.
故答案为:.
13.解:如图所示:
∵tanA==,
∴设BC=3x,则AC=4x,
∴AB=5x,
则sinA===.
故答案为:.
14.解:在Rt△ABC中,∵∠C=90°,AC=4,BC=6,
∴AB===2,
则sinA===,
故答案为:.
15.解:作CD⊥AB交AB延长线于点D,
由题意,得∠DCB=45°,∠CAD=90°﹣60°=30°,AB=10海里,
设CD=x海里,
在Rt△DCB中,tan∠DCB=,tan45°==1,
∴BD=x,
则AD=AB+BD=10+x,
由tan30°=,
解得x=5+5,
∵∠CAD=30°,∠CDA=90°,
∴AC=2CD=(10+10)海里.
故答案为:(10+10).
16.解:∵在△ABC中,∠C=90°,AC=6,cosA=,
∴cosA===,
∴AB=10,
∴BC====8.
故答案为:8.
17.解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F.
由题意得,AB=57,DE=30,∠A=30°,∠DCF=45°.
在Rt△ADE中,∠AED=90°,
∴tan30°=,
即=,
∴AE=30,
∵AB=57,
∴BE=AB﹣AE=57﹣30,
∵四边形BCFE是矩形,
∴CF=BE=57﹣30.
在Rt△DCF中,∠DFC=90°,
∴∠CDF=∠DCF=45°.
∴DF=CF=57﹣30,
∴BC=EF=30﹣57+30=(30﹣27)米.
答:教学楼BC高约(30﹣27)米.
故答案为:(30﹣27)米.
18.解:如图作PH⊥x轴于H.
∵P(6,8),
∴OH=6,PH=8,
∴OP==10,
∴cosα===.
故答案为:.
19.解:如图,Rt△ABC中,∠C=90°,∠A=53°,∠B=37°.则AC=3,BC=4,AB=5,
∵sin53°===0.8,tan37°===0.75,
∴sin53°>tan37°.
故答案为>
20.解:如图,延长BA、CD交于点E,过点E作EH⊥BC于点H,
交PQ于点G,如图,设矩形PQMN,
∵tanB=tanC=,
∴∠B=∠C,
∴EB=EC,
∵BC=108cm,且EH⊥BC,
∴BH=CH=BC=54cm,
∵tanB==,
∴EH=BH=×54=72cm,
∴EG=EH﹣GH=72﹣QM,
∵PQ∥BC,
∴△AQP∽△ABC,
∴=,即=,
∴PQ=(72﹣QM),
设QM=x,
则S矩形PQMN=PQ?QM=x(72﹣x)=﹣(x﹣36)2+1944,
∴当x=36时,S矩形PQMN最大值为1944,
所以当QM=36时,矩形PQMN的最大面积为1944cm2,
答:该矩形的面积为1944cm2.
故答案为:1944.
三.解答题
21.解:∵sin∠A=,
∴=,
∵AB=15,
∴BC=9;
∴AC==12,
∴tan∠B===.
22.解:在Rt△ABC中,
∵∠C=90°,BC=4,
∴tanB==,
∴AC=3,
∵AB2=AC2+BC2,
∴AB=5,
∴sinA==.
23.解(1)∵cosθ+sinθ=,
∴(cosθ+sinθ)2=()2,
cos2θ+2cosθ?sinθ+sin2θ=,
cosθ?sinθ=,
∴tanθ+=+===4;
(2)∵(cosθ﹣sinθ)2=cos2θ﹣2cosθ?sinθ+sin2θ=1﹣2×=,
∴cosθ﹣sinθ=±,
∴|cosθ﹣sinθ|=.
24.解:∵tanA=,
∴∠A=60°.
∵∠A+∠B=90°,
∴∠B=90°﹣60°=30°.
∴cosB=.
25.解:(1)∵2sin30°?cos30°=2××=,sin60°=.
2sin22.5°?cos22.5≈2×0.38×0.92≈0.7,sin45°=≈0.7,
∴2sin30°?cos30°=sin60°,2sin22.5°?cos22.5=sin45°;
(2)由(1)可知,一个角正弦与余弦积的2倍,等于该角2倍的正弦值;
(3)2sin15°?cos15°≈2×0.26×0.97≈,sin30°=;
故结论成立;
(4)2sinα?cosα=sin2α.
26.解:(1)过F作FH⊥DE于H.∴∠FHC=∠FHD=90°.
∵∠FDC=30°,DF=30,
∴,,
∵∠FCH=45°,
∴CH=FH=15,
∴,
∵CE:CD=1:3,
∴,
∵AB=BC=DE,
∴;
(2)过A作AG⊥ED交ED的延长线于G,
∵∠ACG=45°,
∴=20×1.41+20×2.45=77.2≈77(cm)
答:拉杆端点A到水平滑杆ED的距离为77cm.
27.解:过点B作BM⊥AD于M,如图所示:
∵i=5:12,
∴=,
∵AB=26米,
∴BM=10米,AM=24米,
∴DF=BM=10米,
设EF为x米,则BF=(4+x)米,
∵∠CBF=45°,
∴BF=CF=(4+x)米,
∵∠CEF=60°,
∴tan60°=,
即=,
解得:x=2+2,
∴CF=(6+2)米,
∴CD=CF+DF=6+2+10=16+2(米),
答:DC的长度为(16+2)米.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
