苏科版七年级数学下册教案 7.1 探索直线平行的条件(表格式)
文档属性
| 名称 | 苏科版七年级数学下册教案 7.1 探索直线平行的条件(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 92.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览

文档简介
探索直线平行的条件(1)
教学目标
1.引导学生探索、理解、掌握直线平行的条件——同位角相等,并能在数学图形及实际生活中正确识别平行线;
2.经历探索两直线平行的条件的活动过程,提高对图形的认识、分析能力;体会说理的必要性,会进行简单的说理——根据图形中的已知条件,通过简单说理或推理,得出欲求结果.
教学重点
理解平行线的识别方法——同位角相等,两直线平行.
教学难点
会进行简单的说理.
教学过程(教师)
学生活动
设计思路
新课引入——情景导入:
欣赏图片,发现生活中的平行线,回顾平行线的定义和表示方法。
回答相关问题。
通过图片,让学生发现生活中的平行线,激发学生的求知欲。
探索活动:
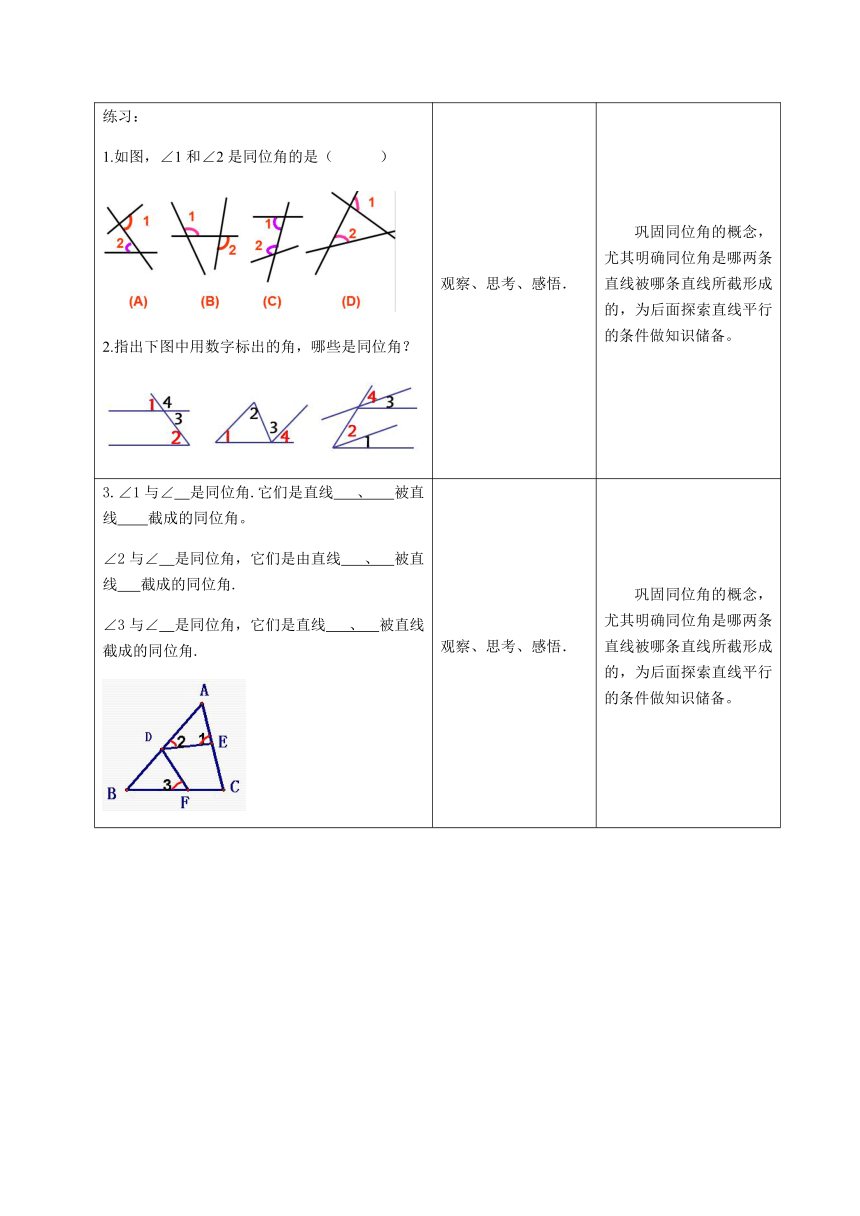
介绍“三线八角”中被截直线,截线的定义,从而得出同位角的定义,并让学生找出其他的同位角,并把它们从图形中分离出来,画出草图,发现同位角的结构特征。
熟悉同位角的定义,找出图中所有的同位角,探索发现所有的同位角都是F型的。
在判别“同位角”时,要注意“两同”:
1、在被截直线的同侧(左右);
2、在截线的同旁(上下)
练习:
1.如图,∠1和∠2是同位角的是( )
2.指出下图中用数字标出的角,哪些是同位角?
观察、思考、感悟.
巩固同位角的概念,尤其明确同位角是哪两条直线被哪条直线所截形成的,为后面探索直线平行的条件做知识储备。
3.∠1与∠
是同位角.它们是直线
、
被直线
截成的同位角。
∠2与∠
是同位角,它们是由直线
、
被直线
截成的同位角.
∠3与∠
是同位角,它们是直线
、
被直线
截成的同位角.
观察、思考、感悟.
巩固同位角的概念,尤其明确同位角是哪两条直线被哪条直线所截形成的,为后面探索直线平行的条件做知识储备。
探索活动:
1.如图,三根木条相交成∠1,
∠2,固定木条b、c,转动木条a
。观察随着∠2度数的变化,直线a和直线b的位置关系。
2.回忆如何画平行线。
通过以上两个活动,让学生总结归纳如何判断两条直线互相平行。
得出基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。简称为:同位角相等,两直线平行。
观察、思考,并归纳、小结得出“同位角相等,两直线平行”.并在图形变式中,体会“同位角不相等,两直线不平行”.
两个操作在这里发挥了很好的作用,给学生最直观的感受。知识不再是教师灌输,而是由学生体验感悟而得.课堂上,教师对课件做一简单操作后,∠2的度数发生了变化,∠1与∠2不相等了,随之,AB与CD不再平行了!学生很自然地得出了“同位角相等”、“两直线平行”之间的因果关系.
例题:
如图,∠1=∠C,∠1=∠2,请找出图中互相平行的直线,并说明理由.
(
1
)
如图,竖在地面上的两根旗杆,它们平行吗?请说明道理。
例2、如图,直线a、b被直线c所截,∠1=35°,
∠2=145°问:直线a与b平行吗?
(
c
)
开放题:
如图,直线a、b被直线c所截,∠1=
40°,能添加一个条件使得直线a与直线b平行吗?
发表意见,表达观点,相互补充.
参考答案:
因为∠1与∠C是AB、CD被AC所截构成的同位角,且∠1=∠C,所以AB∥CD.
由“∠1=∠C,∠1=∠2”可得∠2=∠C,而∠2与∠C是AC、BD被CD所截构成的同位角,所以AC∥BD.
因为b⊥c,
所以∠1=90°
同理∠2=90°
所以
∠1=∠2,
且∠1与∠2是a、b被c截成的同位角.
所以a∥b.
因为∠2=145°,
∠2+∠3=180°,
所以有∠3=35°,
而∠1=35°,
则∠1=∠3,
所以a//b。
让学生尽可能多的发觉条件。
师生互动,锻炼学生的口头表达能力,培养学生勇于发表自己看法的能力,会进行简单的说理.
在图形中准确地找到必需同位角是解题的前提。
开放性的问题设计,多样性的答案,既综合整理、当堂复习了新课知识要点,又留给了学生自由发挥的空间,也为下节课的探索做了铺垫。
小结:
通过今天的学习,你学会了什么?你会正确运用吗?通过这节课的学习,你有什么感受呢,说出来告诉大家.
共同小结.
师生互动,总结学习成果,体验成功.
课后作业:
1.课本P11习题7.1第2、3、4题;
2.思考题(选做):
已知:如图9,∠1=∠2,∠3=∠4.
(
(图9)
)问:(1)AB与CD平行吗?(2)EG与FH平行吗?为什么?
课后完成必做题,并根据自己的能力水平确定是否选做思考题.
选做题解法较多,但又不规定必须用几种方法,学生可根据自己的能力去自主选做.这样就能实现《课程标准》中所要求的“让不同层次的学生得到不同的发展”.
选做题中给出了“∠1=∠2”,即是为了考查学生简单的推理能力(推理得出一对同位角相等),也为下节课的引入埋下了伏笔.
教学目标
1.引导学生探索、理解、掌握直线平行的条件——同位角相等,并能在数学图形及实际生活中正确识别平行线;
2.经历探索两直线平行的条件的活动过程,提高对图形的认识、分析能力;体会说理的必要性,会进行简单的说理——根据图形中的已知条件,通过简单说理或推理,得出欲求结果.
教学重点
理解平行线的识别方法——同位角相等,两直线平行.
教学难点
会进行简单的说理.
教学过程(教师)
学生活动
设计思路
新课引入——情景导入:
欣赏图片,发现生活中的平行线,回顾平行线的定义和表示方法。
回答相关问题。
通过图片,让学生发现生活中的平行线,激发学生的求知欲。
探索活动:
介绍“三线八角”中被截直线,截线的定义,从而得出同位角的定义,并让学生找出其他的同位角,并把它们从图形中分离出来,画出草图,发现同位角的结构特征。
熟悉同位角的定义,找出图中所有的同位角,探索发现所有的同位角都是F型的。
在判别“同位角”时,要注意“两同”:
1、在被截直线的同侧(左右);
2、在截线的同旁(上下)
练习:
1.如图,∠1和∠2是同位角的是( )
2.指出下图中用数字标出的角,哪些是同位角?
观察、思考、感悟.
巩固同位角的概念,尤其明确同位角是哪两条直线被哪条直线所截形成的,为后面探索直线平行的条件做知识储备。
3.∠1与∠
是同位角.它们是直线
、
被直线
截成的同位角。
∠2与∠
是同位角,它们是由直线
、
被直线
截成的同位角.
∠3与∠
是同位角,它们是直线
、
被直线
截成的同位角.
观察、思考、感悟.
巩固同位角的概念,尤其明确同位角是哪两条直线被哪条直线所截形成的,为后面探索直线平行的条件做知识储备。
探索活动:
1.如图,三根木条相交成∠1,
∠2,固定木条b、c,转动木条a
。观察随着∠2度数的变化,直线a和直线b的位置关系。
2.回忆如何画平行线。
通过以上两个活动,让学生总结归纳如何判断两条直线互相平行。
得出基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。简称为:同位角相等,两直线平行。
观察、思考,并归纳、小结得出“同位角相等,两直线平行”.并在图形变式中,体会“同位角不相等,两直线不平行”.
两个操作在这里发挥了很好的作用,给学生最直观的感受。知识不再是教师灌输,而是由学生体验感悟而得.课堂上,教师对课件做一简单操作后,∠2的度数发生了变化,∠1与∠2不相等了,随之,AB与CD不再平行了!学生很自然地得出了“同位角相等”、“两直线平行”之间的因果关系.
例题:
如图,∠1=∠C,∠1=∠2,请找出图中互相平行的直线,并说明理由.
(
1
)
如图,竖在地面上的两根旗杆,它们平行吗?请说明道理。
例2、如图,直线a、b被直线c所截,∠1=35°,
∠2=145°问:直线a与b平行吗?
(
c
)
开放题:
如图,直线a、b被直线c所截,∠1=
40°,能添加一个条件使得直线a与直线b平行吗?
发表意见,表达观点,相互补充.
参考答案:
因为∠1与∠C是AB、CD被AC所截构成的同位角,且∠1=∠C,所以AB∥CD.
由“∠1=∠C,∠1=∠2”可得∠2=∠C,而∠2与∠C是AC、BD被CD所截构成的同位角,所以AC∥BD.
因为b⊥c,
所以∠1=90°
同理∠2=90°
所以
∠1=∠2,
且∠1与∠2是a、b被c截成的同位角.
所以a∥b.
因为∠2=145°,
∠2+∠3=180°,
所以有∠3=35°,
而∠1=35°,
则∠1=∠3,
所以a//b。
让学生尽可能多的发觉条件。
师生互动,锻炼学生的口头表达能力,培养学生勇于发表自己看法的能力,会进行简单的说理.
在图形中准确地找到必需同位角是解题的前提。
开放性的问题设计,多样性的答案,既综合整理、当堂复习了新课知识要点,又留给了学生自由发挥的空间,也为下节课的探索做了铺垫。
小结:
通过今天的学习,你学会了什么?你会正确运用吗?通过这节课的学习,你有什么感受呢,说出来告诉大家.
共同小结.
师生互动,总结学习成果,体验成功.
课后作业:
1.课本P11习题7.1第2、3、4题;
2.思考题(选做):
已知:如图9,∠1=∠2,∠3=∠4.
(
(图9)
)问:(1)AB与CD平行吗?(2)EG与FH平行吗?为什么?
课后完成必做题,并根据自己的能力水平确定是否选做思考题.
选做题解法较多,但又不规定必须用几种方法,学生可根据自己的能力去自主选做.这样就能实现《课程标准》中所要求的“让不同层次的学生得到不同的发展”.
选做题中给出了“∠1=∠2”,即是为了考查学生简单的推理能力(推理得出一对同位角相等),也为下节课的引入埋下了伏笔.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
