北师大版八年级数学上册第三章3.1---3.3知识过关检测题(word版 含解析)
文档属性
| 名称 | 北师大版八年级数学上册第三章3.1---3.3知识过关检测题(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 466.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 16:35:41 | ||
图片预览

文档简介
北师大版八年级数学上册第三章3.1---3.3知识过关检测题含答案
3.1确定位置
一、选择题
1.根据下列表述,能确定位置的是( )
A.红星电影院2排
B.北京市四环路
C.北偏东30°
D.东经118°,北纬40°
2.海事救灾船前去救援某海域失火的轮船,需要确定(
).
A.方位角
B.距离
C.失火轮船的船长
D.方位角和距离
3.电影院的第3排第6座表示为(3,6).若某同学的座位号为(4,2),那么该同学的位置是( )
A.第2排第4座
B.第4排第2座
C.第4座第4排
D.无法确定
4.如图是丁丁画的一张脸的示意图,如果用(0,2)表示靠左边的眼睛,用(2,2)表示靠右边的眼睛,那么嘴的位置可以表示成( )
A.(1,0)
B.(﹣1,0)
C.(﹣1,1)
D.(1,﹣1)
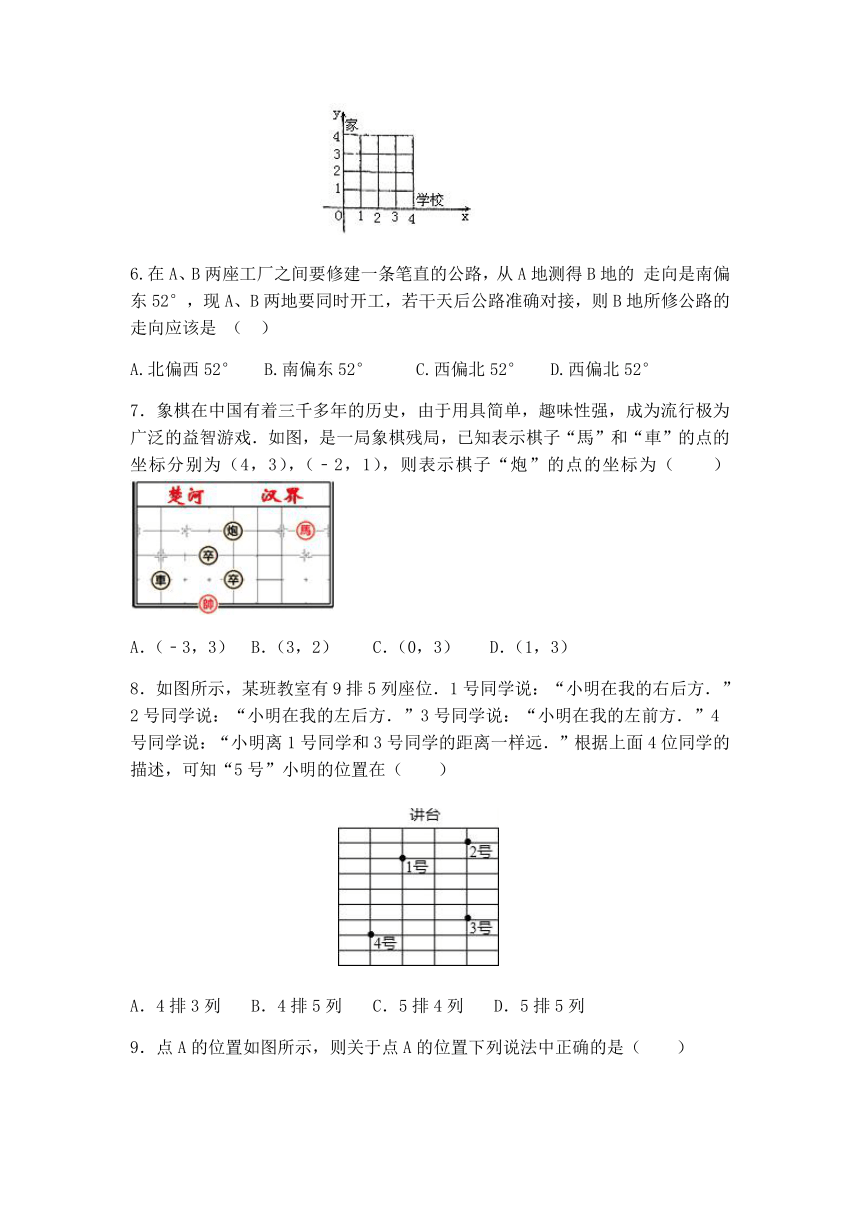
5.如图所示,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,小明走下面哪条线路不能到达学校(
).
A.(0,4)→(0,0)→(4,0)
B.(0,4)→(4,4)→(4,0)
C.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)
D.(0,4)→(3,4)→(4,2)→(4,0)
?
6.在A、B两座工厂之间要修建一条笔直的公路,从A地测得B地的
走向是南偏东52°,现A、B两地要同时开工,若干天后公路准确对接,则B地所修公路的走向应该是
(
)
A.北偏西52°
B.南偏东52°
C.西偏北52°
?D.西偏北52°
7.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(﹣3,3)
B.(3,2)
C.(0,3)
D.(1,3)
8.如图所示,某班教室有9排5列座位.1号同学说:“小明在我的右后方.”2号同学说:“小明在我的左后方.”3号同学说:“小明在我的左前方.”4号同学说:“小明离1号同学和3号同学的距离一样远.”根据上面4位同学的描述,可知“5号”小明的位置在( )
A.4排3列
B.4排5列
C.5排4列
D.5排5列
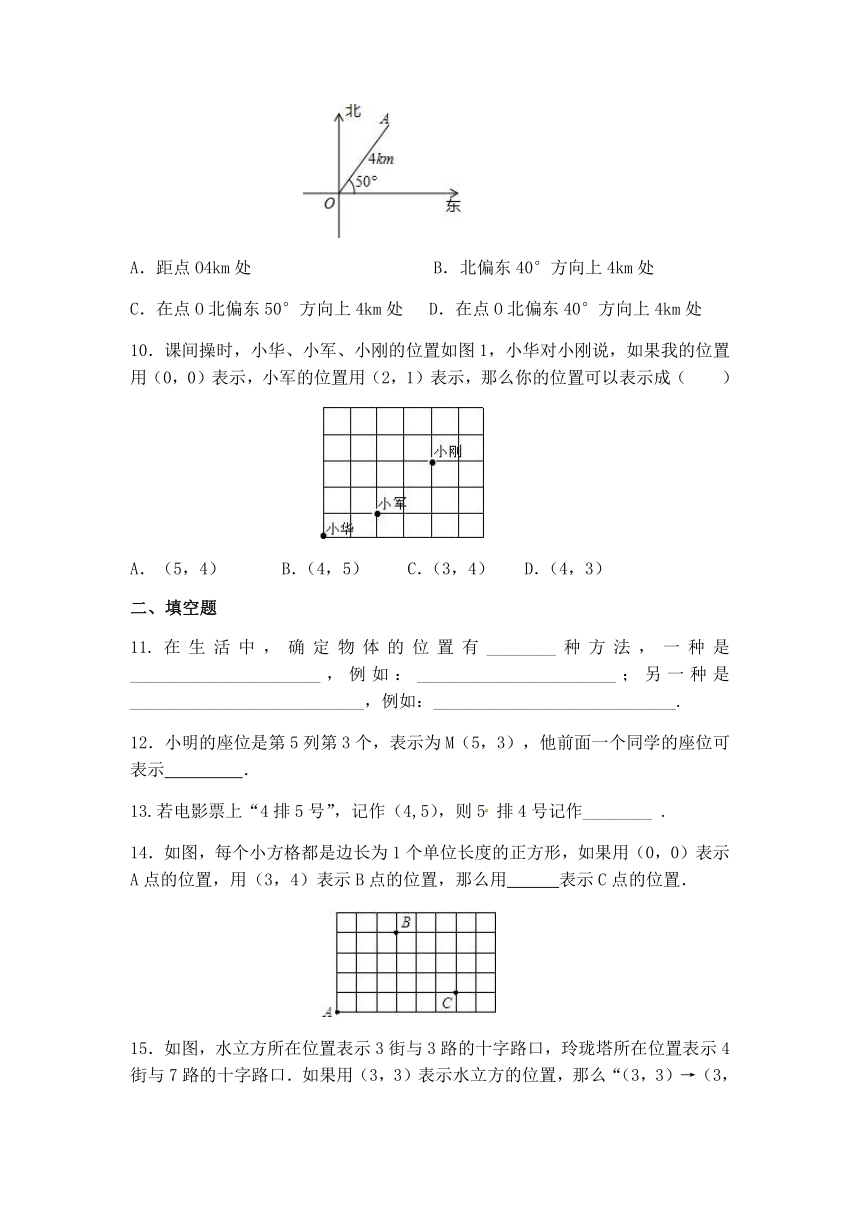
9.点A的位置如图所示,则关于点A的位置下列说法中正确的是( )
A.距点O4km处
B.北偏东40°方向上4km处
C.在点O北偏东50°方向上4km处
D.在点O北偏东40°方向上4km处
10.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )
(5,4)
B.(4,5)
C.(3,4)
D.(4,3)
二、填空题
11.在生活中,确定物体的位置有________种方法,一种是______________________,例如:_______________________;另一种是___________________________,例如:____________________________.
12.小明的座位是第5列第3个,表示为M(5,3),他前面一个同学的座位可表示
.
13.若电影票上“4排5号”,记作(4,5),则5
排4号记作________
.
14.如图,每个小方格都是边长为1个单位长度的正方形,如果用(0,0)表示A点的位置,用(3,4)表示B点的位置,那么用
表示C点的位置.
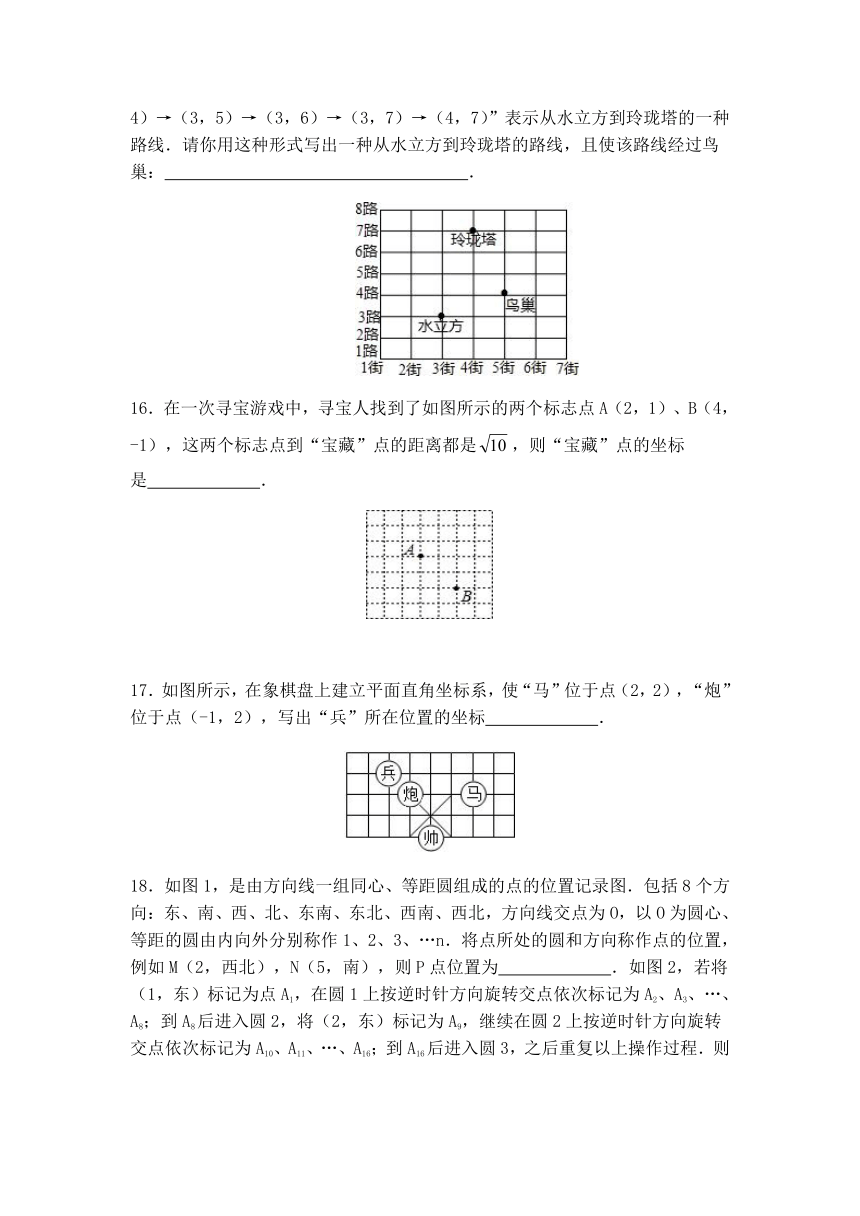
15.如图,水立方所在位置表示3街与3路的十字路口,玲珑塔所在位置表示4街与7路的十字路口.如果用(3,3)表示水立方的位置,那么“(3,3)→(3,4)→(3,5)→(3,6)→(3,7)→(4,7)”表示从水立方到玲珑塔的一种路线.请你用这种形式写出一种从水立方到玲珑塔的路线,且使该路线经过鸟巢:
.
16.在一次寻宝游戏中,寻宝人找到了如图所示的两个标志点A(2,1)、B(4,-1),这两个标志点到“宝藏”点的距离都是,则“宝藏”点的坐标是
.
17.如图所示,在象棋盘上建立平面直角坐标系,使“马”位于点(2,2),“炮”位于点(-1,2),写出“兵”所在位置的坐标
.
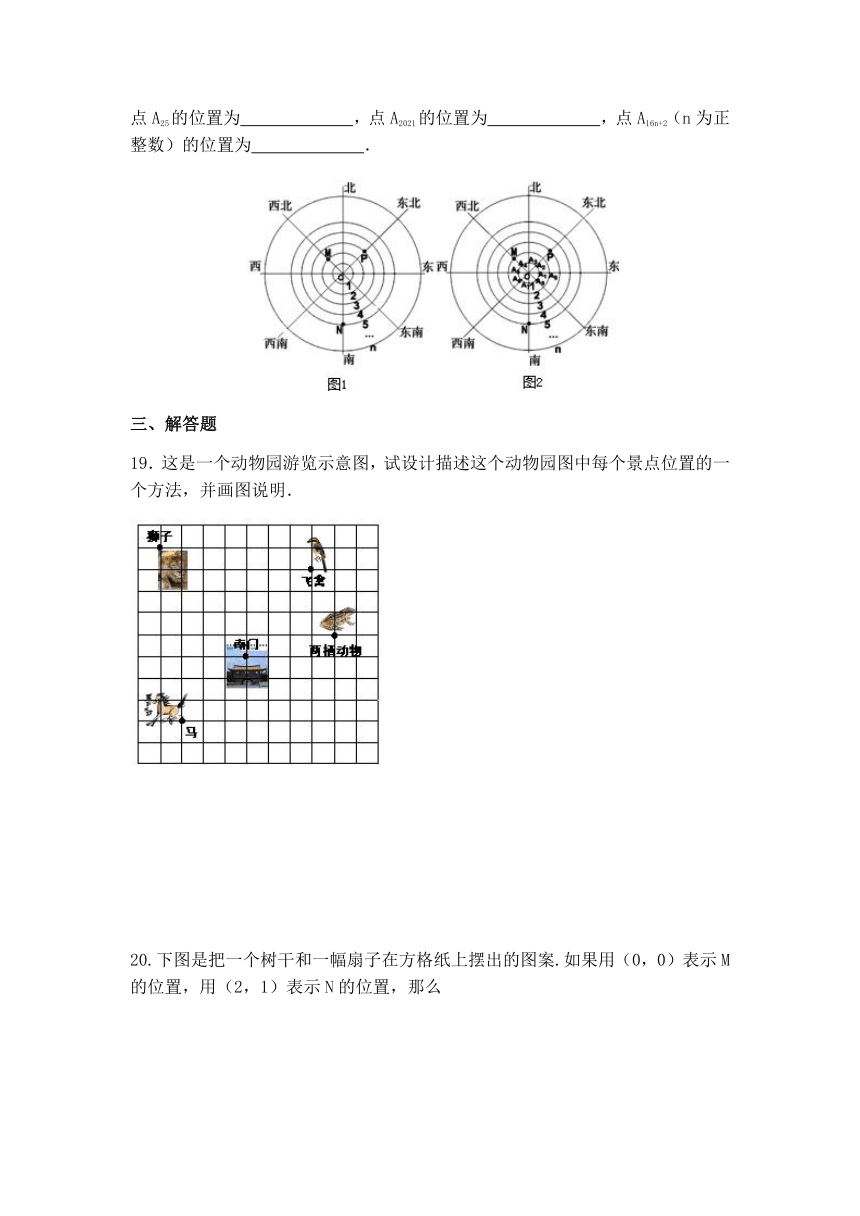
18.如图1,是由方向线一组同心、等距圆组成的点的位置记录图.包括8个方向:东、南、西、北、东南、东北、西南、西北,方向线交点为O,以O为圆心、等距的圆由内向外分别称作1、2、3、…n.将点所处的圆和方向称作点的位置,例如M(2,西北),N(5,南),则P点位置为
.如图2,若将(1,东)标记为点A1,在圆1上按逆时针方向旋转交点依次标记为A2、A3、…、A8;到A8后进入圆2,将(2,东)标记为A9,继续在圆2上按逆时针方向旋转交点依次标记为A10、A11、…、A16;到A16后进入圆3,之后重复以上操作过程.则点A25的位置为
,点A2021的位置为
,点A16n+2(n为正整数)的位置为
.
三、解答题
19.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
20.下图是把一个树干和一幅扇子在方格纸上摆出的图案.如果用(0,0)表示M的位置,用(2,1)表示N的位置,那么
图1
图2
图1中A、B、C、D、E的位置分别为_____________________________________.
(2)图2中A、B、C、D、E、F、G的位置_____________________________________.
(3)在图1和图2中分别找出(4,11)和(8,10)的位置.
21.某轮船航行到A处时观察岛B在A的北偏西75°方向上,如果轮船继续向正西航行10海里到C处,发现岛B在船的北偏西60°方向,请按1海里对应0.5
cm画出小岛与船的位置关系图示?并说明轮船向前航行过程中,距岛B的最近距离.
22.如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
23.(1)电影院在学校
偏
的方向上,距离是
米.
(2)书店在学校
偏
的方向上,距离是
米.
(3)图书馆在学校
偏
的方向上,距离是
米.
(4)李老师骑自行车从学校到邮局发邮件,每分钟走250米,需要多少分钟到达?
24.如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:
(1)一1→三2→二4→四3→五1
一
二
三
四
五
1
我
力
习
天
的
2
会
上
是
学
好
3
帅
就
更
棒
努
4
优
最
行
了
可
5
能
爱
秀
明
哥
(2)五3→二1→二3→一5→三4
(3)四5→四1→一2→三3→五2.
答案提示
1.D
2.
D.
3.B.4.A
5.D.
6.A
7.D
8.C.9.D
10.D.
11.用两个有序实数表示
电影院中座位的确定
一个方位角数字
在海上行船时,船与某岛的位置
12.(5,2).13.(5,
4)14.(6,1).
15.(3,3)→(4,3)→(5,3)→(5,4)→(5,5)→(5,6)→(5,7)→(4,7).
16.(5,2)和(1,-2).17.(-2,3).
18.(3,东北),(4,东),(253,西),(2n+1,东北).
19.此题答案不唯一,建立的直角坐标系的原点不一样,答案不一样.
解:以南门的位置作为原点建立直角坐标系,则动物们的位置分别表示为:南门(0,0),马(﹣3,﹣3);两栖动物(4,1);飞禽(3,4);狮子(﹣4,5).
20.解:(1)A(10,8),B(7,10),C(5,9),D(3,8),E(9,1)
(2)A(7,0),B(0,3),C(2,6),D(4,7),E(10,7),F(12,6),G(14,3)
(3)略
21.解:如图如图所示:最近图上距离
2.5cm,实际距离为:5海里
22.解:小王从家到工厂上班的另一条路径可为:(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
23.解:(1)南;偏东70°;400;(2)北;偏西60°;800(3)南;偏西15°400.
(4)5×200÷250=4.
答:需要4分钟到达.
24.解:(1)一1表示我,三2表示是,二4表示最,四3表示棒,五1表示的,
所以礼物为:我是最棒的;
(2)五3表示努,二1表示力,二3表示就,一5表示能,三4行,
所以礼物为:努力就能行;
(3)四5表示明,四1表示天,一2表示会,三3表示更,五2表示好,
所以礼物为:明天会更好.
3.2平面直角坐标系
一.选择题
1.以直角坐标系的原点O为圆心,以1为半径作圆.若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为α,则点P的坐标为( )
A.(cosα,1)
B.(1,sinα)
C.(sinα,cosα)
D.(cosα,sinα)
2.如图,平面直角坐标系xOy中,有A、B、C、D四点.若有一直线l经过点(﹣1,3)且与y轴垂直,则l也会经过的点是( )
A.点A
B.点B
C.点C
D.点D
3.在平面直角坐标系xOy中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(3,0),以原点O为位似中心,相似比为2,将△OAB放大,若B点的对应点B′的坐标为(﹣6,0),则A点的对应点A′坐标为( )
A.(﹣2,﹣4)
B.(﹣4,﹣2)
C.(﹣1,﹣4)
D.(1,﹣4)
4.如图,△ABC顶点C的坐标是(﹣3,2),过点C作AB上的高线CD,则垂足D点的坐标为( )
A.(2,0)
B.(﹣3,0)
C.(0,2)
D.(0,﹣3)
5.下列说法正确的是( )
A.若ab=0,则点P(a,b)表示原点
B.点(1,﹣a2)一定在第四象限
C.已知点A(1,﹣3)与点B(1,3),则直线AB平行y轴
D.已知点A(1,﹣3),AB∥y轴,且AB=4,则B点的坐标为(1,1)
6.在平面直角坐标系中,点A(x,y),B(3,4),AB=5,且AB∥x轴,则A点坐标为( )
A.(﹣3,4
)
B.(8,4
)
C.(3,9)或(﹣2,4)
D.(﹣2,4
)或(8,4)
7.如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标变为原来的,则点A的对应点A′的坐标是( )
A.(2,3)
B.(6,1)
C.(2,1)
D.(3,3)
8.如图,在平面直角坐标系中,M,N,C三点的坐标分别为(,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.
B.
C.
D.
二.填空题
9.如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,则点P的坐标为
.
10.如图,等边△OAB的边长为,则点B的坐标为
.
11.平面直角坐标系xOy中,点A(4,3),点B(3,0),点C(5,3),点E在x轴上.当CE=AB时,点E的坐标为
.
12.在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是
.
13.如图,在平面直角坐标系中,以O为圆心,6为半径画圆弧,与两坐标轴分别交于点A、B,已知点C(5,0)、D(0,3),P为AB上一点,则2PD+CP的最小值为
.
14.在平面直角坐标系中,A(﹣2,3)、B(4,4),点P是x轴上一点,且PA=PB,则点P的坐标是
.
三.解答题
15.平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|.
(1)求点A(﹣1,3)的勾股值「A」;
(2)若点B在第一象限且满足「B」=3,求满足条件的所有B点与坐标轴围成的图形的面积.
16.在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若b′=,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,2),点(﹣2,﹣5)的限变点的坐标是(﹣2,5),点(1,3)的限变点的坐标是(1,3).
(1)①点(,﹣1)的限变点的坐标是
;
②如图1,在点A(﹣2,1)、B(2,1)中有一个点是直线y=2上某一个点的限变点,这个点是
;(填“A”或“B”)
(2)如图2,已知点C(﹣2,﹣2),点D(2,2),若点P在射线OC和OD上,其限变点Q的纵坐标b的取值范围是b′≥m或b′≤n,其中m>n,令s=m﹣n,直接写出s的值.
(3)如图3,若点P在线段EF上,点E(﹣2,﹣5),点F(k,k﹣3),其限变点Q的纵坐标b′的取值范围是﹣2≤b′≤5,直接写出k的取值范围.
17.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出S△ABC.
18.如图.已知A(2,0),B(5,0),点P为圆A上一动点,圆A半径为2,以PB为边作等边△PMB,求线段AM的取值范围.
参考答案
一.选择题
1.解:作PA⊥x轴于点A,则∠POA=α,
sinα=,
∴PA=OP?sinα,
∵cosα=,
∴OA=OP?cosα.
∵OP=1,
∴PA=sinα,OA=cosα.
∴P点的坐标为(cosα,sinα)
故选:D.
2.解:如图所示:有一直线L通过点(﹣1,3)且与y轴垂直,
因为点D(0,3),
故L也会通过D点.
故选:D.
3.解:如图所示:
∵相似比为2,
∴A'(﹣2,﹣4),
故选:A.
4.解:过点C作CD垂直于x轴,垂足为D,
∵点C(﹣3,2),
∴点D横坐标与点C横坐标相等,
∴点D(﹣3,0).
故选:B.
5.解:A、若ab=0,则点P(a,b)表示在坐标轴上,故此选项错误;
B、点(1,﹣a2)一定在第四象限或x轴上,故此选项错误;
C、已知点A(1,﹣3)与点B(1,3),则直线AB平行y轴,正确;
D、已知点A(1,﹣3),AB∥y轴,且AB=4,则B点的坐标为(1,1)或(1,﹣7),故此选项错误.
故选:C.
6.解:∵AB∥x轴,B(3,4),
∴点A的纵坐标为4,
∵AB=5,
∴点A的横坐标为3﹣5=﹣2或3+5=8,
∴A点坐标为(﹣2,4
)或(8,4),
故选:D.
7.解:点A变化前的坐标为(6,3),
将纵坐标保持不变,横坐标变为原来的,
则点A的对应点A′坐标是(2,3).
故选:A.
8.解:如图,延长NM交y轴于P点,则MN⊥y轴.连接CN.
在△PAB与△NCA中,∠APB=∠CMA=90°,∠PAB=∠NCA=90°﹣∠CAN,
∴△PAB∽△NCA,
∴=,
设PA=x,则NA=PN﹣PA=3﹣x,设PB=y,
∴=,
∴y=3x﹣x2=﹣(x﹣)2+,
∵﹣1<0,≤x≤3,
∴x=时,y有最大值,此时b=1﹣=﹣,
x=3时,y有最小值0,此时b=1,
∴b的取值范围是﹣≤b≤1.
故选:B.
二.填空题
9.解:如图,设P点坐标为(x,0),
根据题意得?4?|6﹣x|=6,
解得x=3或9,
所以P点坐标为(3,0)或(9,0).
故答案为:(3,0)或(9,0).
10.解:如图,作BH⊥OA于H.
∵△OAB是等边三角形,BH⊥OA,
∴OH=AH=,∠BOH=60°,
∴BH=OH?tan60°=3,
∴B(,3),
故答案为(,3)
11.解:∵点A(4,3),点C(5,3),
∴AC∥x轴,AC=1,
连接AC,过C作CE∥AB交x轴于E,
∴AB=CE,BE=AC=1,
∵点B(3,0),
∴E(4,0),
以C为圆心,CE为半径画弧交x轴于E′,
则CE=CE′=AB,
过C作CD⊥x轴于D,
∴DE=DE′=1,
∴E′(6,0),
∴当CE=AB时,点E的坐标为(4,0)或(6,0),
故答案为:(4,0)或(6,0).
12.解:∵点M(1,x)与点N(1,3)之间的距离是5,
∴|x﹣3|=5,
解得x=﹣2或8.
故答案为:﹣2或8.
13.
解:如图所示,
在y轴上找一点E,使AE=OA=6,
∵D(0,3),
∴OD=3
∵∠DOP=∠POE,==
∴△DOP∽△POE
∴==
∴PE=2PD
∴2PD+CP=PE+CP
当点C,P,E三点共线时,
2PD+CP的值最小,
∴2PD+CP的最小值=CE===13.
故答案为13.
14.解:设P(x,0),
∵PA=PB,
∴(x+2)2+(0﹣3)2=(x﹣4)2+(0﹣4)2,
∴x=,
故答案为(,0).
三.解答题
15.解:(1)「A」=|﹣1|+|3|=4,
(2)设B(x,y),由「B」=3且在第一象限知,x+y=3(x>0,y>0),
即:y=﹣x+3(x>0,y>0).
故所有点B与坐标轴围成的图形如图所示的三角形,
故其面积为×3×3=.
16.(1)①∵a=<2,
∴b′=|b|=|﹣1|=1,
∴坐标为(,1).
故答案为(,1).
②s=3.
∵对于限变点来说,横坐标保持不变,
∴限变点A(﹣2,1)对应的原来点的坐标为:(﹣2,1)或(﹣2,﹣1),
限变点B(2,1]对应的原来点的坐标为:(2.2),
∵(2,2)满足y=2,
∴这个点是B,
故答案为:B;
(
2)∵点C的坐标为(﹣2,﹣2),
∴OC的关系式为:y=x(x≤0),
∵点D的坐标为(2,﹣2),
∴OD的关系式为:y=﹣x(x≥0),
∴点P满足的关系式为:y=,
当x≥2时:b'=一x﹣1,
当0<x<2时:b'=﹣x﹣1,
当x≤0时,b=|x|=﹣x,
图象如图1所示,
通过图象可以得出:当x≥2时,b'≤﹣3,n=﹣3,
当x<2时,b'≥0,
∴m=0,
∴s=m﹣n=0﹣(﹣3)=3;
(3)设线段E的关系式为:y=ax+c(a≠0,﹣2≤x≤k,k>﹣2),
把E(﹣2,﹣5),F(k,k﹣3)代入,
得,
解得,
∴线段EP的关系式为y=x一3(﹣2≤x≤k,k>﹣2),
∴线段E上的点P的限变点Q的纵坐标满足的关系式b'=
,
图象如图2所示:
当x=2时,b'取最小值,b'=2﹣4=﹣2,
当b'=5时,
x﹣4=5或﹣x+3=5,解得:x=9或x=﹣2,
当b'=1时,
x﹣4=1,解得:x=5,
∵﹣2≤b'<5,
∴由图象可知,k的取值范围是:5≤k≤9.
17.解:(1)A(﹣1,﹣1),B(4,2),C(1,3);
(2)S△ABC=4×5﹣=7.
18.解:要求AM的取值范围,则先确定M点运动轨迹.
如图,由等边三角形联想共顶点的双等边结构,
可构造和△PBM共顶点B的等边△ABH,
则△APB≌△HBM?HM=PA=2,
所以点M运动轨迹为以H为圆心,半径为2的圆H上的点.
当点P1(4,0)时,点M与E重合,
当P2(0,0)时,点M与F重合,
此时△BFO和△BEP1都是等边三角形,
所以BF=BO=5,BE=BP1=1,
所以BH=BA=AH=3,
AM过圆心时取得相应最大和最小值.
点M运动轨迹为以H为圆心,半径为2的圆H上的点.
AM过圆心时取得相应最大和最小值.
因为圆A的半径为2,圆H的半径为2,
当点A和点M在一条直线上时,HA=3,
那么AM的最大值为3+2=5;
最小值为3﹣2=1.
所以线段AM的取值范围是:1≤AM≤5.
3.3
轴对称与坐标变化
一.选择题
1.在平面直角坐标系中,将点(﹣1,5)向左平移2个单位长度后得到点P,则点P的坐标是( )
A.(﹣1,3)
B.(﹣3,5)
C.(﹣1,7)
D.(1,5)
2.在平面直角坐标系中,将点A(﹣2,6)沿x轴向右平移5个单位后的对应点A'的坐标为( )
A.(3,6)
B.(﹣2,11)
C.(﹣7,6)
D.(﹣2,1)
3.将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是( )
A.(﹣1,﹣1)
B.(﹣1,3)
C.(5,﹣1)
D.(5,3)
4.在平面直角坐标系中,点A'(2,﹣2)可以由点A(﹣2,3)通过两次平移得到,则正确的是( )
A.先向左平移4个单位长度,再向上平移5个单位长度
B.先向右平移4个单位长度,再向上平移5个单位长度
C.先向左平移4个单位长度,再向下平移5个单位长度
D.先向右平移4个单位长度,再向下平移5个单位长度
5.如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,﹣1)对应点的坐标为( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
6.已知A(1,﹣3),B(2,﹣1),现将线段AB平移至A1B1,如果点A1(a,﹣1),B1(﹣2,b),那么a+b的值是( )
A.6
B.﹣1
C.2
D.﹣2
7.把点A(2,)向上平移2个单位得到点A′坐标为( )
A.(2,﹣)
B.(2,)
C.(2,﹣3
)
D.(2,3
)
8.将点P(m+2,2﹣m)向左平移1个单位长度到P',且P'在y轴上,那么点P的坐标是( )
A.(1,3)
B.(3,﹣1)
C.(﹣1,5)
D.(3,1)
9.在平面直角坐标系中,将点P(﹣4,﹣2)先向上平移3个单位长度,再向左平移2个单位长度后得到的点的坐标是( )
A.(﹣6,1)
B.(﹣2,1)
C.(﹣1,﹣4)
D.(﹣1,0)
10.如图,在平面直角坐标系中,线段AB的两个端点都在格点上,如果先将线段AB向右平移两个单位,得到线段A′B′,其中点A、B的对应点分别为点A′、B′,然后将线段A′B′绕点P顺时针旋转得到线段A′′B′′,其中点A′、B′的对应点分别为点A′′、B′′,则旋转中心点P的坐标为( )
A.(1,0)
B.(0,2)
C.(3,1)
D.(4,﹣1)
二.填空题
11.在平面直角坐标系中,将点A(﹣1,﹣2)向右平移7个单位长度,得到点B,则点B的坐标为
.
12.如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B对应点B1的坐标为
.
13.若点A(2x﹣1,5)和点B(4,y+3)关于点(﹣3,2)对称,那么点A在第
象限.
14.如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b=
.
15.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是
.
A.(﹣2,1)
B.(﹣1,1)
C.(1,﹣2)
D.(﹣1,﹣2)
三.解答题
16.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′,C′的坐标;
(2)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
17.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(2,4),B(1,1),(3,2).
(1)在平面直角坐标系中画出△ABC,并判断三角形的形状(不写理由);
(2)平移△ABC,使点A与点O重合,写出点B、点C平移后的所得点的坐标,并描述这个平移过程.
18.如图在直角坐标系中,△ABC为Rt△,A、C两点分别在x轴、y轴上,∠B=90°,B点坐标为(1,3)将△ABC沿AC翻折,B点落在D点位置,AD交y轴于点E,求D点坐标.
参考答案
1-5
BABDD
6-10
DDAAB
11.(6,﹣2)
12.(﹣1,0)
13.二
14.﹣5
15.B
16.解:(1)如图,△A′B′C′即为所求,A′(0,4),B′(﹣1,1),C′(3,1).
(2)设P(0,m),
由题意:×4×|m+2|=×4×3,
解得m=1或﹣5,
∴P(0,1)或(0,﹣5).
17.解:(1)如图,△ABC即为所求,△ABC
等腰直角三角形.
(2)平移后的△OB′C′即为所求,B′(﹣1,﹣3),C′(1,﹣2),△ABC向下平移4个单位,向左平移2个单位得到△OB′C′.
18.解:如图,过D作DH⊥OC于H.
∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=CB=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE(AAS),
∴OE=DE,OA=CD=1,
设OE=x,那么CE=3﹣x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(3﹣x)2=x2+12,
∴x=.
∴CE=,DE=,
又∵DH⊥CE
∴CE×DH=CD×DE,
∴DH==,
∴Rt△CDH中,CH===
∴OH=3﹣=
∵点D在第二象限,
∴点D的坐标为(﹣,).
3.1确定位置
一、选择题
1.根据下列表述,能确定位置的是( )
A.红星电影院2排
B.北京市四环路
C.北偏东30°
D.东经118°,北纬40°
2.海事救灾船前去救援某海域失火的轮船,需要确定(
).
A.方位角
B.距离
C.失火轮船的船长
D.方位角和距离
3.电影院的第3排第6座表示为(3,6).若某同学的座位号为(4,2),那么该同学的位置是( )
A.第2排第4座
B.第4排第2座
C.第4座第4排
D.无法确定
4.如图是丁丁画的一张脸的示意图,如果用(0,2)表示靠左边的眼睛,用(2,2)表示靠右边的眼睛,那么嘴的位置可以表示成( )
A.(1,0)
B.(﹣1,0)
C.(﹣1,1)
D.(1,﹣1)
5.如图所示,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,小明走下面哪条线路不能到达学校(
).
A.(0,4)→(0,0)→(4,0)
B.(0,4)→(4,4)→(4,0)
C.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)
D.(0,4)→(3,4)→(4,2)→(4,0)
?
6.在A、B两座工厂之间要修建一条笔直的公路,从A地测得B地的
走向是南偏东52°,现A、B两地要同时开工,若干天后公路准确对接,则B地所修公路的走向应该是
(
)
A.北偏西52°
B.南偏东52°
C.西偏北52°
?D.西偏北52°
7.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(﹣3,3)
B.(3,2)
C.(0,3)
D.(1,3)
8.如图所示,某班教室有9排5列座位.1号同学说:“小明在我的右后方.”2号同学说:“小明在我的左后方.”3号同学说:“小明在我的左前方.”4号同学说:“小明离1号同学和3号同学的距离一样远.”根据上面4位同学的描述,可知“5号”小明的位置在( )
A.4排3列
B.4排5列
C.5排4列
D.5排5列
9.点A的位置如图所示,则关于点A的位置下列说法中正确的是( )
A.距点O4km处
B.北偏东40°方向上4km处
C.在点O北偏东50°方向上4km处
D.在点O北偏东40°方向上4km处
10.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )
(5,4)
B.(4,5)
C.(3,4)
D.(4,3)
二、填空题
11.在生活中,确定物体的位置有________种方法,一种是______________________,例如:_______________________;另一种是___________________________,例如:____________________________.
12.小明的座位是第5列第3个,表示为M(5,3),他前面一个同学的座位可表示
.
13.若电影票上“4排5号”,记作(4,5),则5
排4号记作________
.
14.如图,每个小方格都是边长为1个单位长度的正方形,如果用(0,0)表示A点的位置,用(3,4)表示B点的位置,那么用
表示C点的位置.
15.如图,水立方所在位置表示3街与3路的十字路口,玲珑塔所在位置表示4街与7路的十字路口.如果用(3,3)表示水立方的位置,那么“(3,3)→(3,4)→(3,5)→(3,6)→(3,7)→(4,7)”表示从水立方到玲珑塔的一种路线.请你用这种形式写出一种从水立方到玲珑塔的路线,且使该路线经过鸟巢:
.
16.在一次寻宝游戏中,寻宝人找到了如图所示的两个标志点A(2,1)、B(4,-1),这两个标志点到“宝藏”点的距离都是,则“宝藏”点的坐标是
.
17.如图所示,在象棋盘上建立平面直角坐标系,使“马”位于点(2,2),“炮”位于点(-1,2),写出“兵”所在位置的坐标
.
18.如图1,是由方向线一组同心、等距圆组成的点的位置记录图.包括8个方向:东、南、西、北、东南、东北、西南、西北,方向线交点为O,以O为圆心、等距的圆由内向外分别称作1、2、3、…n.将点所处的圆和方向称作点的位置,例如M(2,西北),N(5,南),则P点位置为
.如图2,若将(1,东)标记为点A1,在圆1上按逆时针方向旋转交点依次标记为A2、A3、…、A8;到A8后进入圆2,将(2,东)标记为A9,继续在圆2上按逆时针方向旋转交点依次标记为A10、A11、…、A16;到A16后进入圆3,之后重复以上操作过程.则点A25的位置为
,点A2021的位置为
,点A16n+2(n为正整数)的位置为
.
三、解答题
19.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
20.下图是把一个树干和一幅扇子在方格纸上摆出的图案.如果用(0,0)表示M的位置,用(2,1)表示N的位置,那么
图1
图2
图1中A、B、C、D、E的位置分别为_____________________________________.
(2)图2中A、B、C、D、E、F、G的位置_____________________________________.
(3)在图1和图2中分别找出(4,11)和(8,10)的位置.
21.某轮船航行到A处时观察岛B在A的北偏西75°方向上,如果轮船继续向正西航行10海里到C处,发现岛B在船的北偏西60°方向,请按1海里对应0.5
cm画出小岛与船的位置关系图示?并说明轮船向前航行过程中,距岛B的最近距离.
22.如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
23.(1)电影院在学校
偏
的方向上,距离是
米.
(2)书店在学校
偏
的方向上,距离是
米.
(3)图书馆在学校
偏
的方向上,距离是
米.
(4)李老师骑自行车从学校到邮局发邮件,每分钟走250米,需要多少分钟到达?
24.如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:
(1)一1→三2→二4→四3→五1
一
二
三
四
五
1
我
力
习
天
的
2
会
上
是
学
好
3
帅
就
更
棒
努
4
优
最
行
了
可
5
能
爱
秀
明
哥
(2)五3→二1→二3→一5→三4
(3)四5→四1→一2→三3→五2.
答案提示
1.D
2.
D.
3.B.4.A
5.D.
6.A
7.D
8.C.9.D
10.D.
11.用两个有序实数表示
电影院中座位的确定
一个方位角数字
在海上行船时,船与某岛的位置
12.(5,2).13.(5,
4)14.(6,1).
15.(3,3)→(4,3)→(5,3)→(5,4)→(5,5)→(5,6)→(5,7)→(4,7).
16.(5,2)和(1,-2).17.(-2,3).
18.(3,东北),(4,东),(253,西),(2n+1,东北).
19.此题答案不唯一,建立的直角坐标系的原点不一样,答案不一样.
解:以南门的位置作为原点建立直角坐标系,则动物们的位置分别表示为:南门(0,0),马(﹣3,﹣3);两栖动物(4,1);飞禽(3,4);狮子(﹣4,5).
20.解:(1)A(10,8),B(7,10),C(5,9),D(3,8),E(9,1)
(2)A(7,0),B(0,3),C(2,6),D(4,7),E(10,7),F(12,6),G(14,3)
(3)略
21.解:如图如图所示:最近图上距离
2.5cm,实际距离为:5海里
22.解:小王从家到工厂上班的另一条路径可为:(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
23.解:(1)南;偏东70°;400;(2)北;偏西60°;800(3)南;偏西15°400.
(4)5×200÷250=4.
答:需要4分钟到达.
24.解:(1)一1表示我,三2表示是,二4表示最,四3表示棒,五1表示的,
所以礼物为:我是最棒的;
(2)五3表示努,二1表示力,二3表示就,一5表示能,三4行,
所以礼物为:努力就能行;
(3)四5表示明,四1表示天,一2表示会,三3表示更,五2表示好,
所以礼物为:明天会更好.
3.2平面直角坐标系
一.选择题
1.以直角坐标系的原点O为圆心,以1为半径作圆.若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为α,则点P的坐标为( )
A.(cosα,1)
B.(1,sinα)
C.(sinα,cosα)
D.(cosα,sinα)
2.如图,平面直角坐标系xOy中,有A、B、C、D四点.若有一直线l经过点(﹣1,3)且与y轴垂直,则l也会经过的点是( )
A.点A
B.点B
C.点C
D.点D
3.在平面直角坐标系xOy中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(3,0),以原点O为位似中心,相似比为2,将△OAB放大,若B点的对应点B′的坐标为(﹣6,0),则A点的对应点A′坐标为( )
A.(﹣2,﹣4)
B.(﹣4,﹣2)
C.(﹣1,﹣4)
D.(1,﹣4)
4.如图,△ABC顶点C的坐标是(﹣3,2),过点C作AB上的高线CD,则垂足D点的坐标为( )
A.(2,0)
B.(﹣3,0)
C.(0,2)
D.(0,﹣3)
5.下列说法正确的是( )
A.若ab=0,则点P(a,b)表示原点
B.点(1,﹣a2)一定在第四象限
C.已知点A(1,﹣3)与点B(1,3),则直线AB平行y轴
D.已知点A(1,﹣3),AB∥y轴,且AB=4,则B点的坐标为(1,1)
6.在平面直角坐标系中,点A(x,y),B(3,4),AB=5,且AB∥x轴,则A点坐标为( )
A.(﹣3,4
)
B.(8,4
)
C.(3,9)或(﹣2,4)
D.(﹣2,4
)或(8,4)
7.如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标变为原来的,则点A的对应点A′的坐标是( )
A.(2,3)
B.(6,1)
C.(2,1)
D.(3,3)
8.如图,在平面直角坐标系中,M,N,C三点的坐标分别为(,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.
B.
C.
D.
二.填空题
9.如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,则点P的坐标为
.
10.如图,等边△OAB的边长为,则点B的坐标为
.
11.平面直角坐标系xOy中,点A(4,3),点B(3,0),点C(5,3),点E在x轴上.当CE=AB时,点E的坐标为
.
12.在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是
.
13.如图,在平面直角坐标系中,以O为圆心,6为半径画圆弧,与两坐标轴分别交于点A、B,已知点C(5,0)、D(0,3),P为AB上一点,则2PD+CP的最小值为
.
14.在平面直角坐标系中,A(﹣2,3)、B(4,4),点P是x轴上一点,且PA=PB,则点P的坐标是
.
三.解答题
15.平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|.
(1)求点A(﹣1,3)的勾股值「A」;
(2)若点B在第一象限且满足「B」=3,求满足条件的所有B点与坐标轴围成的图形的面积.
16.在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若b′=,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,2),点(﹣2,﹣5)的限变点的坐标是(﹣2,5),点(1,3)的限变点的坐标是(1,3).
(1)①点(,﹣1)的限变点的坐标是
;
②如图1,在点A(﹣2,1)、B(2,1)中有一个点是直线y=2上某一个点的限变点,这个点是
;(填“A”或“B”)
(2)如图2,已知点C(﹣2,﹣2),点D(2,2),若点P在射线OC和OD上,其限变点Q的纵坐标b的取值范围是b′≥m或b′≤n,其中m>n,令s=m﹣n,直接写出s的值.
(3)如图3,若点P在线段EF上,点E(﹣2,﹣5),点F(k,k﹣3),其限变点Q的纵坐标b′的取值范围是﹣2≤b′≤5,直接写出k的取值范围.
17.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出S△ABC.
18.如图.已知A(2,0),B(5,0),点P为圆A上一动点,圆A半径为2,以PB为边作等边△PMB,求线段AM的取值范围.
参考答案
一.选择题
1.解:作PA⊥x轴于点A,则∠POA=α,
sinα=,
∴PA=OP?sinα,
∵cosα=,
∴OA=OP?cosα.
∵OP=1,
∴PA=sinα,OA=cosα.
∴P点的坐标为(cosα,sinα)
故选:D.
2.解:如图所示:有一直线L通过点(﹣1,3)且与y轴垂直,
因为点D(0,3),
故L也会通过D点.
故选:D.
3.解:如图所示:
∵相似比为2,
∴A'(﹣2,﹣4),
故选:A.
4.解:过点C作CD垂直于x轴,垂足为D,
∵点C(﹣3,2),
∴点D横坐标与点C横坐标相等,
∴点D(﹣3,0).
故选:B.
5.解:A、若ab=0,则点P(a,b)表示在坐标轴上,故此选项错误;
B、点(1,﹣a2)一定在第四象限或x轴上,故此选项错误;
C、已知点A(1,﹣3)与点B(1,3),则直线AB平行y轴,正确;
D、已知点A(1,﹣3),AB∥y轴,且AB=4,则B点的坐标为(1,1)或(1,﹣7),故此选项错误.
故选:C.
6.解:∵AB∥x轴,B(3,4),
∴点A的纵坐标为4,
∵AB=5,
∴点A的横坐标为3﹣5=﹣2或3+5=8,
∴A点坐标为(﹣2,4
)或(8,4),
故选:D.
7.解:点A变化前的坐标为(6,3),
将纵坐标保持不变,横坐标变为原来的,
则点A的对应点A′坐标是(2,3).
故选:A.
8.解:如图,延长NM交y轴于P点,则MN⊥y轴.连接CN.
在△PAB与△NCA中,∠APB=∠CMA=90°,∠PAB=∠NCA=90°﹣∠CAN,
∴△PAB∽△NCA,
∴=,
设PA=x,则NA=PN﹣PA=3﹣x,设PB=y,
∴=,
∴y=3x﹣x2=﹣(x﹣)2+,
∵﹣1<0,≤x≤3,
∴x=时,y有最大值,此时b=1﹣=﹣,
x=3时,y有最小值0,此时b=1,
∴b的取值范围是﹣≤b≤1.
故选:B.
二.填空题
9.解:如图,设P点坐标为(x,0),
根据题意得?4?|6﹣x|=6,
解得x=3或9,
所以P点坐标为(3,0)或(9,0).
故答案为:(3,0)或(9,0).
10.解:如图,作BH⊥OA于H.
∵△OAB是等边三角形,BH⊥OA,
∴OH=AH=,∠BOH=60°,
∴BH=OH?tan60°=3,
∴B(,3),
故答案为(,3)
11.解:∵点A(4,3),点C(5,3),
∴AC∥x轴,AC=1,
连接AC,过C作CE∥AB交x轴于E,
∴AB=CE,BE=AC=1,
∵点B(3,0),
∴E(4,0),
以C为圆心,CE为半径画弧交x轴于E′,
则CE=CE′=AB,
过C作CD⊥x轴于D,
∴DE=DE′=1,
∴E′(6,0),
∴当CE=AB时,点E的坐标为(4,0)或(6,0),
故答案为:(4,0)或(6,0).
12.解:∵点M(1,x)与点N(1,3)之间的距离是5,
∴|x﹣3|=5,
解得x=﹣2或8.
故答案为:﹣2或8.
13.
解:如图所示,
在y轴上找一点E,使AE=OA=6,
∵D(0,3),
∴OD=3
∵∠DOP=∠POE,==
∴△DOP∽△POE
∴==
∴PE=2PD
∴2PD+CP=PE+CP
当点C,P,E三点共线时,
2PD+CP的值最小,
∴2PD+CP的最小值=CE===13.
故答案为13.
14.解:设P(x,0),
∵PA=PB,
∴(x+2)2+(0﹣3)2=(x﹣4)2+(0﹣4)2,
∴x=,
故答案为(,0).
三.解答题
15.解:(1)「A」=|﹣1|+|3|=4,
(2)设B(x,y),由「B」=3且在第一象限知,x+y=3(x>0,y>0),
即:y=﹣x+3(x>0,y>0).
故所有点B与坐标轴围成的图形如图所示的三角形,
故其面积为×3×3=.
16.(1)①∵a=<2,
∴b′=|b|=|﹣1|=1,
∴坐标为(,1).
故答案为(,1).
②s=3.
∵对于限变点来说,横坐标保持不变,
∴限变点A(﹣2,1)对应的原来点的坐标为:(﹣2,1)或(﹣2,﹣1),
限变点B(2,1]对应的原来点的坐标为:(2.2),
∵(2,2)满足y=2,
∴这个点是B,
故答案为:B;
(
2)∵点C的坐标为(﹣2,﹣2),
∴OC的关系式为:y=x(x≤0),
∵点D的坐标为(2,﹣2),
∴OD的关系式为:y=﹣x(x≥0),
∴点P满足的关系式为:y=,
当x≥2时:b'=一x﹣1,
当0<x<2时:b'=﹣x﹣1,
当x≤0时,b=|x|=﹣x,
图象如图1所示,
通过图象可以得出:当x≥2时,b'≤﹣3,n=﹣3,
当x<2时,b'≥0,
∴m=0,
∴s=m﹣n=0﹣(﹣3)=3;
(3)设线段E的关系式为:y=ax+c(a≠0,﹣2≤x≤k,k>﹣2),
把E(﹣2,﹣5),F(k,k﹣3)代入,
得,
解得,
∴线段EP的关系式为y=x一3(﹣2≤x≤k,k>﹣2),
∴线段E上的点P的限变点Q的纵坐标满足的关系式b'=
,
图象如图2所示:
当x=2时,b'取最小值,b'=2﹣4=﹣2,
当b'=5时,
x﹣4=5或﹣x+3=5,解得:x=9或x=﹣2,
当b'=1时,
x﹣4=1,解得:x=5,
∵﹣2≤b'<5,
∴由图象可知,k的取值范围是:5≤k≤9.
17.解:(1)A(﹣1,﹣1),B(4,2),C(1,3);
(2)S△ABC=4×5﹣=7.
18.解:要求AM的取值范围,则先确定M点运动轨迹.
如图,由等边三角形联想共顶点的双等边结构,
可构造和△PBM共顶点B的等边△ABH,
则△APB≌△HBM?HM=PA=2,
所以点M运动轨迹为以H为圆心,半径为2的圆H上的点.
当点P1(4,0)时,点M与E重合,
当P2(0,0)时,点M与F重合,
此时△BFO和△BEP1都是等边三角形,
所以BF=BO=5,BE=BP1=1,
所以BH=BA=AH=3,
AM过圆心时取得相应最大和最小值.
点M运动轨迹为以H为圆心,半径为2的圆H上的点.
AM过圆心时取得相应最大和最小值.
因为圆A的半径为2,圆H的半径为2,
当点A和点M在一条直线上时,HA=3,
那么AM的最大值为3+2=5;
最小值为3﹣2=1.
所以线段AM的取值范围是:1≤AM≤5.
3.3
轴对称与坐标变化
一.选择题
1.在平面直角坐标系中,将点(﹣1,5)向左平移2个单位长度后得到点P,则点P的坐标是( )
A.(﹣1,3)
B.(﹣3,5)
C.(﹣1,7)
D.(1,5)
2.在平面直角坐标系中,将点A(﹣2,6)沿x轴向右平移5个单位后的对应点A'的坐标为( )
A.(3,6)
B.(﹣2,11)
C.(﹣7,6)
D.(﹣2,1)
3.将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是( )
A.(﹣1,﹣1)
B.(﹣1,3)
C.(5,﹣1)
D.(5,3)
4.在平面直角坐标系中,点A'(2,﹣2)可以由点A(﹣2,3)通过两次平移得到,则正确的是( )
A.先向左平移4个单位长度,再向上平移5个单位长度
B.先向右平移4个单位长度,再向上平移5个单位长度
C.先向左平移4个单位长度,再向下平移5个单位长度
D.先向右平移4个单位长度,再向下平移5个单位长度
5.如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,﹣1)对应点的坐标为( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
6.已知A(1,﹣3),B(2,﹣1),现将线段AB平移至A1B1,如果点A1(a,﹣1),B1(﹣2,b),那么a+b的值是( )
A.6
B.﹣1
C.2
D.﹣2
7.把点A(2,)向上平移2个单位得到点A′坐标为( )
A.(2,﹣)
B.(2,)
C.(2,﹣3
)
D.(2,3
)
8.将点P(m+2,2﹣m)向左平移1个单位长度到P',且P'在y轴上,那么点P的坐标是( )
A.(1,3)
B.(3,﹣1)
C.(﹣1,5)
D.(3,1)
9.在平面直角坐标系中,将点P(﹣4,﹣2)先向上平移3个单位长度,再向左平移2个单位长度后得到的点的坐标是( )
A.(﹣6,1)
B.(﹣2,1)
C.(﹣1,﹣4)
D.(﹣1,0)
10.如图,在平面直角坐标系中,线段AB的两个端点都在格点上,如果先将线段AB向右平移两个单位,得到线段A′B′,其中点A、B的对应点分别为点A′、B′,然后将线段A′B′绕点P顺时针旋转得到线段A′′B′′,其中点A′、B′的对应点分别为点A′′、B′′,则旋转中心点P的坐标为( )
A.(1,0)
B.(0,2)
C.(3,1)
D.(4,﹣1)
二.填空题
11.在平面直角坐标系中,将点A(﹣1,﹣2)向右平移7个单位长度,得到点B,则点B的坐标为
.
12.如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B对应点B1的坐标为
.
13.若点A(2x﹣1,5)和点B(4,y+3)关于点(﹣3,2)对称,那么点A在第
象限.
14.如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b=
.
15.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是
.
A.(﹣2,1)
B.(﹣1,1)
C.(1,﹣2)
D.(﹣1,﹣2)
三.解答题
16.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′,C′的坐标;
(2)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
17.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(2,4),B(1,1),(3,2).
(1)在平面直角坐标系中画出△ABC,并判断三角形的形状(不写理由);
(2)平移△ABC,使点A与点O重合,写出点B、点C平移后的所得点的坐标,并描述这个平移过程.
18.如图在直角坐标系中,△ABC为Rt△,A、C两点分别在x轴、y轴上,∠B=90°,B点坐标为(1,3)将△ABC沿AC翻折,B点落在D点位置,AD交y轴于点E,求D点坐标.
参考答案
1-5
BABDD
6-10
DDAAB
11.(6,﹣2)
12.(﹣1,0)
13.二
14.﹣5
15.B
16.解:(1)如图,△A′B′C′即为所求,A′(0,4),B′(﹣1,1),C′(3,1).
(2)设P(0,m),
由题意:×4×|m+2|=×4×3,
解得m=1或﹣5,
∴P(0,1)或(0,﹣5).
17.解:(1)如图,△ABC即为所求,△ABC
等腰直角三角形.
(2)平移后的△OB′C′即为所求,B′(﹣1,﹣3),C′(1,﹣2),△ABC向下平移4个单位,向左平移2个单位得到△OB′C′.
18.解:如图,过D作DH⊥OC于H.
∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=CB=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE(AAS),
∴OE=DE,OA=CD=1,
设OE=x,那么CE=3﹣x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(3﹣x)2=x2+12,
∴x=.
∴CE=,DE=,
又∵DH⊥CE
∴CE×DH=CD×DE,
∴DH==,
∴Rt△CDH中,CH===
∴OH=3﹣=
∵点D在第二象限,
∴点D的坐标为(﹣,).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
