湘教版九年级数学下册第2章 圆中考演练(word版含答案)
文档属性
| 名称 | 湘教版九年级数学下册第2章 圆中考演练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 251.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 21:42:53 | ||
图片预览




文档简介
第2章 圆
中考演练
一、选择题
1.[2020·淮安]
如图1,点A,B,C在☉O上,∠ACB=54°,则∠ABO的度数是
( )
图1
A.54°
B.27°
C.36°
D.108°
2.[2020·张家界]
如图2,四边形ABCD为☉O的内接四边形,∠BCD=120°,则∠BOD的度数为
( )
图2
A.100°
B.110°
C.120°
D.130°
3.[2020·温州]
如图3,菱形OABC的顶点A,B,C都在☉O上,过点B作☉O的切线交OA的延长线于点D.若☉O的半径为1,则BD的长为
( )
图3
A.1
B.2
C.
D.
4.[2020·湘西州]
如图4,PA,PB为☉O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交☉O于点D.下列结论不一定成立的是
( )
图4
A.△BPA为等腰三角形
B.AB与PD互相垂直平分
C.点A,B都在以PO为直径的圆上
D.PC为△BPA的边AB上的中线
5.[2020·扬州]
如图5,由边长均为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin∠ADC的值为
( )
图5
A.
B.
C.
D.
6.[2020·黔东南州]
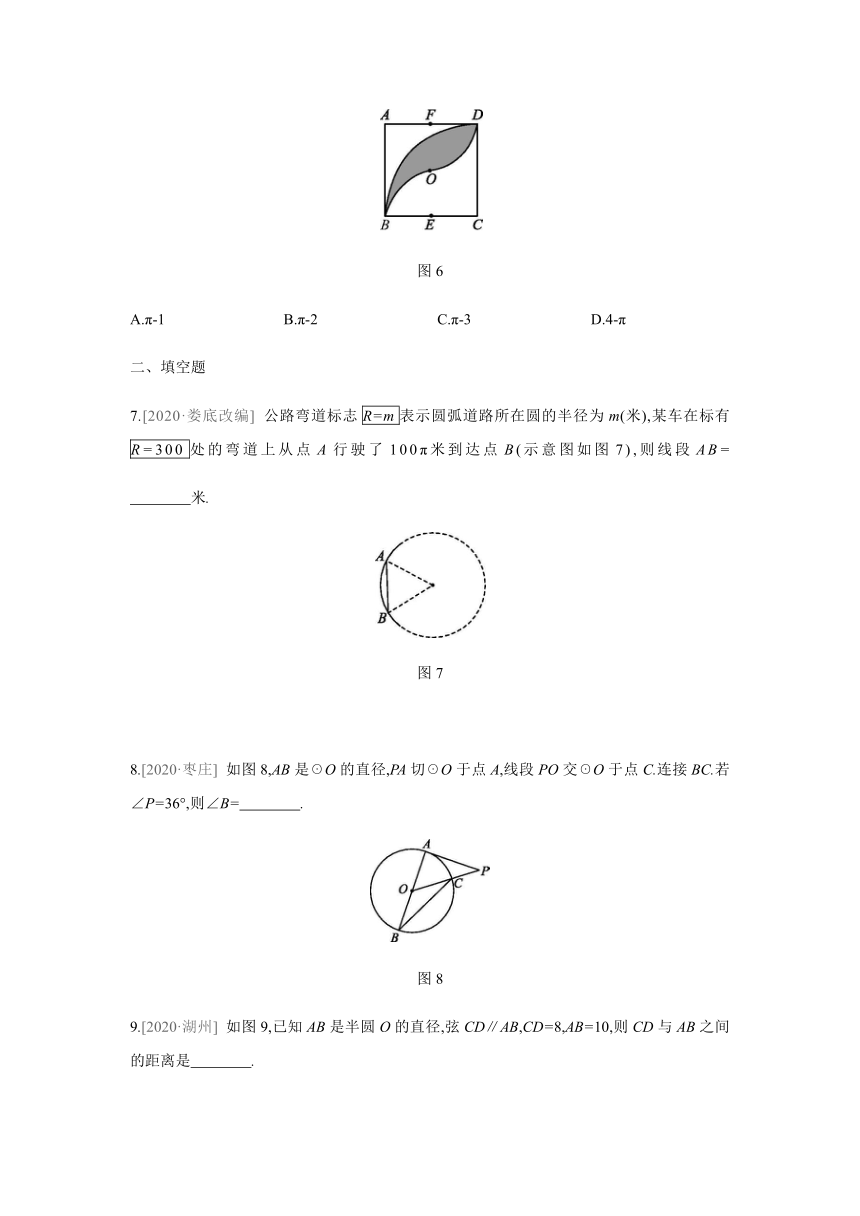
如图6,正方形ABCD的边长为2,O为对角线的交点,E,F分别为BC,AD的中点.以点C为圆心,2为半径作圆弧,再分别以点E,F为圆心,1为半径作圆弧,,则图中阴影部分的面积为
( )
图6
A.π-1
B.π-2
C.π-3
D.4-π
二、填空题
7.[2020·娄底改编]
公路弯道标志R=m表示圆弧道路所在圆的半径为m(米),某车在标有R=300处的弯道上从点A行驶了100π米到达点B(示意图如图7),则线段AB=
米.?
图7
8.[2020·枣庄]
如图8,AB是☉O的直径,PA切☉O于点A,线段PO交☉O于点C.连接BC.若∠P=36°,则∠B= .?
图8
9.[2020·湖州]
如图9,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .?
图9
10.[2020·株洲]
据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”.斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为正方形外接一个圆,此圆外是一个同心圆”,如图10所示.
问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为 尺.(结果用最简根式表示)?
图10
11.[2020·广元]
如图11,△ABC内接于☉O,AH⊥BC于点H.若AC=10,AH=8,☉O的半径为7,则AB= .?
图11
12.[2020·岳阳]
如图12,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是 .(写出所有正确结论的序号)?
①PB=PD;②的长为π;③∠DBE=45°;④△BCF∽△PFB;⑤CF·CP为定值.
图12
三、解答题
13.[2020·湘潭]
如图13,在△ABC中,AB=AC,以AB为直径的☉O交BC于点D,过点D作DE⊥AC,垂足为E.
(1)求证:△ABD≌△ACD;
(2)判断直线DE与☉O的位置关系,并说明理由.
图13
14.[2020·郴州]
如图14,△ABC内接于☉O,AB是☉O的直径.直线l与☉O相切于点A,在l上取一点D,使得DA=DC,线段DC,AB的延长线交于点E.
(1)求证:直线DC是☉O的切线;
(2)若BC=2,∠CAB=30°,求图中阴影部分的面积(结果保留π).
图14
15.[2020·株洲]
如图15,AB是☉O的直径,C是☉O上一点,连接AC,BC,直线MN过点C,满足∠BCM=∠BAC=α.
(1)求证:直线MN是☉O的切线;
(2)如图②,点D在线段BC上,过点D作DH⊥MN于点H,直线DH交☉O于点E,F,连接AF并延长交直线MN于点G,连接CE,且CE=.若☉O的半径为1,cosα=,求AG·ED的值.
图15
答案
1.[解析]
C ∵∠ACB=54°,
∴∠AOB=2∠ACB=108°.
∵OB=OA,
∴∠ABO=∠BAO=×(180°-∠AOB)=36°.
故选C.
2.[解析]
C ∵四边形ABCD是☉O的内接四边形,∠BCD=120°,
∴∠A=180°-∠BCD=60°,
由圆周角定理,得∠BOD=2∠A=120°.
故选C.
3.[解析]
D 如图,连接OB.
∵四边形OABC是菱形,
∴OA=AB.
∵OA=OB,
∴OA=AB=OB,
∴∠AOB=60°.
∵BD是☉O的切线,∴∠DBO=90°.
∵OB=1,∴BD=OB=.故选D.
4.[解析]
B A项,∵PA,PB为☉O的切线,
∴PA=PB,
∴△BPA是等腰三角形,故A项正确;
B项,由圆的对称性可知:AB⊥PD,但不一定平分PD,故B项不一定正确;
C项,连接OB,OA,如图.
∵PA,PB为☉O的切线,
∴∠OBP=∠OAP=90°,
∴点A,B都在以PO为直径的圆上,故C项正确;
D项,∵△BPA是等腰三角形,PD⊥AB,
∴PC为△BPA的边AB上的中线,故D项正确.
故选B.
5.[解析]
A 如图,连接BC,AC.
∵∠ADC和∠ABC所对的弧都是,
∴根据圆周角定理知,∠ADC=∠ABC.
在Rt△ACB中,根据锐角三角函数的定义知,
sin∠ABC=.
∵AC=2,BC=3,∴AB==,
∴sin∠ABC==,
∴sin∠ADC=.故选A.
6.B 7.300
8.[答案]
27°
[解析]
∵PA切☉O于点A,∴∠OAP=90°.
∵∠P=36°,∴∠AOP=54°,
∴∠B=∠AOP=27°.故答案为27°.
9.[答案]
3
[解析]
如图,过点O作OH⊥CD于点H,连接OC,则CH=DH=CD=4.
在Rt△OCH中,OH==3,
所以CD与AB之间的距离是3.
故答案为3.
10.[答案]
4
[解析]
如图.
∵四边形CDEF为正方形,
∴∠D=90°,CD=DE,
∴CE为正方形CDEF外接圆的直径,∠ECD=45°.
由题意,得AB=2.5,
∴CE=2.5-0.25×2=2,
∴CD=CE·cos∠ECD=2×=,
即正方形CDEF的周长为4尺.
故答案为4.
11.[答案]
[解析]
如图,作直径AD,连接BD.
∵AD为☉O的直径,
∴∠ABD=90°.
又AH⊥BC,
∴∠ABD=∠AHC.
由圆周角定理得∠D=∠C,
∴△ABD∽△AHC,
∴=,即=,
解得AB=.故答案为.
12.[答案]
②⑤
[解析]
①连接AC并延长,与BD的延长线交于点H,如图.
∵M,C是半圆O上的三等分点,
∴∠BAH=30°.
∵BD与半圆O相切于点B.
∴∠ABD=90°,∴∠H=60°.
∵∠ACP=∠ABP,∠ACP=∠DCH,
∴∠PDB=∠H+∠DCH=∠ABP+60°.
∵∠PBD=90°-∠ABP,
若∠PDB=∠PBD,则∠ABP+60°=90°-∠ABP,
∴∠ABP=15°,
∴P为的中点,这与P为上的一动点不完全吻合,
∴∠PDB不一定等于∠PBD,
∴PB不一定等于PD,故①错误;
②∵M,C是半圆O上的三等分点,
∴∠BOC=×180°=60°.
∵AB=8,∴OB=OC=4,
∴的长度==π,故②正确;
③∵∠BOC=60°,OB=OC,
∴∠ABC=60°,OB=OC=BC.
∵BE⊥OC,∴∠OBE=∠CBE=30°.
∵∠ABD=90°,∴∠DBE=60°,
故③错误;
④∵M,C是的三等分点,
∴∠BPC=30°.
∵∠CBF=30°,∴∠CBF=∠CPB.
∵∠BCF=∠PCB,∴△BCF∽△PCB,
故④错误;
⑤∵△BCF∽△PCB,
∴=,
∴CF·CP=CB2.
∵CB=OB=OC=AB=4,
∴CF·CP=16,故⑤正确.
故答案为②⑤.
13.解:(1)证明:∵AB为☉O的直径,
∴AD⊥BC.
在Rt△ABD和Rt△ACD中,∵AD=AD,
AB=AC,
∴Rt△ABD≌Rt△ACD(HL).
(2)直线DE与☉O相切.理由如下:
连接OD,如图所示.
由△ABD≌△ACD知BD=DC.
又∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE.
又∵OD为☉O的半径,
∴直线DE与☉O相切.
14.解:(1)证明:如图,连接OC.
∵AB是☉O的直径,直线l与☉O相切于点A,
∴∠DAB=90°.
∵DA=DC,OA=OC,
∴∠DAC=∠DCA,∠OAC=∠OCA,
∴∠DCA+∠ACO=∠DAC+∠CAO,
即∠DCO=∠DAO=90°,∴OC⊥CD.
又OC是☉O的半径,
∴直线DC是☉O的切线.
(2)∵∠CAB=30°,
∴∠BOC=2∠CAB=60°.
∵OC=OB,∴△COB是等边三角形,
∴OC=OB=BC=2,∴CE=OC=2,
∴图中阴影部分的面积=S△OCE-S扇形COB=×2×2-=2-.
15.解:(1)证明:连接OC,如图.
∵AB是☉O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°.
∵OC=OB,
∴∠B=∠OCB.
∵∠BCM=∠BAC,
∴∠OCB+∠BCM=90°,即OC⊥MN.
又∵OC是☉O的半径,
∴直线MN是☉O的切线.
(2)∵AB是☉O的直径,☉O的半径为1,
∴AB=2.
∵cos∠BAC=cosα==,即=,
∴AC=.
∵∠AFE=∠ACE,∠GFH=∠AFE,
∴∠GFH=∠ACE.
∵DH⊥MN,
∴∠GFH+∠AGC=90°.
∵∠ACE+∠ECD=90°,
∴∠ECD=∠AGC.
又∵∠DEC=∠CAG,
∴△EDC∽△ACG,
∴=,
∴AG·ED=AC·CE=×=.
中考演练
一、选择题
1.[2020·淮安]
如图1,点A,B,C在☉O上,∠ACB=54°,则∠ABO的度数是
( )
图1
A.54°
B.27°
C.36°
D.108°
2.[2020·张家界]
如图2,四边形ABCD为☉O的内接四边形,∠BCD=120°,则∠BOD的度数为
( )
图2
A.100°
B.110°
C.120°
D.130°
3.[2020·温州]
如图3,菱形OABC的顶点A,B,C都在☉O上,过点B作☉O的切线交OA的延长线于点D.若☉O的半径为1,则BD的长为
( )
图3
A.1
B.2
C.
D.
4.[2020·湘西州]
如图4,PA,PB为☉O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交☉O于点D.下列结论不一定成立的是
( )
图4
A.△BPA为等腰三角形
B.AB与PD互相垂直平分
C.点A,B都在以PO为直径的圆上
D.PC为△BPA的边AB上的中线
5.[2020·扬州]
如图5,由边长均为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin∠ADC的值为
( )
图5
A.
B.
C.
D.
6.[2020·黔东南州]
如图6,正方形ABCD的边长为2,O为对角线的交点,E,F分别为BC,AD的中点.以点C为圆心,2为半径作圆弧,再分别以点E,F为圆心,1为半径作圆弧,,则图中阴影部分的面积为
( )
图6
A.π-1
B.π-2
C.π-3
D.4-π
二、填空题
7.[2020·娄底改编]
公路弯道标志R=m表示圆弧道路所在圆的半径为m(米),某车在标有R=300处的弯道上从点A行驶了100π米到达点B(示意图如图7),则线段AB=
米.?
图7
8.[2020·枣庄]
如图8,AB是☉O的直径,PA切☉O于点A,线段PO交☉O于点C.连接BC.若∠P=36°,则∠B= .?
图8
9.[2020·湖州]
如图9,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .?
图9
10.[2020·株洲]
据《汉书律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也”.斛是中国古代的一种量器,“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为正方形外接一个圆,此圆外是一个同心圆”,如图10所示.
问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为 尺.(结果用最简根式表示)?
图10
11.[2020·广元]
如图11,△ABC内接于☉O,AH⊥BC于点H.若AC=10,AH=8,☉O的半径为7,则AB= .?
图11
12.[2020·岳阳]
如图12,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是 .(写出所有正确结论的序号)?
①PB=PD;②的长为π;③∠DBE=45°;④△BCF∽△PFB;⑤CF·CP为定值.
图12
三、解答题
13.[2020·湘潭]
如图13,在△ABC中,AB=AC,以AB为直径的☉O交BC于点D,过点D作DE⊥AC,垂足为E.
(1)求证:△ABD≌△ACD;
(2)判断直线DE与☉O的位置关系,并说明理由.
图13
14.[2020·郴州]
如图14,△ABC内接于☉O,AB是☉O的直径.直线l与☉O相切于点A,在l上取一点D,使得DA=DC,线段DC,AB的延长线交于点E.
(1)求证:直线DC是☉O的切线;
(2)若BC=2,∠CAB=30°,求图中阴影部分的面积(结果保留π).
图14
15.[2020·株洲]
如图15,AB是☉O的直径,C是☉O上一点,连接AC,BC,直线MN过点C,满足∠BCM=∠BAC=α.
(1)求证:直线MN是☉O的切线;
(2)如图②,点D在线段BC上,过点D作DH⊥MN于点H,直线DH交☉O于点E,F,连接AF并延长交直线MN于点G,连接CE,且CE=.若☉O的半径为1,cosα=,求AG·ED的值.
图15
答案
1.[解析]
C ∵∠ACB=54°,
∴∠AOB=2∠ACB=108°.
∵OB=OA,
∴∠ABO=∠BAO=×(180°-∠AOB)=36°.
故选C.
2.[解析]
C ∵四边形ABCD是☉O的内接四边形,∠BCD=120°,
∴∠A=180°-∠BCD=60°,
由圆周角定理,得∠BOD=2∠A=120°.
故选C.
3.[解析]
D 如图,连接OB.
∵四边形OABC是菱形,
∴OA=AB.
∵OA=OB,
∴OA=AB=OB,
∴∠AOB=60°.
∵BD是☉O的切线,∴∠DBO=90°.
∵OB=1,∴BD=OB=.故选D.
4.[解析]
B A项,∵PA,PB为☉O的切线,
∴PA=PB,
∴△BPA是等腰三角形,故A项正确;
B项,由圆的对称性可知:AB⊥PD,但不一定平分PD,故B项不一定正确;
C项,连接OB,OA,如图.
∵PA,PB为☉O的切线,
∴∠OBP=∠OAP=90°,
∴点A,B都在以PO为直径的圆上,故C项正确;
D项,∵△BPA是等腰三角形,PD⊥AB,
∴PC为△BPA的边AB上的中线,故D项正确.
故选B.
5.[解析]
A 如图,连接BC,AC.
∵∠ADC和∠ABC所对的弧都是,
∴根据圆周角定理知,∠ADC=∠ABC.
在Rt△ACB中,根据锐角三角函数的定义知,
sin∠ABC=.
∵AC=2,BC=3,∴AB==,
∴sin∠ABC==,
∴sin∠ADC=.故选A.
6.B 7.300
8.[答案]
27°
[解析]
∵PA切☉O于点A,∴∠OAP=90°.
∵∠P=36°,∴∠AOP=54°,
∴∠B=∠AOP=27°.故答案为27°.
9.[答案]
3
[解析]
如图,过点O作OH⊥CD于点H,连接OC,则CH=DH=CD=4.
在Rt△OCH中,OH==3,
所以CD与AB之间的距离是3.
故答案为3.
10.[答案]
4
[解析]
如图.
∵四边形CDEF为正方形,
∴∠D=90°,CD=DE,
∴CE为正方形CDEF外接圆的直径,∠ECD=45°.
由题意,得AB=2.5,
∴CE=2.5-0.25×2=2,
∴CD=CE·cos∠ECD=2×=,
即正方形CDEF的周长为4尺.
故答案为4.
11.[答案]
[解析]
如图,作直径AD,连接BD.
∵AD为☉O的直径,
∴∠ABD=90°.
又AH⊥BC,
∴∠ABD=∠AHC.
由圆周角定理得∠D=∠C,
∴△ABD∽△AHC,
∴=,即=,
解得AB=.故答案为.
12.[答案]
②⑤
[解析]
①连接AC并延长,与BD的延长线交于点H,如图.
∵M,C是半圆O上的三等分点,
∴∠BAH=30°.
∵BD与半圆O相切于点B.
∴∠ABD=90°,∴∠H=60°.
∵∠ACP=∠ABP,∠ACP=∠DCH,
∴∠PDB=∠H+∠DCH=∠ABP+60°.
∵∠PBD=90°-∠ABP,
若∠PDB=∠PBD,则∠ABP+60°=90°-∠ABP,
∴∠ABP=15°,
∴P为的中点,这与P为上的一动点不完全吻合,
∴∠PDB不一定等于∠PBD,
∴PB不一定等于PD,故①错误;
②∵M,C是半圆O上的三等分点,
∴∠BOC=×180°=60°.
∵AB=8,∴OB=OC=4,
∴的长度==π,故②正确;
③∵∠BOC=60°,OB=OC,
∴∠ABC=60°,OB=OC=BC.
∵BE⊥OC,∴∠OBE=∠CBE=30°.
∵∠ABD=90°,∴∠DBE=60°,
故③错误;
④∵M,C是的三等分点,
∴∠BPC=30°.
∵∠CBF=30°,∴∠CBF=∠CPB.
∵∠BCF=∠PCB,∴△BCF∽△PCB,
故④错误;
⑤∵△BCF∽△PCB,
∴=,
∴CF·CP=CB2.
∵CB=OB=OC=AB=4,
∴CF·CP=16,故⑤正确.
故答案为②⑤.
13.解:(1)证明:∵AB为☉O的直径,
∴AD⊥BC.
在Rt△ABD和Rt△ACD中,∵AD=AD,
AB=AC,
∴Rt△ABD≌Rt△ACD(HL).
(2)直线DE与☉O相切.理由如下:
连接OD,如图所示.
由△ABD≌△ACD知BD=DC.
又∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE.
又∵OD为☉O的半径,
∴直线DE与☉O相切.
14.解:(1)证明:如图,连接OC.
∵AB是☉O的直径,直线l与☉O相切于点A,
∴∠DAB=90°.
∵DA=DC,OA=OC,
∴∠DAC=∠DCA,∠OAC=∠OCA,
∴∠DCA+∠ACO=∠DAC+∠CAO,
即∠DCO=∠DAO=90°,∴OC⊥CD.
又OC是☉O的半径,
∴直线DC是☉O的切线.
(2)∵∠CAB=30°,
∴∠BOC=2∠CAB=60°.
∵OC=OB,∴△COB是等边三角形,
∴OC=OB=BC=2,∴CE=OC=2,
∴图中阴影部分的面积=S△OCE-S扇形COB=×2×2-=2-.
15.解:(1)证明:连接OC,如图.
∵AB是☉O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°.
∵OC=OB,
∴∠B=∠OCB.
∵∠BCM=∠BAC,
∴∠OCB+∠BCM=90°,即OC⊥MN.
又∵OC是☉O的半径,
∴直线MN是☉O的切线.
(2)∵AB是☉O的直径,☉O的半径为1,
∴AB=2.
∵cos∠BAC=cosα==,即=,
∴AC=.
∵∠AFE=∠ACE,∠GFH=∠AFE,
∴∠GFH=∠ACE.
∵DH⊥MN,
∴∠GFH+∠AGC=90°.
∵∠ACE+∠ECD=90°,
∴∠ECD=∠AGC.
又∵∠DEC=∠CAG,
∴△EDC∽△ACG,
∴=,
∴AG·ED=AC·CE=×=.
