沪科版(2012)初中数学八年级上册15.2 线段的垂直平分线的性质 课件(16张)
文档属性
| 名称 | 沪科版(2012)初中数学八年级上册15.2 线段的垂直平分线的性质 课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 612.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
《线段的垂直平分线的性质》
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
O
已知直线
l
和一个点A,如何画出点A关于
l
的对称点A′
?
A
A′
l
尝试探究
直线l就是对应点连线段A
A′的垂直平分线
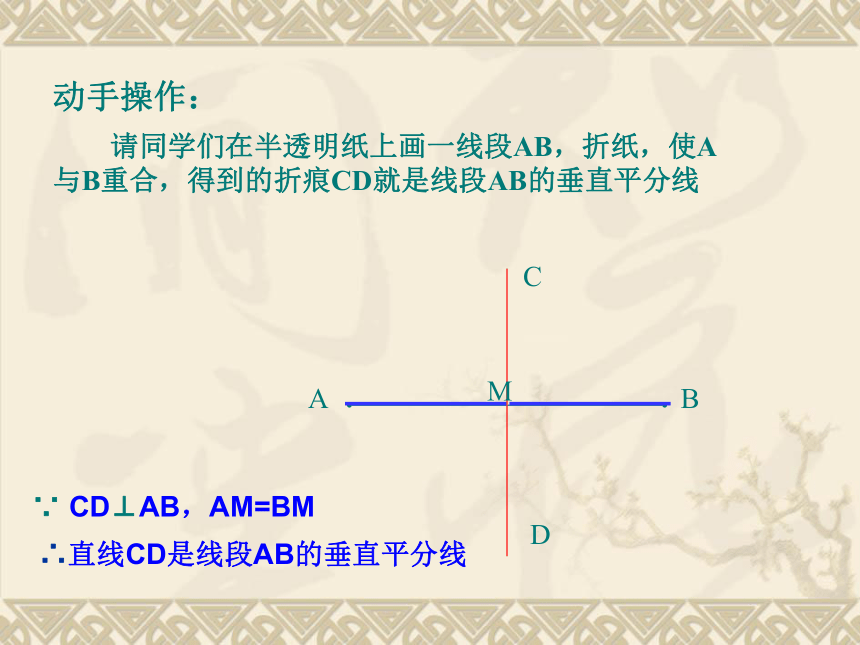
A
C
D
B
M
请同学们在半透明纸上画一线段AB,折纸,使A与B重合,得到的折痕CD就是线段AB的垂直平分线
动手操作:
∵
CD⊥AB,AM=BM
∴直线CD是线段AB的垂直平分线
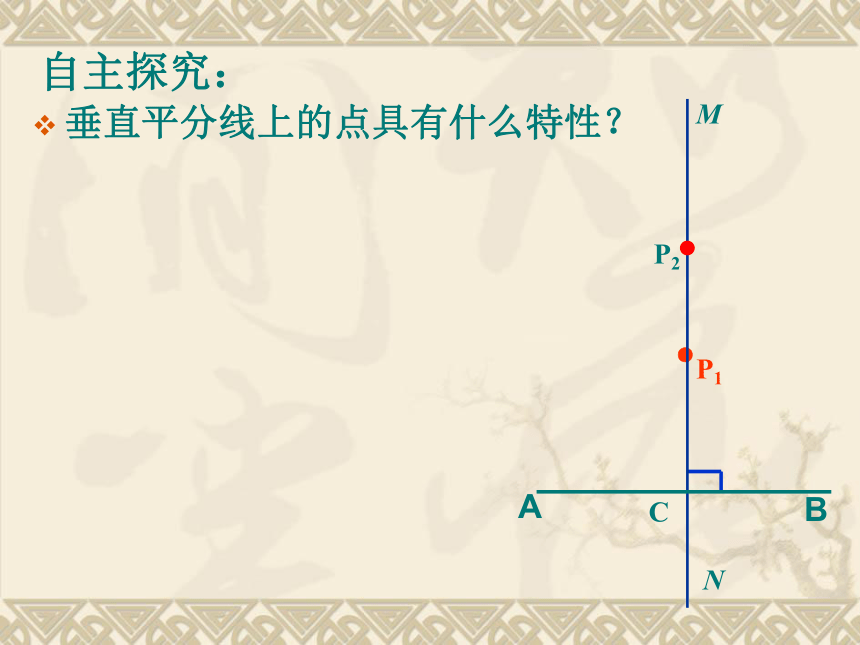
自主探究:
垂直平分线上的点具有什么特性?
P2
M
N
C
●
P1
A
B
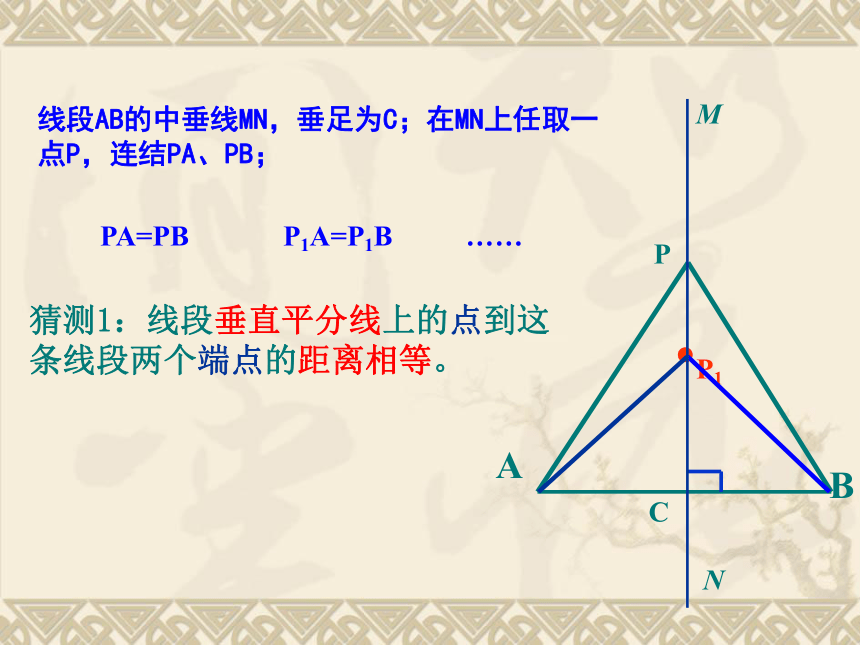
线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;
P
M
N
C
PA=PB
P1A=P1B
……
A
B
●
P1
猜测1:线段垂直平分线上的点到这条线段两个端点的距离相等。
性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
已知:如图,直线MN⊥线段AB,垂足为C,
且AC=CB.
求证:PA=PB
A
B
P
M
N
C
证明:∵ MN⊥AB
于点C
(已知),
∴
∠PCA=
∠PCB=90°(垂直的定义).
在
△PAC和△PBC中,
AC=BC(已知),
∠PCA=
∠PCB(已证),
PC=PC(公共边)
∴
△PAC
≌△
PBC(SAS).
∴PA=PB(全等三角形的对应边相等).
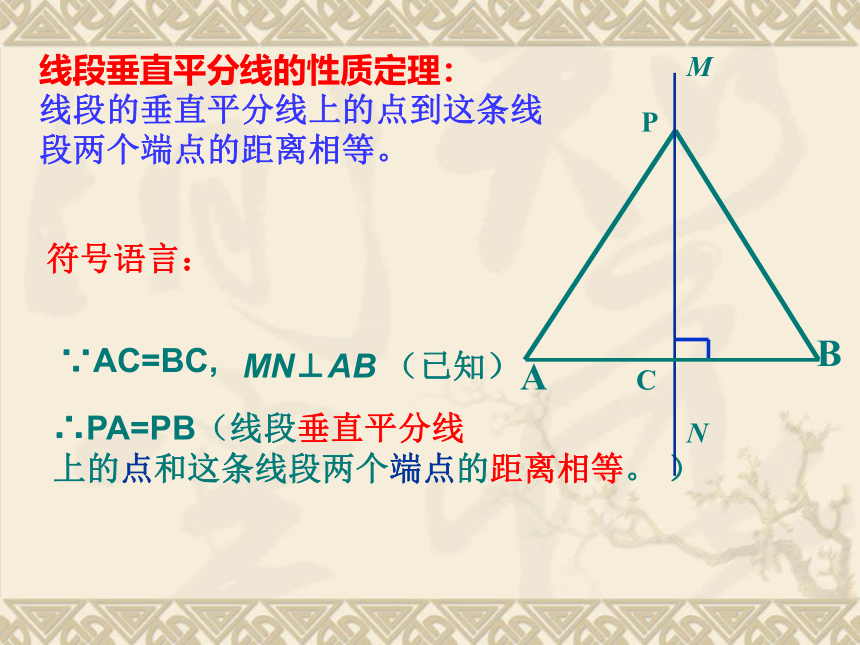
线段垂直平分线的性质定理:
线段的垂直平分线上的点到这条线段两个端点的距离相等。
∵AC=BC,
MN⊥AB
(已知)
∴PA=PB(线段垂直平分线
上的点和这条线段两个端点的距离相等。
)
符号语言:
P
M
N
C
A
B
1、如图线段MN被直线AB垂直平分,则ME=NE
√
课堂练习
判断题
A
B
M
N
E
2、如图直线MN垂直平分线段AB,则AE=AF
判断题
课堂练习
A
B
M
E
F
N
A
B
L
实际问题
在国道L的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得医院到两个工厂的距离相等,问医院的院址应选在何处?
104
国
道
线段的垂直平分线
如图,在直线l上求作一点P,使PA=PB.
实际问题
数学化
数学问题源于生活实践,反过来数学又为生活实践服务
A
B
l
P
综合提高:
已知:如图,直线l是线段AB的垂直平分线交AB于C点,D,E是l上的任意两点(除AB的中点外)
B
l
E
D
A
C
1、
EA=EB
2、
∠DAE=
∠DBE
4、
AD=AE
?
3、还有哪些线段和角是相等的?
小试牛刀:
例1、如图所示,在ΔABC中,边BC的垂直平分线MN分别交AB于点M,交BC于点N,
ΔBMC的周长为23,且BM=7,求BC的长。
C
B
M
N
A
解:∵
MN是线段BC的垂直平分线
BM=7
∴
CM=BM=7
∵
ΔBMC
的周长=23
∴BM+CM+BC=23
∴BC=23-CM-BM
=23-7-7
=9
课堂小结:
1、这节课你有什么收获?
2、当两条线段是垂直平分线上的线段两端点的距离时,淡化了用全等三角形的证明方法,可以运用今天学习的性质定理可以直接得到求解。
作业布置:
1、习题15.2
第1,2,3题
2、预习垂直平分线的判定定理
结束语
同学们,这节课到这里就结束了,
谢谢你们的参与!
《线段的垂直平分线的性质》
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
O
已知直线
l
和一个点A,如何画出点A关于
l
的对称点A′
?
A
A′
l
尝试探究
直线l就是对应点连线段A
A′的垂直平分线
A
C
D
B
M
请同学们在半透明纸上画一线段AB,折纸,使A与B重合,得到的折痕CD就是线段AB的垂直平分线
动手操作:
∵
CD⊥AB,AM=BM
∴直线CD是线段AB的垂直平分线
自主探究:
垂直平分线上的点具有什么特性?
P2
M
N
C
●
P1
A
B
线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;
P
M
N
C
PA=PB
P1A=P1B
……
A
B
●
P1
猜测1:线段垂直平分线上的点到这条线段两个端点的距离相等。
性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
已知:如图,直线MN⊥线段AB,垂足为C,
且AC=CB.
求证:PA=PB
A
B
P
M
N
C
证明:∵ MN⊥AB
于点C
(已知),
∴
∠PCA=
∠PCB=90°(垂直的定义).
在
△PAC和△PBC中,
AC=BC(已知),
∠PCA=
∠PCB(已证),
PC=PC(公共边)
∴
△PAC
≌△
PBC(SAS).
∴PA=PB(全等三角形的对应边相等).
线段垂直平分线的性质定理:
线段的垂直平分线上的点到这条线段两个端点的距离相等。
∵AC=BC,
MN⊥AB
(已知)
∴PA=PB(线段垂直平分线
上的点和这条线段两个端点的距离相等。
)
符号语言:
P
M
N
C
A
B
1、如图线段MN被直线AB垂直平分,则ME=NE
√
课堂练习
判断题
A
B
M
N
E
2、如图直线MN垂直平分线段AB,则AE=AF
判断题
课堂练习
A
B
M
E
F
N
A
B
L
实际问题
在国道L的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得医院到两个工厂的距离相等,问医院的院址应选在何处?
104
国
道
线段的垂直平分线
如图,在直线l上求作一点P,使PA=PB.
实际问题
数学化
数学问题源于生活实践,反过来数学又为生活实践服务
A
B
l
P
综合提高:
已知:如图,直线l是线段AB的垂直平分线交AB于C点,D,E是l上的任意两点(除AB的中点外)
B
l
E
D
A
C
1、
EA=EB
2、
∠DAE=
∠DBE
4、
AD=AE
?
3、还有哪些线段和角是相等的?
小试牛刀:
例1、如图所示,在ΔABC中,边BC的垂直平分线MN分别交AB于点M,交BC于点N,
ΔBMC的周长为23,且BM=7,求BC的长。
C
B
M
N
A
解:∵
MN是线段BC的垂直平分线
BM=7
∴
CM=BM=7
∵
ΔBMC
的周长=23
∴BM+CM+BC=23
∴BC=23-CM-BM
=23-7-7
=9
课堂小结:
1、这节课你有什么收获?
2、当两条线段是垂直平分线上的线段两端点的距离时,淡化了用全等三角形的证明方法,可以运用今天学习的性质定理可以直接得到求解。
作业布置:
1、习题15.2
第1,2,3题
2、预习垂直平分线的判定定理
结束语
同学们,这节课到这里就结束了,
谢谢你们的参与!
