人教版七年级数学下册 课件-8.4三元一次方程组的解法(25张)
文档属性
| 名称 | 人教版七年级数学下册 课件-8.4三元一次方程组的解法(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 21:48:39 | ||
图片预览







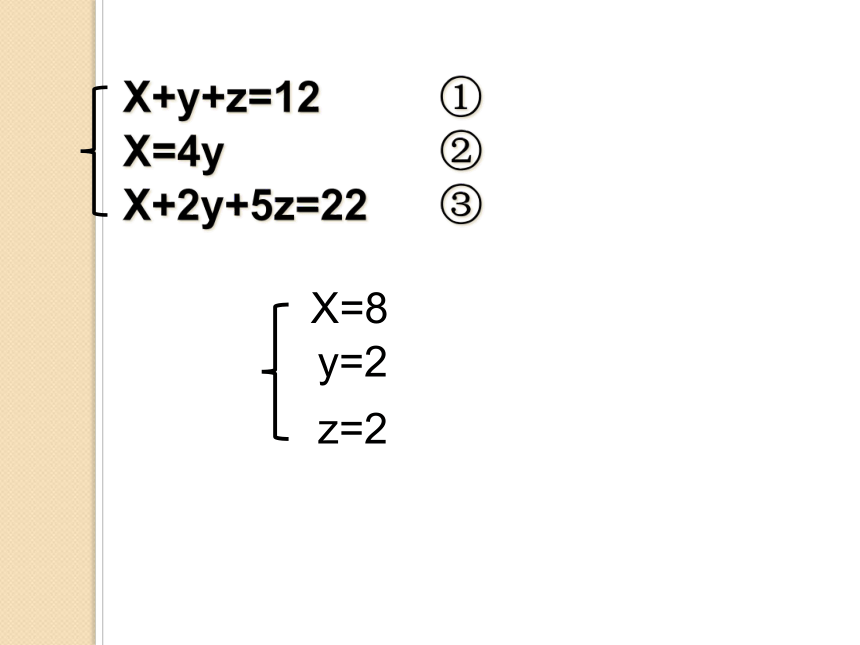
文档简介
(共25张PPT)
8.4
三元一次方程组
及其解法
解二元一次方程组有哪几种方法?它们的基本思想是什么?
二元一次方程组
代入
加减
消元
一元一次方程
什么叫做二元一次方程组?
方程组中含有两个未知数,且含未知数的项的次数是一次,这样的方程组叫做二元一次方程组。
复习导入
问题回顾
“我们的小世界杯”足球赛第二轮比赛中,勇士队参加了10场比赛,按同样的计分规则,共得18分。已知勇士队在比赛中胜的场数正好等于平与负的场数之和,那么勇士队在第二轮比赛中胜、平、负的场数各是多少?
这个问题中包含有
个未知数,有
个相等关系,分别是什么?
分析:
解:设勇士队在第二轮比赛中,胜、平、负的场数分别是x、y、z场,根据题意,有
X+y+z=10
①
3x+y=18
②
X=y+z
③
解:设勇士队在第二轮比赛中,胜、平、负的场数分别是x、y、z场,根据题意,有
3x+y=18
②
X+y+z=10
①
X=y+z
③
观察方程
问题:1、什么叫三元一次方程?
2、什么叫三元一次方程组?
2、含有三个未知数,每个方程中含未知数的项的次数都是1,像这样的方程组叫做三元一次方程组。
1、都含有三个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做三元一次方程。
X+y+z=10
①
3x+y=18
②
X=y+z
③
解:设勇士队在第二轮比赛中,胜、平、负的场数分别是x、y、z场,根据题意,有
把③代入①、
②
,得
2y+2z=10
④
4y+3z=18
⑤
解之得
y=3
z=2
把y=3,z=2代入方程③,得
X=5
∴
X=5
y=3
z=2
相信自己
小明手头有12张面额分别为1元、2元、5元的
纸币,共计22元,其中1元的纸币的张数是2
元
纸币张数的4倍.求1元、2元、5元纸币各多少
张?
分析:
这个问题中包含有
个相等关系:
1元纸币张数+2元纸币张数+5元纸币张数=12张
1元纸币的张数=2元纸币的张数的4倍
1元的金额+2元的金额+5元的金额=22元
试一试
设1元、2元、5元的纸币分别为x张、y张、z张
根据题意,可以得到下面三个方程:
X+y+z=12
X=4y
X+2y+5z=22
①
②
③
X+2y+5z=22
③
X+y+z=12
①
X=4y
②
X=8
y=2
z=2
三元一次方程组
一元一次方程
二元一次方程组
1.化“三元”为“二元”
总结
消元
消元
三元一次方程组求法步骤:
2.化“二元”为“一元”
怎样解三元一次方程组?
(也就是消去一个未知数)
问题1
解方程组
x-z=4.
③
1
.
化“三元”为“二元”
考虑消去哪个未知数(也就是三个未知数要去掉哪一个?)
2.
化“二元”为“一元”
。
x-y+z=
0
②
x+y+z=
2
①
交流探究
解: ①+②,得
2x+2z=2
,
化简,得
x+z=1
④
③+④,得
2x=5
,
y=1
注:如果三个方程中有一个方程是二元一次方程(如例1中的③),则可以先通过对另外两个方程组进行消元,消元时就消去三个元中这个二元一次方程(如例1中的③)中缺少的那个元。缺某元,消某元。
①
③
②
在三元化二元时,对于具体方法的选取应该注意选择最恰当、最简便的方法。
分析:方程①中只含x,z,因此,可以由②③消去y,得到一个只含x,z的方程,与方程①组成一个二元一次方程组
解三元一次方程组
3x+4z=7
①
2x+3y+z=9
②
5x-9y+7z=8
③
{
解:②×3+③
,得
11x+10z=35
④
①与④组成方程组
3x+4z=7
11x+10z=35
{
解这个方程组,得
X=5
Z=-2
{
把x=5,z=-2代入②,得y=
因此,三元一次方程组的解为
X=5
Y=
Z=-2
{
①
②
③
练习:解方程组
思考:三元一次方程组降为二元一次方程组,说说消去哪个求知数,并说明理由!
解:
①
+③
得:
5x+5y=25
④
②+③
×2得:5x+7y=31
⑤
{
5x+5y=25
④
5x+7y=31
⑤
X=2
y=3
{
解得
把x=2,y=3代入②,得z=1
所以方程组的解为
x=2
y=3
z=1
{
解方程组
x+2y-3z=1
③
2x-3y+4z=3
①
3x-2y+z=7
②
解:
由方程②,得
Z=7-3x+2y
④
将④分别代入方程①和③
,得
2x-3y+4(7-3x+2y)=3
X+2y-3(7-3x+2y)=1
整理,得
-2x+y=-5
5x-2y=11
解这个二元一次方程组,得
X=1
Y=-3
代入④得
Z=-2
∴
X=1
y=-3
z=-2
解方程组
x+2y-3z=1
③
2x-3y+4z=3
①
3x-2y+z=7
②
解:
①
-③
×
2,得
-7y+10z=1
④
②
-③
×3
,得
-8y+10z=4
⑤
④-
⑤得
y=-3
把y=-3代入④得
把y=-3,z=-2代入①得
X=1
∴
X=1
y=-3
z=-2
Z=-2
分析:三个方程中未知数的系数都不是1或-1,用代入消元法比较麻烦,可考虑用加减消元法求解。
问题3:解方程组
解:
③
-
②,得
3x+6z=-24
即
x+2z=-8
④
①
×3+
②
×4,得
17x-17z=17
即
x-z=1
⑤
联立④,⑤,得
解得
将x=-2,z=-3代入方程②,得y=0.
所以原方程组的解是
x+y-z=6
x-3y+2z=1
3x+2y-z=4
解三元一次方程组
①
②
③
【答案】
4x+8y+5z=300
x+y+2z=67
x+y+z=51
x=15
y=20
解得:
z=16
己知
,求
的值。
练习:
在等式
y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60.
求a,b,c的值
解:根据题意,得三元一次方程组
a-b+c=
0
①
4a+2b+c=3
②
25a+5b+c=60
③
②-①,
得
a+b=1
④
③-①,得
4a+b=10
⑤
④与⑤组成二元一次方程组
a+b=1
4a+b=10
a=3
b=-2
解这个方程组,得
把
代入①,得
a=3
b=-2
{
c=-5
a=3
b=-2
c=-5
因此
答:a=3,
b=-2,
c=-5.
一元一次方程
求出第一个未知数的值
求出第三个未知数的值
求出第二个未知数的值
二元一次方程组
三元一次方程组
消元
消元
8.4
三元一次方程组
及其解法
解二元一次方程组有哪几种方法?它们的基本思想是什么?
二元一次方程组
代入
加减
消元
一元一次方程
什么叫做二元一次方程组?
方程组中含有两个未知数,且含未知数的项的次数是一次,这样的方程组叫做二元一次方程组。
复习导入
问题回顾
“我们的小世界杯”足球赛第二轮比赛中,勇士队参加了10场比赛,按同样的计分规则,共得18分。已知勇士队在比赛中胜的场数正好等于平与负的场数之和,那么勇士队在第二轮比赛中胜、平、负的场数各是多少?
这个问题中包含有
个未知数,有
个相等关系,分别是什么?
分析:
解:设勇士队在第二轮比赛中,胜、平、负的场数分别是x、y、z场,根据题意,有
X+y+z=10
①
3x+y=18
②
X=y+z
③
解:设勇士队在第二轮比赛中,胜、平、负的场数分别是x、y、z场,根据题意,有
3x+y=18
②
X+y+z=10
①
X=y+z
③
观察方程
问题:1、什么叫三元一次方程?
2、什么叫三元一次方程组?
2、含有三个未知数,每个方程中含未知数的项的次数都是1,像这样的方程组叫做三元一次方程组。
1、都含有三个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做三元一次方程。
X+y+z=10
①
3x+y=18
②
X=y+z
③
解:设勇士队在第二轮比赛中,胜、平、负的场数分别是x、y、z场,根据题意,有
把③代入①、
②
,得
2y+2z=10
④
4y+3z=18
⑤
解之得
y=3
z=2
把y=3,z=2代入方程③,得
X=5
∴
X=5
y=3
z=2
相信自己
小明手头有12张面额分别为1元、2元、5元的
纸币,共计22元,其中1元的纸币的张数是2
元
纸币张数的4倍.求1元、2元、5元纸币各多少
张?
分析:
这个问题中包含有
个相等关系:
1元纸币张数+2元纸币张数+5元纸币张数=12张
1元纸币的张数=2元纸币的张数的4倍
1元的金额+2元的金额+5元的金额=22元
试一试
设1元、2元、5元的纸币分别为x张、y张、z张
根据题意,可以得到下面三个方程:
X+y+z=12
X=4y
X+2y+5z=22
①
②
③
X+2y+5z=22
③
X+y+z=12
①
X=4y
②
X=8
y=2
z=2
三元一次方程组
一元一次方程
二元一次方程组
1.化“三元”为“二元”
总结
消元
消元
三元一次方程组求法步骤:
2.化“二元”为“一元”
怎样解三元一次方程组?
(也就是消去一个未知数)
问题1
解方程组
x-z=4.
③
1
.
化“三元”为“二元”
考虑消去哪个未知数(也就是三个未知数要去掉哪一个?)
2.
化“二元”为“一元”
。
x-y+z=
0
②
x+y+z=
2
①
交流探究
解: ①+②,得
2x+2z=2
,
化简,得
x+z=1
④
③+④,得
2x=5
,
y=1
注:如果三个方程中有一个方程是二元一次方程(如例1中的③),则可以先通过对另外两个方程组进行消元,消元时就消去三个元中这个二元一次方程(如例1中的③)中缺少的那个元。缺某元,消某元。
①
③
②
在三元化二元时,对于具体方法的选取应该注意选择最恰当、最简便的方法。
分析:方程①中只含x,z,因此,可以由②③消去y,得到一个只含x,z的方程,与方程①组成一个二元一次方程组
解三元一次方程组
3x+4z=7
①
2x+3y+z=9
②
5x-9y+7z=8
③
{
解:②×3+③
,得
11x+10z=35
④
①与④组成方程组
3x+4z=7
11x+10z=35
{
解这个方程组,得
X=5
Z=-2
{
把x=5,z=-2代入②,得y=
因此,三元一次方程组的解为
X=5
Y=
Z=-2
{
①
②
③
练习:解方程组
思考:三元一次方程组降为二元一次方程组,说说消去哪个求知数,并说明理由!
解:
①
+③
得:
5x+5y=25
④
②+③
×2得:5x+7y=31
⑤
{
5x+5y=25
④
5x+7y=31
⑤
X=2
y=3
{
解得
把x=2,y=3代入②,得z=1
所以方程组的解为
x=2
y=3
z=1
{
解方程组
x+2y-3z=1
③
2x-3y+4z=3
①
3x-2y+z=7
②
解:
由方程②,得
Z=7-3x+2y
④
将④分别代入方程①和③
,得
2x-3y+4(7-3x+2y)=3
X+2y-3(7-3x+2y)=1
整理,得
-2x+y=-5
5x-2y=11
解这个二元一次方程组,得
X=1
Y=-3
代入④得
Z=-2
∴
X=1
y=-3
z=-2
解方程组
x+2y-3z=1
③
2x-3y+4z=3
①
3x-2y+z=7
②
解:
①
-③
×
2,得
-7y+10z=1
④
②
-③
×3
,得
-8y+10z=4
⑤
④-
⑤得
y=-3
把y=-3代入④得
把y=-3,z=-2代入①得
X=1
∴
X=1
y=-3
z=-2
Z=-2
分析:三个方程中未知数的系数都不是1或-1,用代入消元法比较麻烦,可考虑用加减消元法求解。
问题3:解方程组
解:
③
-
②,得
3x+6z=-24
即
x+2z=-8
④
①
×3+
②
×4,得
17x-17z=17
即
x-z=1
⑤
联立④,⑤,得
解得
将x=-2,z=-3代入方程②,得y=0.
所以原方程组的解是
x+y-z=6
x-3y+2z=1
3x+2y-z=4
解三元一次方程组
①
②
③
【答案】
4x+8y+5z=300
x+y+2z=67
x+y+z=51
x=15
y=20
解得:
z=16
己知
,求
的值。
练习:
在等式
y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60.
求a,b,c的值
解:根据题意,得三元一次方程组
a-b+c=
0
①
4a+2b+c=3
②
25a+5b+c=60
③
②-①,
得
a+b=1
④
③-①,得
4a+b=10
⑤
④与⑤组成二元一次方程组
a+b=1
4a+b=10
a=3
b=-2
解这个方程组,得
把
代入①,得
a=3
b=-2
{
c=-5
a=3
b=-2
c=-5
因此
答:a=3,
b=-2,
c=-5.
一元一次方程
求出第一个未知数的值
求出第三个未知数的值
求出第二个未知数的值
二元一次方程组
三元一次方程组
消元
消元
