7.2.2定义与命题-北师大版八年级数学上册课件(17张)
文档属性
| 名称 | 7.2.2定义与命题-北师大版八年级数学上册课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 284.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
复习旧知(2分钟)
下列语句中,哪些是命题?哪些不是命题?如果是命题,判断其真假。
(1)作业做完了吗?
(2)对顶角相等.
(3)相等的角是对顶角.
不是命题
真命题
假命题
举一个反例就可以说明一个命题是假命题,
如何证实一个命题是真命题呢?
如何证明一个命题是真命题呢
用我们以前学过的观察,实验,特殊值等方法.
这些方法往往并不可靠.
哪些是已经知道的真命题呢?.
能不能根据已经知道的真命题证明呢?
哦……那可
怎么办
§7.2
定义与命题(2)
第七章 平行线的证明
1、
了解公理、证明、定理的概念,并熟记
本书所选用的公理。
2、会证明一个命题是真命题。
学习目标(1分钟)
证实其它命
题的正确性
推
理
2、公理:
1、原名:
3、证明:
4、定理:
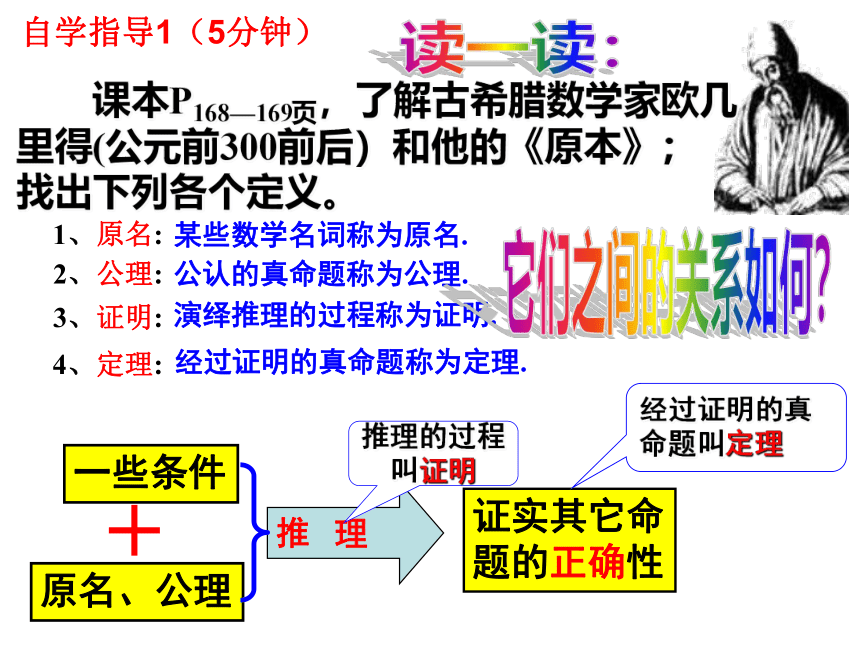
课本P168—169页,了解古希腊数学家欧几里得(公元前300前后)和他的《原本》;
找出下列各个定义。
某些数学名词称为原名.
公认的真命题称为公理.
演绎推理的过程称为证明.
经过证明的真命题称为定理.
推理的过程叫证明
经过证明的真命题叫定理
原名、公理
一些条件
+
读一读:
它们之间的关系如何?
自学指导1(5分钟)
1.两点确定一条直线。
2.两点之间,线段最短。
3.同一平面内,过一点有且只有一条直线与已知直线垂直。
4.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
5.过直线外一点有且只有一条直线与这条直线平行。
6.两边及其夹角对应相等的两个三角形全等。
7.两角及其夹边对应相等的两个三角形全等。
8.三边对应相等的两个三角形全等。
9.两条直线被一组平行线所截,所得的对应线段成比例(九年级学习)。
本套教材选用那几条基本事实作为证明的公理?
读一读:
(简述为:同位角相等,两直线平行)
(SAS)
(ASA)
(SSS)
本套教材选用如下九条基本事实作为证明的公理
等式和不等式的有关性质都可以看作公理
在等式中,一个量可以用它相等的量来代替.
其它哪些还可以作为公理?
数与式的运算律和运算法则都可以看作公理
例如:如果
a=b
,
b=c
,那么
a=c
,
这一性质也可看作公理,称为“等量代换”.
又如:如果
a>b
,
b>c
,那么
a>c
,
这一性质也可看作公理。
“不等式的传递性”
1、“两点之间,线段最短”这个语句是(
)
A、定理
B、公理
C、定义
D、不是命题
自学检测1(6分钟)
B
2、判断下列说法的正误。
(1)所有定理都不是命题(
)
(2)所有定理都是命题
(
)
(3)所有公理都是命题
(
)
(4)所有命题都是定理
(
)
√
√
×
×
3.下列句子中,是定理的是(
),是公理的是(
),
是定义的是(
)
A、若a=b,b=c,则a=c;
B、对顶角相等
C、三边分别相等的两个三角形全等。
D、形如 的式子叫做二次根式。
A
B
D
等量代换
C
从这些公理出发,就可以证明已经探索过的结论了。例如,我们可以证明下面的定理;
定理
同角(等角)的补角相等
定理
同角(等角)的余角相等
定理
三角形的任意两边之和大于第三边
定理
对顶角相等
自学指导2(5分钟)
如图,直线AB、CD相
交于点O,
∠1和∠2是对顶角,
证明:∵
∠1+∠AOC=180
°( )
∠2+∠AOC=180
°(
)
∴
∠1=
∠2( )
∠1=
∠2。
求证:
已知:
讨论:证明命题“对顶角相等”是真命题”
有哪些步骤?
1平角=180
°
1平角=180
°
同角的补角相等
A
C
B
D
O
)1
)
2
画图
写已知
证明
1、根据条件画图、写已知
2、根据结论写求证
3、根据已知条件及图写出证明过程
写求证
证明:同角的补角相等。
证明:
A
C
B
D
O
)1
)
2
如图,直线AB、CD相交于点O,
∠1是∠AOC的补角,
∠2是∠AOC的补角
∠1=
∠2
求证:
∵
∠1是∠AOC的补角
∴∠1+∠AOC=180
°
同理
∠2+∠AOC=180
°
∠2=180
°-∠AOC
∴∠1=180°-∠AOC
∴∠1=∠2
(补角的定义)
(等式的性质)
(等量代换)
自学检测2(5分钟)
别用自己证明自己哦!
证明:∵∠1与∠2是对顶角∴∠1=∠2
1、公理、证明、定理的概念及它们关系
推
理
演绎推理的过程叫证明
经过证明的真命题叫定理
证实其它命
题的正确性
原名、公理
一些条件
+
数学名词称为原名
公认的真命题称为公理
这节课你有什么收获?
小结(2分钟)
1、根据条件画图、写已知
2、根据结论写求证
3、根据已知条件及图写出证明过程
2、证明一个命题是真命题的步骤
易错点
难点
1、“同一平面内,不相交的两条直线叫做平行线”
这个语句是(
)
A定理
B公理
C定义
D只是命题
C
当堂训练(15分钟)
2、修建公路时,有时需将弯曲的公路改直,根据什么公理可以说明这样做能缩短路程(
)
A.直线
B.
两点确定一条直线
C.两点之间线段最短
D.平行
C
3、下列句子中,是定理的是(
),
是公理的是(
),是定义的(
)
A、同位角相等,两直线平行
B、两点确定一条直线
C、无限不循环小数叫做无理数
D、两直线平行,同位角相等
D
A
B
C
平行的判定公理
平行的性质定理
已知:
△
ABC
求证:AB+AC>BC
AB+BC>AC
AC+BC>AB
4、求证:“三角形任意两边之和大于第三边”。
A
B
C
证明:∵BC是以点B,点C为端点的线段,
∴AB+AC>BC( )
几何语言
图形语言
学习数学要培养自己的“转化思想”
文字语言
两点之间线段最短
同理:AB+AC>BC;
AC+BC>AB
∵
∠AOB+
∠BOC=900(已知)
∴∠AOB=
900
-∠BOC(等式的性质)
∵
∠
BOC+
∠COD=900 (已知)
∴∠COD=
900
-∠B
OC(等式的性质)
∴∠AOB=
∠COD(等量代换)
已知:如图∠AOC=900,
∠BOD=900
求证:
∠AOB=
∠COD
D
1、证明:同角的余角相等。
证明:如图
A
B
C
)
O
拔尖自助餐
∵
∠1+
∠B=900 (已知)
∴∠1=
900
-∠B(等式的性质)
∵
∠
A+
∠B=900 (已知)
∴∠A=
900
-∠B
(等式的性质)
∴∠1=
∠A(等量代换)
已知:如图∠1+
∠B=900
∠
A+
∠B=900
求证:
∠1=
∠A
A
B
C
D
)
1
1、证明:同角的余角相等。
证明:
2、下列命题是否正确?如正确加以证明,如不正确举出反例。
(1)代数式2x-x2-4的值一定是一个负数。
(2)对于分式
中x,y同时扩大为原来的2倍,那么分式的值不变。
7.2定义与命题(二)
板书设计
1、什么是公理?
2、什么是证明?
3、什么是定理?
4、证明命题的一般步骤。
公认的真命题是公理
演绎推理的过程叫证明
经过证明的真命题
1、根据条件画图、写已知
2、根据结论写求证
3、根据已知条件及图写出证明过程
复习旧知(2分钟)
下列语句中,哪些是命题?哪些不是命题?如果是命题,判断其真假。
(1)作业做完了吗?
(2)对顶角相等.
(3)相等的角是对顶角.
不是命题
真命题
假命题
举一个反例就可以说明一个命题是假命题,
如何证实一个命题是真命题呢?
如何证明一个命题是真命题呢
用我们以前学过的观察,实验,特殊值等方法.
这些方法往往并不可靠.
哪些是已经知道的真命题呢?.
能不能根据已经知道的真命题证明呢?
哦……那可
怎么办
§7.2
定义与命题(2)
第七章 平行线的证明
1、
了解公理、证明、定理的概念,并熟记
本书所选用的公理。
2、会证明一个命题是真命题。
学习目标(1分钟)
证实其它命
题的正确性
推
理
2、公理:
1、原名:
3、证明:
4、定理:
课本P168—169页,了解古希腊数学家欧几里得(公元前300前后)和他的《原本》;
找出下列各个定义。
某些数学名词称为原名.
公认的真命题称为公理.
演绎推理的过程称为证明.
经过证明的真命题称为定理.
推理的过程叫证明
经过证明的真命题叫定理
原名、公理
一些条件
+
读一读:
它们之间的关系如何?
自学指导1(5分钟)
1.两点确定一条直线。
2.两点之间,线段最短。
3.同一平面内,过一点有且只有一条直线与已知直线垂直。
4.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
5.过直线外一点有且只有一条直线与这条直线平行。
6.两边及其夹角对应相等的两个三角形全等。
7.两角及其夹边对应相等的两个三角形全等。
8.三边对应相等的两个三角形全等。
9.两条直线被一组平行线所截,所得的对应线段成比例(九年级学习)。
本套教材选用那几条基本事实作为证明的公理?
读一读:
(简述为:同位角相等,两直线平行)
(SAS)
(ASA)
(SSS)
本套教材选用如下九条基本事实作为证明的公理
等式和不等式的有关性质都可以看作公理
在等式中,一个量可以用它相等的量来代替.
其它哪些还可以作为公理?
数与式的运算律和运算法则都可以看作公理
例如:如果
a=b
,
b=c
,那么
a=c
,
这一性质也可看作公理,称为“等量代换”.
又如:如果
a>b
,
b>c
,那么
a>c
,
这一性质也可看作公理。
“不等式的传递性”
1、“两点之间,线段最短”这个语句是(
)
A、定理
B、公理
C、定义
D、不是命题
自学检测1(6分钟)
B
2、判断下列说法的正误。
(1)所有定理都不是命题(
)
(2)所有定理都是命题
(
)
(3)所有公理都是命题
(
)
(4)所有命题都是定理
(
)
√
√
×
×
3.下列句子中,是定理的是(
),是公理的是(
),
是定义的是(
)
A、若a=b,b=c,则a=c;
B、对顶角相等
C、三边分别相等的两个三角形全等。
D、形如 的式子叫做二次根式。
A
B
D
等量代换
C
从这些公理出发,就可以证明已经探索过的结论了。例如,我们可以证明下面的定理;
定理
同角(等角)的补角相等
定理
同角(等角)的余角相等
定理
三角形的任意两边之和大于第三边
定理
对顶角相等
自学指导2(5分钟)
如图,直线AB、CD相
交于点O,
∠1和∠2是对顶角,
证明:∵
∠1+∠AOC=180
°( )
∠2+∠AOC=180
°(
)
∴
∠1=
∠2( )
∠1=
∠2。
求证:
已知:
讨论:证明命题“对顶角相等”是真命题”
有哪些步骤?
1平角=180
°
1平角=180
°
同角的补角相等
A
C
B
D
O
)1
)
2
画图
写已知
证明
1、根据条件画图、写已知
2、根据结论写求证
3、根据已知条件及图写出证明过程
写求证
证明:同角的补角相等。
证明:
A
C
B
D
O
)1
)
2
如图,直线AB、CD相交于点O,
∠1是∠AOC的补角,
∠2是∠AOC的补角
∠1=
∠2
求证:
∵
∠1是∠AOC的补角
∴∠1+∠AOC=180
°
同理
∠2+∠AOC=180
°
∠2=180
°-∠AOC
∴∠1=180°-∠AOC
∴∠1=∠2
(补角的定义)
(等式的性质)
(等量代换)
自学检测2(5分钟)
别用自己证明自己哦!
证明:∵∠1与∠2是对顶角∴∠1=∠2
1、公理、证明、定理的概念及它们关系
推
理
演绎推理的过程叫证明
经过证明的真命题叫定理
证实其它命
题的正确性
原名、公理
一些条件
+
数学名词称为原名
公认的真命题称为公理
这节课你有什么收获?
小结(2分钟)
1、根据条件画图、写已知
2、根据结论写求证
3、根据已知条件及图写出证明过程
2、证明一个命题是真命题的步骤
易错点
难点
1、“同一平面内,不相交的两条直线叫做平行线”
这个语句是(
)
A定理
B公理
C定义
D只是命题
C
当堂训练(15分钟)
2、修建公路时,有时需将弯曲的公路改直,根据什么公理可以说明这样做能缩短路程(
)
A.直线
B.
两点确定一条直线
C.两点之间线段最短
D.平行
C
3、下列句子中,是定理的是(
),
是公理的是(
),是定义的(
)
A、同位角相等,两直线平行
B、两点确定一条直线
C、无限不循环小数叫做无理数
D、两直线平行,同位角相等
D
A
B
C
平行的判定公理
平行的性质定理
已知:
△
ABC
求证:AB+AC>BC
AB+BC>AC
AC+BC>AB
4、求证:“三角形任意两边之和大于第三边”。
A
B
C
证明:∵BC是以点B,点C为端点的线段,
∴AB+AC>BC( )
几何语言
图形语言
学习数学要培养自己的“转化思想”
文字语言
两点之间线段最短
同理:AB+AC>BC;
AC+BC>AB
∵
∠AOB+
∠BOC=900(已知)
∴∠AOB=
900
-∠BOC(等式的性质)
∵
∠
BOC+
∠COD=900 (已知)
∴∠COD=
900
-∠B
OC(等式的性质)
∴∠AOB=
∠COD(等量代换)
已知:如图∠AOC=900,
∠BOD=900
求证:
∠AOB=
∠COD
D
1、证明:同角的余角相等。
证明:如图
A
B
C
)
O
拔尖自助餐
∵
∠1+
∠B=900 (已知)
∴∠1=
900
-∠B(等式的性质)
∵
∠
A+
∠B=900 (已知)
∴∠A=
900
-∠B
(等式的性质)
∴∠1=
∠A(等量代换)
已知:如图∠1+
∠B=900
∠
A+
∠B=900
求证:
∠1=
∠A
A
B
C
D
)
1
1、证明:同角的余角相等。
证明:
2、下列命题是否正确?如正确加以证明,如不正确举出反例。
(1)代数式2x-x2-4的值一定是一个负数。
(2)对于分式
中x,y同时扩大为原来的2倍,那么分式的值不变。
7.2定义与命题(二)
板书设计
1、什么是公理?
2、什么是证明?
3、什么是定理?
4、证明命题的一般步骤。
公认的真命题是公理
演绎推理的过程叫证明
经过证明的真命题
1、根据条件画图、写已知
2、根据结论写求证
3、根据已知条件及图写出证明过程
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
