人教版七年级上册3.4实际问题与一元一次方程工程问题课件(14张)
文档属性
| 名称 | 人教版七年级上册3.4实际问题与一元一次方程工程问题课件(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 22:09:48 | ||
图片预览






文档简介
(共14张PPT)
3.4实际问题与一元一次方程
工程问题
学
科网
工程问题中的量及其关系:
1.工作效率:
2.工程问题中的基本关系:
工作量=
3.总工作量可看做“1”
4.合效率:各效率之和;
各部分工作量之和=工作总量
活动1.自主学习
难点强调
工作效率×工作时间
单位时间完成的工作量
知识回顾
?比一比,赛一赛.
看谁做得好,看谁做得快!
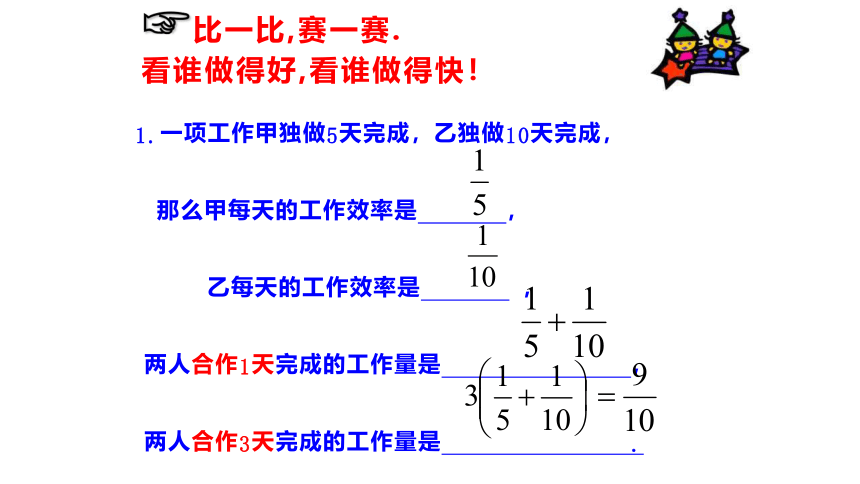
1.一项工作甲独做5天完成,乙独做10天完成,
那么甲每天的工作效率是
,
乙每天的工作效率是
,
两人合作1天完成的工作量是
,
两人合作3天完成的工作量是
.
一件工作,甲单独做x小时完成,乙单
独做y小时完成,那么甲、乙的工作效率分
别为???
????、????
???;甲、乙合作m天可以完成
的工作量为???
?
或
???。
引例:
请同学们模仿例1的分析思路,完成例2的题目分析解答.
例1
整理一批图书,由一个人做要40
h完成.现在计划由一部分人先做4
h,再增加
2人和他们一起做8
h,完成这项工作.假设这些人的工作效率相同,具体应安排多少人工作?
总工作量
每个人的工作效率
先安排的人数
增加的人数
先安排的人的工作时间
增加的人的工作时间
先安排的人完成的工作量
增加的人完成的工作量
(1)请你一边阅读题目,一边画出文段中的关键信息,并用自己的语言概括出来.
(2)设适当的未知数,将上述问题在表格中表示出来.
1
x人
2人
(4+8)小时
(3)总的工作量如何表示呢?
8小时
两批人完成的工作量之和
解:设安排
x人先做4
h,根据题意可得
解方程得
x=2.
答:应安排2人先做4
h.
例2、某管道由甲、乙两工程队单独施工分别需要30
天、20天。
(1)如果两队从两端同时相向施工,需要多少
天铺好?
(2)又知甲队单独施工每天需付200元的施工
费,乙队单独施工每天需付280元施工费,
那么是由甲队单独施工,还是乙队单独施
工,还是两队同时施工,请你按照少花钱
多办事的原则,设计一个方案,并说明理
由。
巩固练习
解:(1)设需要
x
天铺好,依题意,得:
解得:
x
=
12
∴
需要12天铺好。
(2)若单独由甲队施工,则需30天完成,花费
200×30=6000(元);
若单独由乙队施工,则需20天完成,花费
280×20=5600(元);
若由甲、乙队共同施工,则需12天完成,
花费200×12+280×12=5760(元)。
∴
按照少花钱多办事的原则,应选择由乙
队单独施工完成。
例3:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.
如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设
x多少天可以铺好这条管线.
依题意得:
,
解方程,得:
x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.
方法总结:
解这类问题常常把总工作量看作1,
工作量=人均效率×人数×时间
1、
一件工作,甲单独做需50天才能完成,乙独做需要45天完成。问在乙单独做7天以后,甲、乙合作多少天可以完成。
解:设甲、乙合作x天可以完成,依题意,得:
解得:
x
=
20
答:甲、乙合作20天可以完成。
课堂练习
2整理一批数据,由一个人做需80小时完成.现在计划由一些人做2小时,再增加5人做8小时,完成这项工作的
,怎样安排参与整理数据的具体人数?
解:设计划先由
X
人做2小时。依题意,得:
解得:
答:原计划先由2人做两小时。
练一练
3
整理一块地,一个人做需要80小时完成。现在一些人先做了2小时后,有4人因故离开,剩下的人又做了4小时完成了这项工作,假设这些人的工作效率相同,求一开始安排的人数。
各阶段的工作量之和=总工作量1
X人
X=16
3.4实际问题与一元一次方程
工程问题
学
科网
工程问题中的量及其关系:
1.工作效率:
2.工程问题中的基本关系:
工作量=
3.总工作量可看做“1”
4.合效率:各效率之和;
各部分工作量之和=工作总量
活动1.自主学习
难点强调
工作效率×工作时间
单位时间完成的工作量
知识回顾
?比一比,赛一赛.
看谁做得好,看谁做得快!
1.一项工作甲独做5天完成,乙独做10天完成,
那么甲每天的工作效率是
,
乙每天的工作效率是
,
两人合作1天完成的工作量是
,
两人合作3天完成的工作量是
.
一件工作,甲单独做x小时完成,乙单
独做y小时完成,那么甲、乙的工作效率分
别为???
????、????
???;甲、乙合作m天可以完成
的工作量为???
?
或
???。
引例:
请同学们模仿例1的分析思路,完成例2的题目分析解答.
例1
整理一批图书,由一个人做要40
h完成.现在计划由一部分人先做4
h,再增加
2人和他们一起做8
h,完成这项工作.假设这些人的工作效率相同,具体应安排多少人工作?
总工作量
每个人的工作效率
先安排的人数
增加的人数
先安排的人的工作时间
增加的人的工作时间
先安排的人完成的工作量
增加的人完成的工作量
(1)请你一边阅读题目,一边画出文段中的关键信息,并用自己的语言概括出来.
(2)设适当的未知数,将上述问题在表格中表示出来.
1
x人
2人
(4+8)小时
(3)总的工作量如何表示呢?
8小时
两批人完成的工作量之和
解:设安排
x人先做4
h,根据题意可得
解方程得
x=2.
答:应安排2人先做4
h.
例2、某管道由甲、乙两工程队单独施工分别需要30
天、20天。
(1)如果两队从两端同时相向施工,需要多少
天铺好?
(2)又知甲队单独施工每天需付200元的施工
费,乙队单独施工每天需付280元施工费,
那么是由甲队单独施工,还是乙队单独施
工,还是两队同时施工,请你按照少花钱
多办事的原则,设计一个方案,并说明理
由。
巩固练习
解:(1)设需要
x
天铺好,依题意,得:
解得:
x
=
12
∴
需要12天铺好。
(2)若单独由甲队施工,则需30天完成,花费
200×30=6000(元);
若单独由乙队施工,则需20天完成,花费
280×20=5600(元);
若由甲、乙队共同施工,则需12天完成,
花费200×12+280×12=5760(元)。
∴
按照少花钱多办事的原则,应选择由乙
队单独施工完成。
例3:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.
如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设
x多少天可以铺好这条管线.
依题意得:
,
解方程,得:
x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.
方法总结:
解这类问题常常把总工作量看作1,
工作量=人均效率×人数×时间
1、
一件工作,甲单独做需50天才能完成,乙独做需要45天完成。问在乙单独做7天以后,甲、乙合作多少天可以完成。
解:设甲、乙合作x天可以完成,依题意,得:
解得:
x
=
20
答:甲、乙合作20天可以完成。
课堂练习
2整理一批数据,由一个人做需80小时完成.现在计划由一些人做2小时,再增加5人做8小时,完成这项工作的
,怎样安排参与整理数据的具体人数?
解:设计划先由
X
人做2小时。依题意,得:
解得:
答:原计划先由2人做两小时。
练一练
3
整理一块地,一个人做需要80小时完成。现在一些人先做了2小时后,有4人因故离开,剩下的人又做了4小时完成了这项工作,假设这些人的工作效率相同,求一开始安排的人数。
各阶段的工作量之和=总工作量1
X人
X=16
