人教版数学九年级上册25.3用频率估计概率课件(16张)
文档属性
| 名称 | 人教版数学九年级上册25.3用频率估计概率课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 316.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
25.3用频率估计概率
学习目标
1、知道利用频率估计概率的条件是什么?
2、掌握如何利用频率估计概率。
3、知道利用频率估计出的概率是近似值。
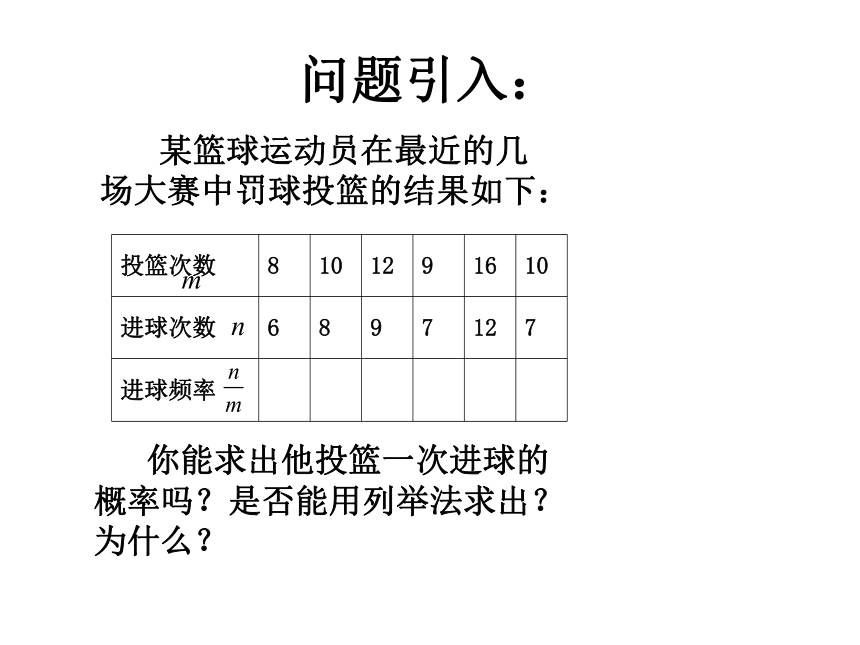
问题引入:
某篮球运动员在最近的几场大赛中罚球投篮的结果如下:
投篮次数 8 10 12 9 16 10
进球次数 6 8 9 7 12 7
进球频率
你能求出他投篮一次进球的概率吗?是否能用列举法求出?为什么?
知识回顾
用列举法求概率的条件是什么
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢
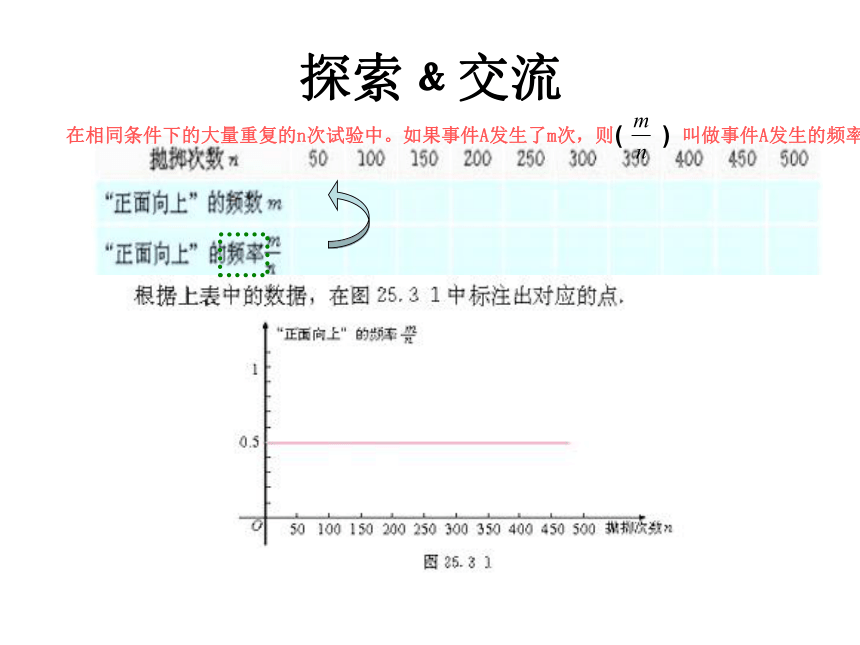
探索﹠交流
在相同条件下的大量重复的n次试验中。如果事件A发生了m次,则 叫做事件A发生的频率.
( )
归纳
一般地,在大量重复试验中,如果事件A发生的频率 稳定于某个常数 ,那么事件A发生的概率
P(A)=
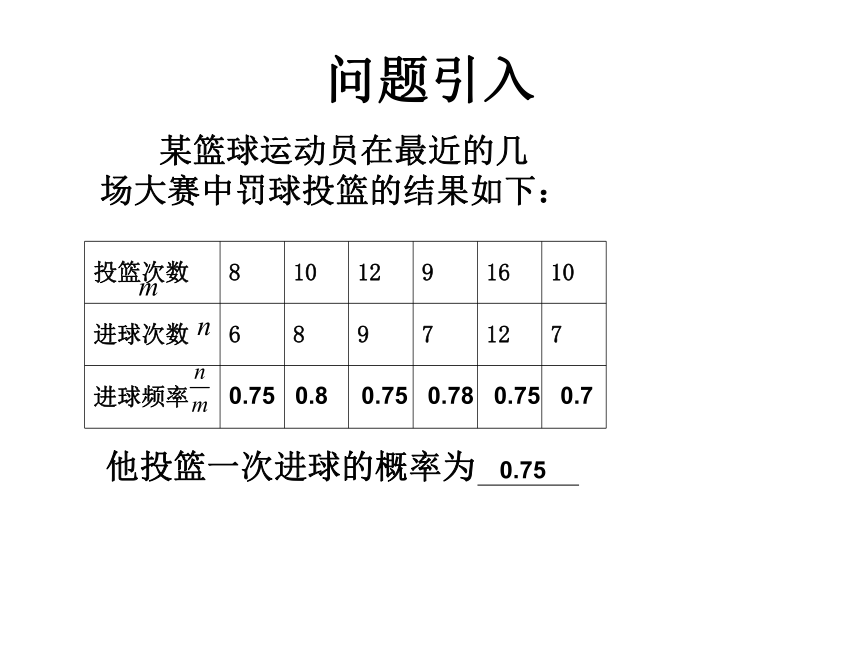
问题引入
某篮球运动员在最近的几场大赛中罚球投篮的结果如下:
投篮次数 8 10 12 9 16 10
进球次数 6 8 9 7 12 7
进球频率
他投篮一次进球的概率为
0.75 0.8 0.75 0.78 0.75 0.7
0.75
思考
对于一个随机事件A,用频率估计的概率P(A)可能小于0吗?可能大于1吗?
某林业部门要考查某种幼树在一定条件下的移植成活率,应
采用什么具体做法
观察在各次试验中得到的幼树成活的频率,谈谈
你的看法.
估计移植成活率
移植总数(n) 成活数(m)
10 8
成活的频率
0.8
( )
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
是实际问题中的一种概率,可理解为成活的概率.
估计移植成活率
由下表可以发现,幼树移植成活的频率在____左右摆动,
并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为_____.
0.9
0.9
移植总数(n) 成活数(m)
10 8
成活的频率
0.8
( )
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
由下表可以发现,幼树移植成活的频率在____左右摆动,
并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为_____.
0.9
0.9
移植总数(n) 成活数(m)
10 8
成活的频率
0.8
( )
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
1.林业部门种植了该幼树1000棵,估计能成活_______棵.
2.我们学校需种植这样的树苗500棵来绿化校园,则至少
向林业部门购买约_______棵.
900
556
估计移植成活率
练一练
则估计油菜籽发芽的概率为___
0.9
练一练
一水塘里有鲤鱼、鲫鱼、鲢鱼共1000条,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼_______条,鲢鱼_______条.
310
270
升华提高
了解了一种方法-------用多次试验频率去估计概率
体会了一种思想:
弄清了一种关系------频率与概率的关系
当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
用样本去估计总体
用频率去估计概率
作业:
习题25.3第1、2、3、5题
25.3用频率估计概率
学习目标
1、知道利用频率估计概率的条件是什么?
2、掌握如何利用频率估计概率。
3、知道利用频率估计出的概率是近似值。
问题引入:
某篮球运动员在最近的几场大赛中罚球投篮的结果如下:
投篮次数 8 10 12 9 16 10
进球次数 6 8 9 7 12 7
进球频率
你能求出他投篮一次进球的概率吗?是否能用列举法求出?为什么?
知识回顾
用列举法求概率的条件是什么
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢
探索﹠交流
在相同条件下的大量重复的n次试验中。如果事件A发生了m次,则 叫做事件A发生的频率.
( )
归纳
一般地,在大量重复试验中,如果事件A发生的频率 稳定于某个常数 ,那么事件A发生的概率
P(A)=
问题引入
某篮球运动员在最近的几场大赛中罚球投篮的结果如下:
投篮次数 8 10 12 9 16 10
进球次数 6 8 9 7 12 7
进球频率
他投篮一次进球的概率为
0.75 0.8 0.75 0.78 0.75 0.7
0.75
思考
对于一个随机事件A,用频率估计的概率P(A)可能小于0吗?可能大于1吗?
某林业部门要考查某种幼树在一定条件下的移植成活率,应
采用什么具体做法
观察在各次试验中得到的幼树成活的频率,谈谈
你的看法.
估计移植成活率
移植总数(n) 成活数(m)
10 8
成活的频率
0.8
( )
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
是实际问题中的一种概率,可理解为成活的概率.
估计移植成活率
由下表可以发现,幼树移植成活的频率在____左右摆动,
并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为_____.
0.9
0.9
移植总数(n) 成活数(m)
10 8
成活的频率
0.8
( )
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
由下表可以发现,幼树移植成活的频率在____左右摆动,
并且随着移植棵数越来越大,这种规律愈加明显.
所以估计幼树移植成活的概率为_____.
0.9
0.9
移植总数(n) 成活数(m)
10 8
成活的频率
0.8
( )
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
0.94
0.923
0.883
0.905
0.897
1.林业部门种植了该幼树1000棵,估计能成活_______棵.
2.我们学校需种植这样的树苗500棵来绿化校园,则至少
向林业部门购买约_______棵.
900
556
估计移植成活率
练一练
则估计油菜籽发芽的概率为___
0.9
练一练
一水塘里有鲤鱼、鲫鱼、鲢鱼共1000条,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼_______条,鲢鱼_______条.
310
270
升华提高
了解了一种方法-------用多次试验频率去估计概率
体会了一种思想:
弄清了一种关系------频率与概率的关系
当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
用样本去估计总体
用频率去估计概率
作业:
习题25.3第1、2、3、5题
同课章节目录
