2020-2021学年苏科版七年级数学上册期末专题复习:第3章《代数式》试题精选(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学上册期末专题复习:第3章《代数式》试题精选(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 89.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 18:28:09 | ||
图片预览



文档简介
第3章《代数式》试题精选(1)
一.选择题(共19小题)
1.(2019秋?邗江区校级期末)下列各组代数式中,是同类项的是( )
A.5x2y与xy
B.83与x3
C.5ax2与yx2
D.﹣5x2y与yx2
2.(2019秋?崇川区校级期末)“双12”前,某微商店在京东以a元每个的价格购进充电宝50个,后又从天猫以b元每个的价格购进相同型号的充电宝30个(a>b),“双12”时以0.5(a+b)元每个的价格在平台全部卖出,则该微商( )
A.亏损了
B.盈利了
C.不亏不盈
D.亏损还是盈利由a,b的值决定
3.(2019秋?姑苏区期末)已知关于x的多项式﹣2x3+6x2+9x+1﹣(3ax2﹣5x+3)的取值不含x2项,那么a的值是( )
A.﹣3
B.3
C.﹣2
D.2
4.(2019秋?姑苏区期末)如果a和1﹣4b互为相反数,那么多项式2(b﹣2a+10)+7(a﹣2b﹣3)的值是( )
A.﹣4
B.﹣2
C.2
D.4
5.(2019秋?盐都区期末)无论x取什么值,代数式的值一定是正数的是( )
A.(x+2)2
B.|x+2|
C.x2+2
D.x2﹣2
6.(2019秋?铜山区期末)下列运算中,结果正确的是( )
A.4+5ab=9ab
B.6xy﹣y=5xy
C.3ab﹣3ba=0
D.12x3+4x4=16x7
7.(2019秋?崇川区校级期末)A和B都是三次多项式,则A+B一定是( )
A.三次多项式
B.次数不高于3的整式
C.次数不高于3的多项式
D.次数不低于3的整式
8.(2019秋?海陵区校级期末)下列不是同类项的是( )
A.﹣ab3与b3a
B.12与0
C.2xyz与﹣zyx
D.3x2y与﹣6xy2
9.(2019秋?海陵区校级期末)已知a+4b,那么代数式9(a+2b)﹣2(2a﹣b)的值是( )
A.
B.﹣1
C.
D.1
10.(2019秋?海安市期末)若x,y满足等式x2﹣2x=2y﹣y2,且xy,则式子x2+2xy+y2﹣2(x+y)+2019的值为( )
A.2018
B.2019
C.2020
D.2021
11.(2019秋?溧阳市期末)下列计算正确的是( )
A.2a+3b=5ab
B.5a2b﹣2a2b=3a2b
C.5a﹣3a=2
D.6a+a=6a2
12.(2019秋?清江浦区期末)按图中程序计算,若输出的值为9,则输入的数是( )
A.289
B.2
C.﹣1
D.2或﹣1
13.(2019秋?常熟市期末)多项式m3n4﹣5m3n5+3的项数和次数分别为( )
A.2,7
B.3,8
C.2,8
D.3,7
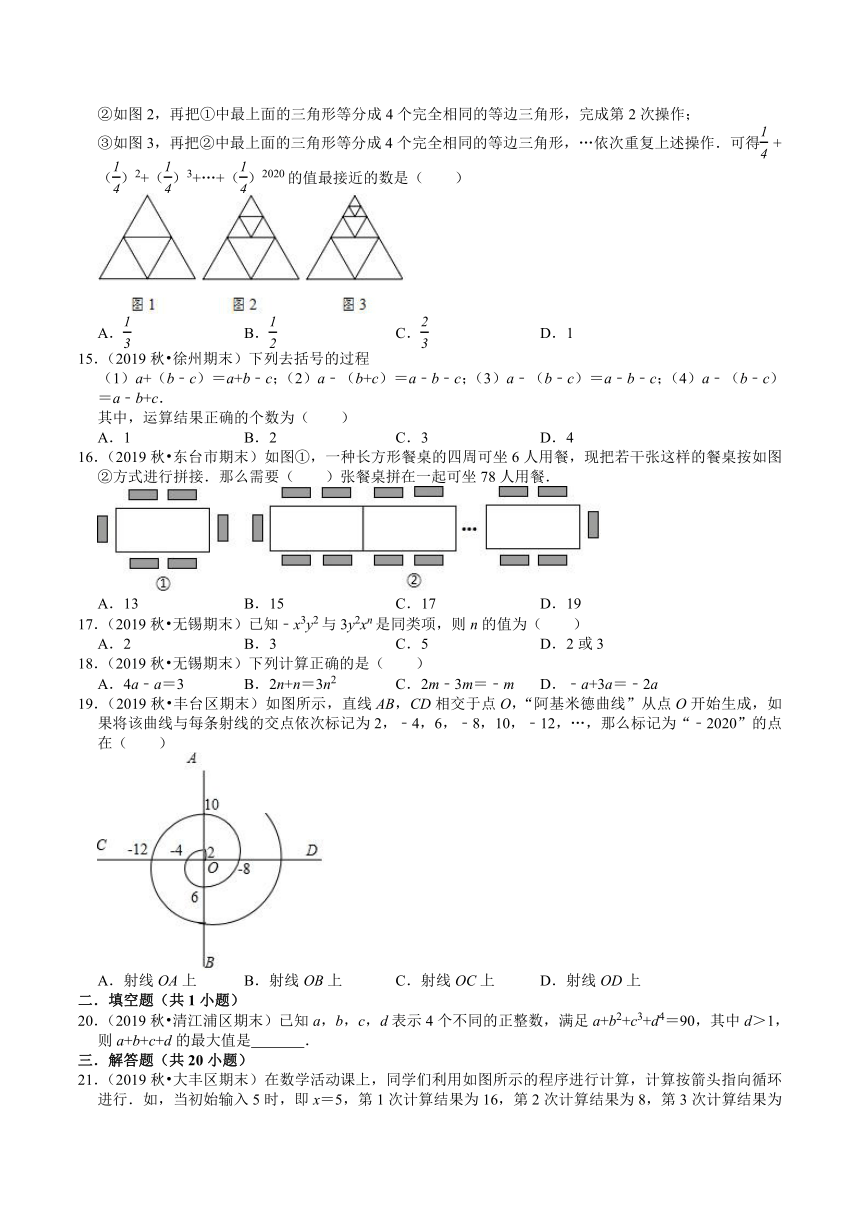
14.(2019秋?鼓楼区期末)小红在计算()2+()3+…+()2020时,拿出1张等边三角形纸片按如图所示方式进行操作.
①如图1,把1个等边三角形等分成4个完全相同的等边三角形,完成第1次操作;
②如图2,再把①中最上面的三角形等分成4个完全相同的等边三角形,完成第2次操作;
③如图3,再把②中最上面的三角形等分成4个完全相同的等边三角形,…依次重复上述操作.可得()2+()3+…+()2020的值最接近的数是( )
A.
B.
C.
D.1
15.(2019秋?徐州期末)下列去括号的过程
(1)a+(b﹣c)=a+b﹣c;(2)a﹣(b+c)=a﹣b﹣c;(3)a﹣(b﹣c)=a﹣b﹣c;(4)a﹣(b﹣c)=a﹣b+c.
其中,运算结果正确的个数为( )
A.1
B.2
C.3
D.4
16.(2019秋?东台市期末)如图①,一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图②方式进行拼接.那么需要( )张餐桌拼在一起可坐78人用餐.
A.13
B.15
C.17
D.19
17.(2019秋?无锡期末)已知﹣x3y2与3y2xn是同类项,则n的值为( )
A.2
B.3
C.5
D.2或3
18.(2019秋?无锡期末)下列计算正确的是( )
A.4a﹣a=3
B.2n+n=3n2
C.2m﹣3m=﹣m
D.﹣a+3a=﹣2a
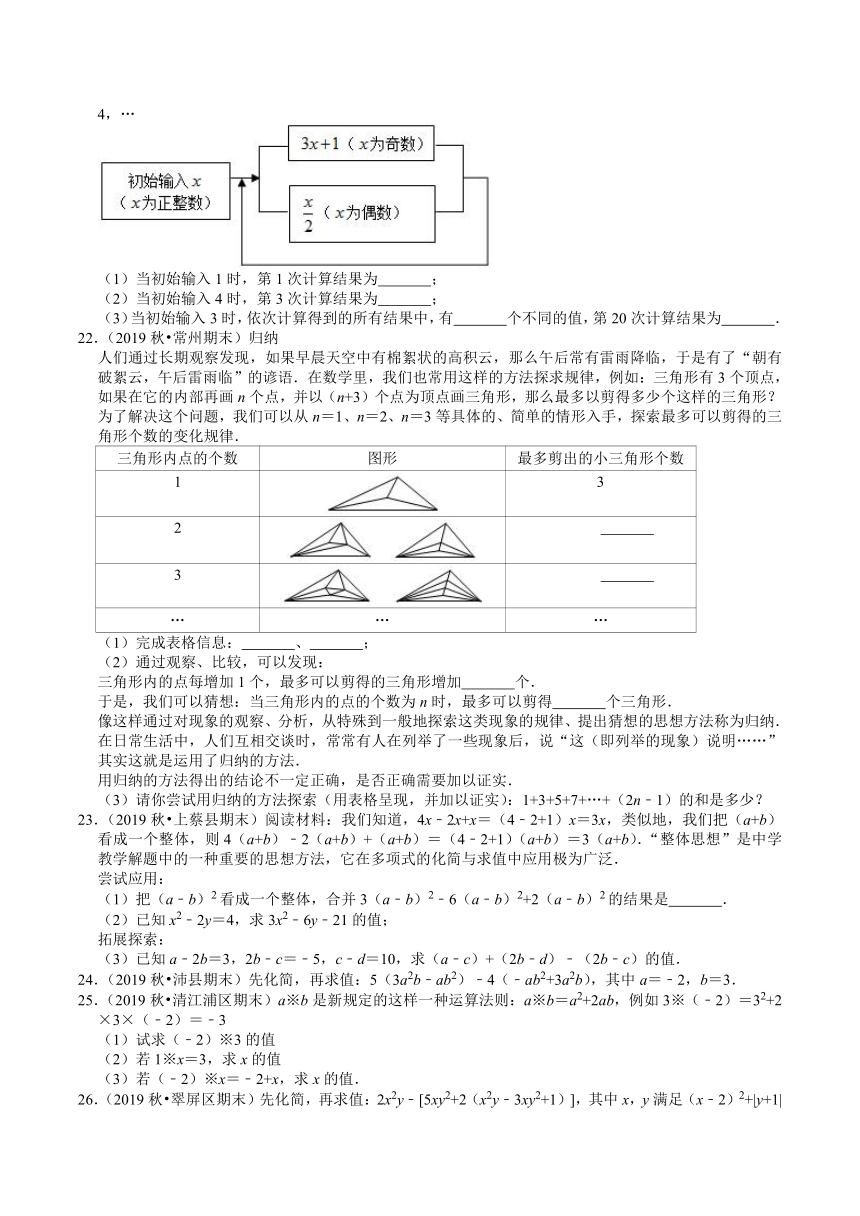
19.(2019秋?丰台区期末)如图所示,直线AB,CD相交于点O,“阿基米德曲线”从点O开始生成,如果将该曲线与每条射线的交点依次标记为2,﹣4,6,﹣8,10,﹣12,…,那么标记为“﹣2020”的点在( )
A.射线OA上
B.射线OB上
C.射线OC上
D.射线OD上
二.填空题(共1小题)
20.(2019秋?清江浦区期末)已知a,b,c,d表示4个不同的正整数,满足a+b2+c3+d4=90,其中d>1,则a+b+c+d的最大值是
.
三.解答题(共20小题)
21.(2019秋?大丰区期末)在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.如,当初始输入5时,即x=5,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,…
(1)当初始输入1时,第1次计算结果为
;
(2)当初始输入4时,第3次计算结果为
;
(3)当初始输入3时,依次计算得到的所有结果中,有
个不同的值,第20次计算结果为
.
22.(2019秋?常州期末)归纳
人们通过长期观察发现,如果早晨天空中有棉絮状的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学里,我们也常用这样的方法探求规律,例如:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点画三角形,那么最多以剪得多少个这样的三角形?
为了解决这个问题,我们可以从n=1、n=2、n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
三角形内点的个数
图形
最多剪出的小三角形个数
1
3
2
3
…
…
…
(1)完成表格信息:
、
;
(2)通过观察、比较,可以发现:
三角形内的点每增加1个,最多可以剪得的三角形增加
个.
于是,我们可以猜想:当三角形内的点的个数为n时,最多可以剪得
个三角形.
像这样通过对现象的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
在日常生活中,人们互相交谈时,常常有人在列举了一些现象后,说“这(即列举的现象)说明……”其实这就是运用了归纳的方法.
用归纳的方法得出的结论不一定正确,是否正确需要加以证实.
(3)请你尝试用归纳的方法探索(用表格呈现,并加以证实):1+3+5+7+…+(2n﹣1)的和是多少?
23.(2019秋?上蔡县期末)阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是
.
(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值;
拓展探索:
(3)已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
24.(2019秋?沛县期末)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a=﹣2,b=3.
25.(2019秋?清江浦区期末)a※b是新规定的这样一种运算法则:a※b=a2+2ab,例如3※(﹣2)=32+2×3×(﹣2)=﹣3
(1)试求(﹣2)※3的值
(2)若1※x=3,求x的值
(3)若(﹣2)※x=﹣2+x,求x的值.
26.(2019秋?翠屏区期末)先化简,再求值:2x2y﹣[5xy2+2(x2y﹣3xy2+1)],其中x,y满足(x﹣2)2+|y+1|=0.
27.(2019秋?崇川区校级期末)计算或简化
(1)﹣44﹣()×[4﹣(﹣2)2]﹣1
(2)18﹣6÷(﹣2)3×()
(3)2a﹣(5b﹣a)+b
(4)﹣[2m﹣3(m﹣n+1)﹣2]﹣1
28.(2019秋?崇川区期末)观察下列等式:;;;……根据上面等式反映的规律,解答下列问题:
(1)请根据上述等式的特征,在括号内填上同一个实数:2×
﹣5=
×5;
(2)小明将上述等式的特征用字母表示为:2x﹣y=xy(x、y为任意实数).
①小明和同学讨论后发现:x、y的取值范围不能是任意实数.请你直接写出x、y不能取哪些实数.
②是否存在x、y两个实数都是整数的情况?若存在,请求出x、y的值;若不存在,请说明理由.
29.(2019秋?海安市期末)有以下运算程序,如图所示:
比如,输入数对(2,1),输出W=2.
(1)若输入数对(1,﹣2),则输出W=
;
(2)分别输入数对(m,﹣n)和(﹣n,m),输出的结果分别是W1,W2,试比较W1,W2的大小,并说明理由;
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W=26,求a+b的值.
30.(2019秋?海安市期末)计算.
(1)4×()÷(﹣2)
(2)()×(﹣36)
(3)﹣1?+(1﹣0.5)÷(﹣3)×[2﹣(﹣3)2]
(4)2(a2﹣ab)+3(a2﹣ab)+4ab
31.(2019秋?盐都区期末)先化简,再求值:3x2+(2xy﹣3y2)﹣2(x2+xy﹣y2),其中x=﹣1,y=2.
32.(2019秋?盐都区期末)化简:
(1)﹣3x+2y+5x﹣7y;
(2)2(x2﹣2x)﹣(2x2+3x).
33.(2019秋?盐都区期末)已知:如图,点P是数轴上表示﹣2与﹣1两数的点为端点的线段的中点.
(1)数轴上点P表示的数为
;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为
;
(3)如图,若点P是线段AB(点A在点B的左侧)的中点,且点A表示的数为m,那么点B表示的数是
.(用含m的代数式表示)
34.(2019秋?建邺区期末)先化简,再求值:2(3x2y+xy2)﹣3(2x2y﹣xy)﹣2xy2+1,其中x,y=1.
35.(2019秋?东海县期末)计算:
(1)5﹣32÷(﹣3);
(2);
(3)2m﹣3n﹣5n﹣7m;
(4)x2﹣[﹣4xy+(xy﹣x2)]﹣2xy.
36.(2019秋?铜山区期末)合并下列各式中的同类项:
(1)3x2﹣1﹣2x﹣5+3x﹣x2
(2)(2a2﹣4a+1)﹣(﹣3a2+2a﹣5)
37.(2019秋?镇江期末)求5(3a2b﹣ab2)﹣4(﹣ab2+3a2b)的值,其中a,b满足|a+2|+(b﹣3)2=0.
38.(2019秋?金湖县期末)先化简,再求值:3a2+b2﹣2(6a2﹣b2),其中a=﹣2,b=3.
39.(2019秋?高邮市期末)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a、b满足(a﹣1)2与|b|互为相反数.
40.(2019秋?沭阳县期末)在一条直路上的A、B、C、D四个车站的位置如图所示(单位千米),如果小明家在A站旁,他的同学小亮家在B站旁,新华书店在D站旁,一天小明乘车从A站出发到D站下车去新华书店购买一些课外阅读书籍,途径B、C两站,当小明到达C站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到B站处下车向小亮借足了钱,然后乘车继续赶往D站旁的新华书店.
(1)求C、D两站的距离;(用含有a、b的代数式表示)
(2)求这一天小明从A站到D站乘车路程.(用含有a、b的代数式表示)
第3章《代数式》试题精选(1)
参考答案与试题解析
一.选择题(共19小题)
1.【答案】D
【解答】解:A、相同字母的指数不尽相同,不是同类项,故A错误;
B、字母不同,不是同类项,故B错误;
C、字母不尽相同,不是同类项,故C错误;
D、字母相同且相同字母的指数也相同,故D正确;
故选:D.
2.【答案】A
【解答】解:∵某微商店在京东以a元每个的价格购进充电宝50个,后又从天猫以b元每个的价格购进相同型号的充电宝30个(a>b),
∴每个充电宝的平均进价为:,
∵“双12”时以0.5(a+b)元每个的价格在平台全部卖出,
∴,
∵a>b,
∴b﹣a<0,
∴该微商亏损了.
故选:A.
3.【答案】D
【解答】解:﹣2x3+6x2+9x+1﹣(3ax2﹣5x+3)
=﹣2x3+6x2+9x+1﹣3ax2+5x﹣3
=﹣2x3+(6﹣3a)x2+14x﹣2,
∵关于x的多项式﹣2x3+6x2+9x+1﹣(3ax2﹣5x+3)的取值不含x2项,
∴6﹣3a=0,
解得:a=2.
故选:D.
4.【答案】A
【解答】解:由题意可知:a+1﹣4b=0,
∴a﹣4b=﹣1,
∴原式=2b﹣4a+20+7a﹣14b﹣21
=3a﹣12b﹣1
=3(a﹣4b)﹣1
=﹣3﹣1
=﹣4,
故选:A.
5.【答案】C
【解答】解:A、当x=﹣2时,代数式x+2的值为0,不符合题意;
B、当x=﹣2时,代数式|x+2|的值为0,0不是正数,所以错误;
C、无论x是何值,代数式x2+2的值都是正数.
D、当x=0时,代数式x2﹣2的值为﹣2,不符合题意;
故选:C.
6.【答案】C
【解答】解:A、4+5ab≠9ab,故此选项错误;
B、6xy﹣y,无法计算,故此选项错误;
C、3ab﹣3ba=0,故此选项正确;
D、12x3+4x4,无法计算,故此选项错误;
故选:C.
7.【答案】B
【解答】解:A和B都是三次多项式,则A+B一定是次数不高于3的整式,
故选:B.
8.【答案】D
【解答】解:A.﹣ab3与b3a,字母相同,字母的次数也相同,故是同类项,不符合题意;
B.12与0是常数,故是同类项,不符合题意;
C.2xyz与﹣zyx,字母相同,字母的次数也相同,故是同类项,不符合题意;
D.3x2y与﹣6xy2,字母相同,字母的次数不相同,故不是同类项,符合题意;
故选:D.
9.【答案】B
【解答】解:当a+4b,
9(a+2b)﹣2(2a﹣b)
=5a+20b
=5(a+4b)
=5×()
=﹣1,
故选:B.
10.【答案】C
【解答】解:∵x2﹣2x=2y﹣y2,xy,
∴x2﹣2x+y2﹣2y=0,2xy=1,
∴x2+2xy+y2﹣2(x+y)+2019=x2﹣2x+y2﹣2y+1+2019=2020,
故选:C.
11.【答案】B
【解答】解:A.2a与3b不是同类项,不能合并,此选项错误;
B.5a2b﹣2a2b=(5﹣2)a2b=3a2b,此选项正确;
C.5a﹣3a=(5﹣3)a=2a,此选项错误;
D.6a+a=(6+1)a=7a,此选项错误;
故选:B.
12.【答案】D
【解答】解:±±3,
∴输入的数是:
(﹣3+1)÷2
=﹣2÷2
=﹣1
(3+1)÷2
=4÷2
=2
故选:D.
13.【答案】B
【解答】解:m3n4﹣5m3n5+3是八次三项式,故项数是3,次数是8.
故选:B.
14.【答案】A
【解答】解:设S()2+()3+…+()2020,
则4S=1()2+()3+…+()2019,
4S﹣S=1﹣()2020,
3S=1﹣()2020,
S,
故选:A.
15.【答案】C
【解答】解:(1)a+(b﹣c)=a+b﹣c,故此题正确;
(2)a﹣(b+c)=a﹣b﹣c,故此题正确;
(3)a﹣(b﹣c)=a﹣b+c,故此题错误;
(4)a﹣(b﹣c)=a﹣b+c,故此题正确.
所以运算结果正确的个数为3个,
故选:C.
16.【答案】D
【解答】解:根据图形的变化可知:
一种长方形餐桌的四周可坐6人用餐,即4×1+2=6;
2种长方形餐桌的四周可坐6人用餐,即4×2+2=10;
3种长方形餐桌的四周可坐6人用餐,即4×3+2=14;
…
发现规律:
n种长方形餐桌的四周可坐6人用餐,即4n+2;
∴4n+2=78.
解得n=19.
所以需要19张餐桌拼在一起可坐78人用餐.
故选:D.
17.【答案】B
【解答】解:∵﹣x3y2与3y2xn是同类项,
∴n=3,
故选:B.
18.【答案】C
【解答】解:A、结果是3a,故本选项错误;
B、结果是3n,故本选项错误;
C、结果是﹣m,故本选项正确;
D、结果是2a,故本选项错误;
故选:C.
19.【答案】C
【解答】解:观察图形的变化可知:
奇数项:2、6、10、14…4n﹣2(n为正整数);
偶数项:﹣4、﹣8、﹣12、﹣16…﹣4n.
∵﹣2020是偶数项,
∴﹣4n=﹣2020,
∴n=505.
∵每四条射线为一组,OC为始边,
∴505÷4=126…1.
∴标记为“﹣2020”的点在射线OC上.
故选:C.
二.填空题(共1小题)
20.【答案】70.
【解答】解:要使a+b+c+d的值最大,
此时d>1,
要使a+b+c+d有最大值,且a+b2+c3+d4=90,
∴b,c,d尽可能取最小,
∴d=2,c=1,b=3,
a=90﹣(b2+c3+d4)=90﹣(9+1+16)=64,
故a+b+c+d的最大值是64+3+2+1=70.
故答案为:70.
三.解答题(共20小题)
21.【答案】见试题解答内容
【解答】解:(1)当x=1时,3x+1=4,
故答案为:4;
(2)当x=4时,第1次结果为:2,第2次结果为1,第3次结果为3x+1=4;
故答案为:4;
(3)当x=3时,
第1次结果为:3x+1=10,第2次结果为5,第3次结果为3x+1=16;第4次结果为8,
第5次结果为4,第6次结果为2,第7次结果为1,
第8次结果为3x+1=4,……
∵(20﹣4)÷3=5……1,
∴第20次运算的结果为4.
∴有7个不同的值,
故答案为:7,4.
22.【答案】见试题解答内容
【解答】解;(1)由图形规律可得,答案为5,7;
(2)∵5﹣3=7﹣5=2,
∴三角形内的点每增加1个,最多可以剪得的三角形增加2个;
∵三角形内点的个数为1时,最多剪出的小三角形个数3=2×1+1,
三角形内点的个数为2时,最多剪出的小三角形个数5=2×2+1,
三角形内点的个数为3时,7最多剪出的小三角形个数7=2×3+1,
∴三角形内点的个数为n时,最多剪出的小三角形个数2n+1.
故答案为2,(2n+1);
(3)
加数的个数
和
1+3
22
1+3+5
32
1+3+5+7
42
…
…
1+3+5+7+…+(2n﹣1)
n2
证明:∵S=1+3+5+7+…+(2n﹣5)+(2n﹣3)+(2n﹣1)
∴S=(2n﹣1)+(2n﹣3)+(2n﹣5)+…+7+5+3+1
∴S+S=2n?n=2n2
2S=2n2
S=n2
23.【答案】见试题解答内容
【解答】解:(1)∵3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2=(3﹣6+2)(a﹣b)2=﹣(a﹣b)2;
故答案为:﹣(a﹣b)2;
(2)∵x2﹣2y=4,
∴原式=3(x2﹣2y)﹣21=12﹣21=﹣9;
(3)∵a﹣2b=3①,2b﹣c=﹣5②,c﹣d=10③,
由①+②可得a﹣c=﹣2,
由②+③可得2b﹣d=5,
∴原式=﹣2+5﹣(﹣5)=8.
24.【答案】见试题解答内容
【解答】解:原式=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2,
当a=﹣2,b=3时,原式=36+18=54.
25.【答案】见试题解答内容
【解答】解:(1)(﹣2)※3=(﹣2)2+2×(﹣2)×3=4﹣12=﹣8;
(2)∵1※x=3,
∴12+2x=3,
∴2x=3﹣1,
∴x=1;
(3)﹣2※x=﹣2+x,
(﹣2)2+2×(﹣2)x=﹣2+x,
4﹣4x=﹣2+x,
﹣4x﹣x=﹣2﹣4,
﹣5x=﹣6,
x.
26.【答案】见试题解答内容
【解答】解:原式=2x2y﹣[5xy2+2x2y﹣6xy2+2]
=2x2y﹣5xy2﹣2x2y+6xy2﹣2
=xy2﹣2,
由(x﹣2)2+|y+1|=0,得到x=2,y=﹣1,
则原式=2×(﹣1)2﹣2=2﹣2=0.
27.【答案】见试题解答内容
【解答】解:(1)原式=﹣256﹣()×0﹣1
=﹣256﹣1
=﹣257;
(2)原式=18﹣6×()×()
=18
;
(3)原式=2a﹣5b+a+b
=3a﹣4b;
(4))﹣[2m﹣3(m﹣n+1)﹣2]﹣1
=﹣2m+3(m﹣n+1)+2﹣1
=﹣2m+3m﹣3n+3+2﹣1
=m﹣3n+4.
28.【答案】见试题解答内容
【解答】解:(1)设所求数为x,
由已知等式可得,2x﹣5=5x,
∴x,
故答案为,;
(2)①∵2x﹣y=xy,
∴2x=y(1+x),
当x=﹣1时,等式不成立,
当y=2时,2x=2+2x,等式不成立,
∴x≠﹣1,y≠2;
②y2,
当1+x=±2时,x=1或x=﹣3,y=1或y=3;
当1+x=±1时,x=0或x=﹣2,y=0或y=4.
29.【答案】见试题解答内容
【解答】解:(1)输入数对(1,﹣2),即a=1,b=﹣2,
W=[|a﹣b|+(a+b)]1.
故答案为:1.
(2)当a=m,b=﹣n时,W1=[|a﹣b|+(a+b)][|m+n|+(m﹣n)].
当a=﹣n,b=m时,W2=[|a﹣b|+(a+b)][|﹣n﹣m|+(m﹣n)][|m+n|+(m﹣n)].
即W1=W2;
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W.
①当x≥3时,W[x﹣2﹣(x﹣3)+(x﹣2)+(x﹣3)](2x﹣4)=26
解得x=28,
则a+b=x﹣2+x﹣3=51;
②当2≤x<3时,W[|x﹣2﹣(3﹣x)|+(x﹣2)﹣(x﹣3)]=26
x=28或﹣23(均不合题意舍去);
③当x<2时,W[|2﹣x﹣(3﹣x)|﹣(x﹣2)﹣(x﹣3)](﹣4x+10)=26,
解得x=﹣23,
则a+b=51.
综上所述,a+b的值为51.
30.【答案】见试题解答内容
【解答】解:(1)原式=﹣2÷(﹣2)=1;
(2)原式(﹣36)(﹣36)(﹣36),
=18﹣27+8,
=﹣1;
(3)原式=﹣1()×(2﹣9),
=﹣1()×(﹣7),
=﹣1,
;
(4)原式=2a2﹣2ab+2a2﹣3ab+4ab,
=4a2﹣ab.
31.【答案】见试题解答内容
【解答】解:原式=3x2+2xy﹣3y2﹣2x2﹣2xy+2y2=x2﹣y2,
当x=﹣1,y=2时,原式=1﹣4=﹣3.
32.【答案】见试题解答内容
【解答】解:(1)原式=2x﹣5y;
(2)原式=2x2﹣4x﹣2x2﹣3x=﹣7x.
33.【答案】见试题解答内容
【解答】解:(1)由题意可得,
数轴上点P表示的数为:1.5,
故答案为:﹣1.5;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为:﹣1.5+2.5=1或﹣1.5﹣2.5=﹣4,
故答案为:1或﹣4;
(3)设点B表示的数为b,
则﹣1.5,得b=﹣3﹣m,
故答案为:﹣3﹣m.
34.【答案】见试题解答内容
【解答】解:原式=6x2y+2xy2﹣6x2y+3xy﹣2xy2+1=3xy+1,
当x,y=1时,原式=1+1=2.
35.【答案】见试题解答内容
【解答】解:(1)原式=5﹣9÷(﹣3)=5+3=8;
(2)原式=﹣1﹣2+12=9;
(3)原式=﹣5m﹣8n;
(4)原式=x2+4xy﹣(xy﹣x2)﹣2xy
=x2+4xy﹣xy+x2﹣2xy
=2x2+xy.
36.【答案】见试题解答内容
【解答】解:(1)原式=2x2+x﹣6;
(2)原式=2a2﹣4a+1+3a2﹣2a+5,
=5a2﹣6a+6.
37.【答案】见试题解答内容
【解答】解:原式=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2,
由|a+2|+(b﹣3)2=0,得到a+2=0,b﹣3=0,
解得:a=﹣2,b=3,
则原式=36+18=54.
38.【答案】见试题解答内容
【解答】解:原式=3a2+b2﹣12a2+2b2=﹣9a2+3b2,
当a=﹣2,b=3时,原式=﹣36+27=﹣9.
39.【答案】见试题解答内容
【解答】解:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b)=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2=ab(3a﹣b),
∵(a﹣1)2与|b|互为相反数,
∴(a﹣1)2+|b|=0
∴a=2,b,
∴原式=﹣(6).
40.【答案】见试题解答内容
【解答】解:(1)由题意得:(3a+2b)﹣(2a﹣b)=3a+2b﹣2a+b=a+3b,
答:C、D两站的距离为(a+3b)千米.
(2)(a+b)+2(2a﹣b)+(3a+2b)=a+b+4a﹣2b+3a+2b=8a+b
答:小明从A站到D站乘车路程共计(8a+b)千米.
一.选择题(共19小题)
1.(2019秋?邗江区校级期末)下列各组代数式中,是同类项的是( )
A.5x2y与xy
B.83与x3
C.5ax2与yx2
D.﹣5x2y与yx2
2.(2019秋?崇川区校级期末)“双12”前,某微商店在京东以a元每个的价格购进充电宝50个,后又从天猫以b元每个的价格购进相同型号的充电宝30个(a>b),“双12”时以0.5(a+b)元每个的价格在平台全部卖出,则该微商( )
A.亏损了
B.盈利了
C.不亏不盈
D.亏损还是盈利由a,b的值决定
3.(2019秋?姑苏区期末)已知关于x的多项式﹣2x3+6x2+9x+1﹣(3ax2﹣5x+3)的取值不含x2项,那么a的值是( )
A.﹣3
B.3
C.﹣2
D.2
4.(2019秋?姑苏区期末)如果a和1﹣4b互为相反数,那么多项式2(b﹣2a+10)+7(a﹣2b﹣3)的值是( )
A.﹣4
B.﹣2
C.2
D.4
5.(2019秋?盐都区期末)无论x取什么值,代数式的值一定是正数的是( )
A.(x+2)2
B.|x+2|
C.x2+2
D.x2﹣2
6.(2019秋?铜山区期末)下列运算中,结果正确的是( )
A.4+5ab=9ab
B.6xy﹣y=5xy
C.3ab﹣3ba=0
D.12x3+4x4=16x7
7.(2019秋?崇川区校级期末)A和B都是三次多项式,则A+B一定是( )
A.三次多项式
B.次数不高于3的整式
C.次数不高于3的多项式
D.次数不低于3的整式
8.(2019秋?海陵区校级期末)下列不是同类项的是( )
A.﹣ab3与b3a
B.12与0
C.2xyz与﹣zyx
D.3x2y与﹣6xy2
9.(2019秋?海陵区校级期末)已知a+4b,那么代数式9(a+2b)﹣2(2a﹣b)的值是( )
A.
B.﹣1
C.
D.1
10.(2019秋?海安市期末)若x,y满足等式x2﹣2x=2y﹣y2,且xy,则式子x2+2xy+y2﹣2(x+y)+2019的值为( )
A.2018
B.2019
C.2020
D.2021
11.(2019秋?溧阳市期末)下列计算正确的是( )
A.2a+3b=5ab
B.5a2b﹣2a2b=3a2b
C.5a﹣3a=2
D.6a+a=6a2
12.(2019秋?清江浦区期末)按图中程序计算,若输出的值为9,则输入的数是( )
A.289
B.2
C.﹣1
D.2或﹣1
13.(2019秋?常熟市期末)多项式m3n4﹣5m3n5+3的项数和次数分别为( )
A.2,7
B.3,8
C.2,8
D.3,7
14.(2019秋?鼓楼区期末)小红在计算()2+()3+…+()2020时,拿出1张等边三角形纸片按如图所示方式进行操作.
①如图1,把1个等边三角形等分成4个完全相同的等边三角形,完成第1次操作;
②如图2,再把①中最上面的三角形等分成4个完全相同的等边三角形,完成第2次操作;
③如图3,再把②中最上面的三角形等分成4个完全相同的等边三角形,…依次重复上述操作.可得()2+()3+…+()2020的值最接近的数是( )
A.
B.
C.
D.1
15.(2019秋?徐州期末)下列去括号的过程
(1)a+(b﹣c)=a+b﹣c;(2)a﹣(b+c)=a﹣b﹣c;(3)a﹣(b﹣c)=a﹣b﹣c;(4)a﹣(b﹣c)=a﹣b+c.
其中,运算结果正确的个数为( )
A.1
B.2
C.3
D.4
16.(2019秋?东台市期末)如图①,一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图②方式进行拼接.那么需要( )张餐桌拼在一起可坐78人用餐.
A.13
B.15
C.17
D.19
17.(2019秋?无锡期末)已知﹣x3y2与3y2xn是同类项,则n的值为( )
A.2
B.3
C.5
D.2或3
18.(2019秋?无锡期末)下列计算正确的是( )
A.4a﹣a=3
B.2n+n=3n2
C.2m﹣3m=﹣m
D.﹣a+3a=﹣2a
19.(2019秋?丰台区期末)如图所示,直线AB,CD相交于点O,“阿基米德曲线”从点O开始生成,如果将该曲线与每条射线的交点依次标记为2,﹣4,6,﹣8,10,﹣12,…,那么标记为“﹣2020”的点在( )
A.射线OA上
B.射线OB上
C.射线OC上
D.射线OD上
二.填空题(共1小题)
20.(2019秋?清江浦区期末)已知a,b,c,d表示4个不同的正整数,满足a+b2+c3+d4=90,其中d>1,则a+b+c+d的最大值是
.
三.解答题(共20小题)
21.(2019秋?大丰区期末)在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.如,当初始输入5时,即x=5,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,…
(1)当初始输入1时,第1次计算结果为
;
(2)当初始输入4时,第3次计算结果为
;
(3)当初始输入3时,依次计算得到的所有结果中,有
个不同的值,第20次计算结果为
.
22.(2019秋?常州期末)归纳
人们通过长期观察发现,如果早晨天空中有棉絮状的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学里,我们也常用这样的方法探求规律,例如:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点画三角形,那么最多以剪得多少个这样的三角形?
为了解决这个问题,我们可以从n=1、n=2、n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
三角形内点的个数
图形
最多剪出的小三角形个数
1
3
2
3
…
…
…
(1)完成表格信息:
、
;
(2)通过观察、比较,可以发现:
三角形内的点每增加1个,最多可以剪得的三角形增加
个.
于是,我们可以猜想:当三角形内的点的个数为n时,最多可以剪得
个三角形.
像这样通过对现象的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
在日常生活中,人们互相交谈时,常常有人在列举了一些现象后,说“这(即列举的现象)说明……”其实这就是运用了归纳的方法.
用归纳的方法得出的结论不一定正确,是否正确需要加以证实.
(3)请你尝试用归纳的方法探索(用表格呈现,并加以证实):1+3+5+7+…+(2n﹣1)的和是多少?
23.(2019秋?上蔡县期末)阅读材料:我们知道,4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是
.
(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值;
拓展探索:
(3)已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
24.(2019秋?沛县期末)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a=﹣2,b=3.
25.(2019秋?清江浦区期末)a※b是新规定的这样一种运算法则:a※b=a2+2ab,例如3※(﹣2)=32+2×3×(﹣2)=﹣3
(1)试求(﹣2)※3的值
(2)若1※x=3,求x的值
(3)若(﹣2)※x=﹣2+x,求x的值.
26.(2019秋?翠屏区期末)先化简,再求值:2x2y﹣[5xy2+2(x2y﹣3xy2+1)],其中x,y满足(x﹣2)2+|y+1|=0.
27.(2019秋?崇川区校级期末)计算或简化
(1)﹣44﹣()×[4﹣(﹣2)2]﹣1
(2)18﹣6÷(﹣2)3×()
(3)2a﹣(5b﹣a)+b
(4)﹣[2m﹣3(m﹣n+1)﹣2]﹣1
28.(2019秋?崇川区期末)观察下列等式:;;;……根据上面等式反映的规律,解答下列问题:
(1)请根据上述等式的特征,在括号内填上同一个实数:2×
﹣5=
×5;
(2)小明将上述等式的特征用字母表示为:2x﹣y=xy(x、y为任意实数).
①小明和同学讨论后发现:x、y的取值范围不能是任意实数.请你直接写出x、y不能取哪些实数.
②是否存在x、y两个实数都是整数的情况?若存在,请求出x、y的值;若不存在,请说明理由.
29.(2019秋?海安市期末)有以下运算程序,如图所示:
比如,输入数对(2,1),输出W=2.
(1)若输入数对(1,﹣2),则输出W=
;
(2)分别输入数对(m,﹣n)和(﹣n,m),输出的结果分别是W1,W2,试比较W1,W2的大小,并说明理由;
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W=26,求a+b的值.
30.(2019秋?海安市期末)计算.
(1)4×()÷(﹣2)
(2)()×(﹣36)
(3)﹣1?+(1﹣0.5)÷(﹣3)×[2﹣(﹣3)2]
(4)2(a2﹣ab)+3(a2﹣ab)+4ab
31.(2019秋?盐都区期末)先化简,再求值:3x2+(2xy﹣3y2)﹣2(x2+xy﹣y2),其中x=﹣1,y=2.
32.(2019秋?盐都区期末)化简:
(1)﹣3x+2y+5x﹣7y;
(2)2(x2﹣2x)﹣(2x2+3x).
33.(2019秋?盐都区期末)已知:如图,点P是数轴上表示﹣2与﹣1两数的点为端点的线段的中点.
(1)数轴上点P表示的数为
;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为
;
(3)如图,若点P是线段AB(点A在点B的左侧)的中点,且点A表示的数为m,那么点B表示的数是
.(用含m的代数式表示)
34.(2019秋?建邺区期末)先化简,再求值:2(3x2y+xy2)﹣3(2x2y﹣xy)﹣2xy2+1,其中x,y=1.
35.(2019秋?东海县期末)计算:
(1)5﹣32÷(﹣3);
(2);
(3)2m﹣3n﹣5n﹣7m;
(4)x2﹣[﹣4xy+(xy﹣x2)]﹣2xy.
36.(2019秋?铜山区期末)合并下列各式中的同类项:
(1)3x2﹣1﹣2x﹣5+3x﹣x2
(2)(2a2﹣4a+1)﹣(﹣3a2+2a﹣5)
37.(2019秋?镇江期末)求5(3a2b﹣ab2)﹣4(﹣ab2+3a2b)的值,其中a,b满足|a+2|+(b﹣3)2=0.
38.(2019秋?金湖县期末)先化简,再求值:3a2+b2﹣2(6a2﹣b2),其中a=﹣2,b=3.
39.(2019秋?高邮市期末)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a、b满足(a﹣1)2与|b|互为相反数.
40.(2019秋?沭阳县期末)在一条直路上的A、B、C、D四个车站的位置如图所示(单位千米),如果小明家在A站旁,他的同学小亮家在B站旁,新华书店在D站旁,一天小明乘车从A站出发到D站下车去新华书店购买一些课外阅读书籍,途径B、C两站,当小明到达C站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到B站处下车向小亮借足了钱,然后乘车继续赶往D站旁的新华书店.
(1)求C、D两站的距离;(用含有a、b的代数式表示)
(2)求这一天小明从A站到D站乘车路程.(用含有a、b的代数式表示)
第3章《代数式》试题精选(1)
参考答案与试题解析
一.选择题(共19小题)
1.【答案】D
【解答】解:A、相同字母的指数不尽相同,不是同类项,故A错误;
B、字母不同,不是同类项,故B错误;
C、字母不尽相同,不是同类项,故C错误;
D、字母相同且相同字母的指数也相同,故D正确;
故选:D.
2.【答案】A
【解答】解:∵某微商店在京东以a元每个的价格购进充电宝50个,后又从天猫以b元每个的价格购进相同型号的充电宝30个(a>b),
∴每个充电宝的平均进价为:,
∵“双12”时以0.5(a+b)元每个的价格在平台全部卖出,
∴,
∵a>b,
∴b﹣a<0,
∴该微商亏损了.
故选:A.
3.【答案】D
【解答】解:﹣2x3+6x2+9x+1﹣(3ax2﹣5x+3)
=﹣2x3+6x2+9x+1﹣3ax2+5x﹣3
=﹣2x3+(6﹣3a)x2+14x﹣2,
∵关于x的多项式﹣2x3+6x2+9x+1﹣(3ax2﹣5x+3)的取值不含x2项,
∴6﹣3a=0,
解得:a=2.
故选:D.
4.【答案】A
【解答】解:由题意可知:a+1﹣4b=0,
∴a﹣4b=﹣1,
∴原式=2b﹣4a+20+7a﹣14b﹣21
=3a﹣12b﹣1
=3(a﹣4b)﹣1
=﹣3﹣1
=﹣4,
故选:A.
5.【答案】C
【解答】解:A、当x=﹣2时,代数式x+2的值为0,不符合题意;
B、当x=﹣2时,代数式|x+2|的值为0,0不是正数,所以错误;
C、无论x是何值,代数式x2+2的值都是正数.
D、当x=0时,代数式x2﹣2的值为﹣2,不符合题意;
故选:C.
6.【答案】C
【解答】解:A、4+5ab≠9ab,故此选项错误;
B、6xy﹣y,无法计算,故此选项错误;
C、3ab﹣3ba=0,故此选项正确;
D、12x3+4x4,无法计算,故此选项错误;
故选:C.
7.【答案】B
【解答】解:A和B都是三次多项式,则A+B一定是次数不高于3的整式,
故选:B.
8.【答案】D
【解答】解:A.﹣ab3与b3a,字母相同,字母的次数也相同,故是同类项,不符合题意;
B.12与0是常数,故是同类项,不符合题意;
C.2xyz与﹣zyx,字母相同,字母的次数也相同,故是同类项,不符合题意;
D.3x2y与﹣6xy2,字母相同,字母的次数不相同,故不是同类项,符合题意;
故选:D.
9.【答案】B
【解答】解:当a+4b,
9(a+2b)﹣2(2a﹣b)
=5a+20b
=5(a+4b)
=5×()
=﹣1,
故选:B.
10.【答案】C
【解答】解:∵x2﹣2x=2y﹣y2,xy,
∴x2﹣2x+y2﹣2y=0,2xy=1,
∴x2+2xy+y2﹣2(x+y)+2019=x2﹣2x+y2﹣2y+1+2019=2020,
故选:C.
11.【答案】B
【解答】解:A.2a与3b不是同类项,不能合并,此选项错误;
B.5a2b﹣2a2b=(5﹣2)a2b=3a2b,此选项正确;
C.5a﹣3a=(5﹣3)a=2a,此选项错误;
D.6a+a=(6+1)a=7a,此选项错误;
故选:B.
12.【答案】D
【解答】解:±±3,
∴输入的数是:
(﹣3+1)÷2
=﹣2÷2
=﹣1
(3+1)÷2
=4÷2
=2
故选:D.
13.【答案】B
【解答】解:m3n4﹣5m3n5+3是八次三项式,故项数是3,次数是8.
故选:B.
14.【答案】A
【解答】解:设S()2+()3+…+()2020,
则4S=1()2+()3+…+()2019,
4S﹣S=1﹣()2020,
3S=1﹣()2020,
S,
故选:A.
15.【答案】C
【解答】解:(1)a+(b﹣c)=a+b﹣c,故此题正确;
(2)a﹣(b+c)=a﹣b﹣c,故此题正确;
(3)a﹣(b﹣c)=a﹣b+c,故此题错误;
(4)a﹣(b﹣c)=a﹣b+c,故此题正确.
所以运算结果正确的个数为3个,
故选:C.
16.【答案】D
【解答】解:根据图形的变化可知:
一种长方形餐桌的四周可坐6人用餐,即4×1+2=6;
2种长方形餐桌的四周可坐6人用餐,即4×2+2=10;
3种长方形餐桌的四周可坐6人用餐,即4×3+2=14;
…
发现规律:
n种长方形餐桌的四周可坐6人用餐,即4n+2;
∴4n+2=78.
解得n=19.
所以需要19张餐桌拼在一起可坐78人用餐.
故选:D.
17.【答案】B
【解答】解:∵﹣x3y2与3y2xn是同类项,
∴n=3,
故选:B.
18.【答案】C
【解答】解:A、结果是3a,故本选项错误;
B、结果是3n,故本选项错误;
C、结果是﹣m,故本选项正确;
D、结果是2a,故本选项错误;
故选:C.
19.【答案】C
【解答】解:观察图形的变化可知:
奇数项:2、6、10、14…4n﹣2(n为正整数);
偶数项:﹣4、﹣8、﹣12、﹣16…﹣4n.
∵﹣2020是偶数项,
∴﹣4n=﹣2020,
∴n=505.
∵每四条射线为一组,OC为始边,
∴505÷4=126…1.
∴标记为“﹣2020”的点在射线OC上.
故选:C.
二.填空题(共1小题)
20.【答案】70.
【解答】解:要使a+b+c+d的值最大,
此时d>1,
要使a+b+c+d有最大值,且a+b2+c3+d4=90,
∴b,c,d尽可能取最小,
∴d=2,c=1,b=3,
a=90﹣(b2+c3+d4)=90﹣(9+1+16)=64,
故a+b+c+d的最大值是64+3+2+1=70.
故答案为:70.
三.解答题(共20小题)
21.【答案】见试题解答内容
【解答】解:(1)当x=1时,3x+1=4,
故答案为:4;
(2)当x=4时,第1次结果为:2,第2次结果为1,第3次结果为3x+1=4;
故答案为:4;
(3)当x=3时,
第1次结果为:3x+1=10,第2次结果为5,第3次结果为3x+1=16;第4次结果为8,
第5次结果为4,第6次结果为2,第7次结果为1,
第8次结果为3x+1=4,……
∵(20﹣4)÷3=5……1,
∴第20次运算的结果为4.
∴有7个不同的值,
故答案为:7,4.
22.【答案】见试题解答内容
【解答】解;(1)由图形规律可得,答案为5,7;
(2)∵5﹣3=7﹣5=2,
∴三角形内的点每增加1个,最多可以剪得的三角形增加2个;
∵三角形内点的个数为1时,最多剪出的小三角形个数3=2×1+1,
三角形内点的个数为2时,最多剪出的小三角形个数5=2×2+1,
三角形内点的个数为3时,7最多剪出的小三角形个数7=2×3+1,
∴三角形内点的个数为n时,最多剪出的小三角形个数2n+1.
故答案为2,(2n+1);
(3)
加数的个数
和
1+3
22
1+3+5
32
1+3+5+7
42
…
…
1+3+5+7+…+(2n﹣1)
n2
证明:∵S=1+3+5+7+…+(2n﹣5)+(2n﹣3)+(2n﹣1)
∴S=(2n﹣1)+(2n﹣3)+(2n﹣5)+…+7+5+3+1
∴S+S=2n?n=2n2
2S=2n2
S=n2
23.【答案】见试题解答内容
【解答】解:(1)∵3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2=(3﹣6+2)(a﹣b)2=﹣(a﹣b)2;
故答案为:﹣(a﹣b)2;
(2)∵x2﹣2y=4,
∴原式=3(x2﹣2y)﹣21=12﹣21=﹣9;
(3)∵a﹣2b=3①,2b﹣c=﹣5②,c﹣d=10③,
由①+②可得a﹣c=﹣2,
由②+③可得2b﹣d=5,
∴原式=﹣2+5﹣(﹣5)=8.
24.【答案】见试题解答内容
【解答】解:原式=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2,
当a=﹣2,b=3时,原式=36+18=54.
25.【答案】见试题解答内容
【解答】解:(1)(﹣2)※3=(﹣2)2+2×(﹣2)×3=4﹣12=﹣8;
(2)∵1※x=3,
∴12+2x=3,
∴2x=3﹣1,
∴x=1;
(3)﹣2※x=﹣2+x,
(﹣2)2+2×(﹣2)x=﹣2+x,
4﹣4x=﹣2+x,
﹣4x﹣x=﹣2﹣4,
﹣5x=﹣6,
x.
26.【答案】见试题解答内容
【解答】解:原式=2x2y﹣[5xy2+2x2y﹣6xy2+2]
=2x2y﹣5xy2﹣2x2y+6xy2﹣2
=xy2﹣2,
由(x﹣2)2+|y+1|=0,得到x=2,y=﹣1,
则原式=2×(﹣1)2﹣2=2﹣2=0.
27.【答案】见试题解答内容
【解答】解:(1)原式=﹣256﹣()×0﹣1
=﹣256﹣1
=﹣257;
(2)原式=18﹣6×()×()
=18
;
(3)原式=2a﹣5b+a+b
=3a﹣4b;
(4))﹣[2m﹣3(m﹣n+1)﹣2]﹣1
=﹣2m+3(m﹣n+1)+2﹣1
=﹣2m+3m﹣3n+3+2﹣1
=m﹣3n+4.
28.【答案】见试题解答内容
【解答】解:(1)设所求数为x,
由已知等式可得,2x﹣5=5x,
∴x,
故答案为,;
(2)①∵2x﹣y=xy,
∴2x=y(1+x),
当x=﹣1时,等式不成立,
当y=2时,2x=2+2x,等式不成立,
∴x≠﹣1,y≠2;
②y2,
当1+x=±2时,x=1或x=﹣3,y=1或y=3;
当1+x=±1时,x=0或x=﹣2,y=0或y=4.
29.【答案】见试题解答内容
【解答】解:(1)输入数对(1,﹣2),即a=1,b=﹣2,
W=[|a﹣b|+(a+b)]1.
故答案为:1.
(2)当a=m,b=﹣n时,W1=[|a﹣b|+(a+b)][|m+n|+(m﹣n)].
当a=﹣n,b=m时,W2=[|a﹣b|+(a+b)][|﹣n﹣m|+(m﹣n)][|m+n|+(m﹣n)].
即W1=W2;
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W.
①当x≥3时,W[x﹣2﹣(x﹣3)+(x﹣2)+(x﹣3)](2x﹣4)=26
解得x=28,
则a+b=x﹣2+x﹣3=51;
②当2≤x<3时,W[|x﹣2﹣(3﹣x)|+(x﹣2)﹣(x﹣3)]=26
x=28或﹣23(均不合题意舍去);
③当x<2时,W[|2﹣x﹣(3﹣x)|﹣(x﹣2)﹣(x﹣3)](﹣4x+10)=26,
解得x=﹣23,
则a+b=51.
综上所述,a+b的值为51.
30.【答案】见试题解答内容
【解答】解:(1)原式=﹣2÷(﹣2)=1;
(2)原式(﹣36)(﹣36)(﹣36),
=18﹣27+8,
=﹣1;
(3)原式=﹣1()×(2﹣9),
=﹣1()×(﹣7),
=﹣1,
;
(4)原式=2a2﹣2ab+2a2﹣3ab+4ab,
=4a2﹣ab.
31.【答案】见试题解答内容
【解答】解:原式=3x2+2xy﹣3y2﹣2x2﹣2xy+2y2=x2﹣y2,
当x=﹣1,y=2时,原式=1﹣4=﹣3.
32.【答案】见试题解答内容
【解答】解:(1)原式=2x﹣5y;
(2)原式=2x2﹣4x﹣2x2﹣3x=﹣7x.
33.【答案】见试题解答内容
【解答】解:(1)由题意可得,
数轴上点P表示的数为:1.5,
故答案为:﹣1.5;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为:﹣1.5+2.5=1或﹣1.5﹣2.5=﹣4,
故答案为:1或﹣4;
(3)设点B表示的数为b,
则﹣1.5,得b=﹣3﹣m,
故答案为:﹣3﹣m.
34.【答案】见试题解答内容
【解答】解:原式=6x2y+2xy2﹣6x2y+3xy﹣2xy2+1=3xy+1,
当x,y=1时,原式=1+1=2.
35.【答案】见试题解答内容
【解答】解:(1)原式=5﹣9÷(﹣3)=5+3=8;
(2)原式=﹣1﹣2+12=9;
(3)原式=﹣5m﹣8n;
(4)原式=x2+4xy﹣(xy﹣x2)﹣2xy
=x2+4xy﹣xy+x2﹣2xy
=2x2+xy.
36.【答案】见试题解答内容
【解答】解:(1)原式=2x2+x﹣6;
(2)原式=2a2﹣4a+1+3a2﹣2a+5,
=5a2﹣6a+6.
37.【答案】见试题解答内容
【解答】解:原式=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2,
由|a+2|+(b﹣3)2=0,得到a+2=0,b﹣3=0,
解得:a=﹣2,b=3,
则原式=36+18=54.
38.【答案】见试题解答内容
【解答】解:原式=3a2+b2﹣12a2+2b2=﹣9a2+3b2,
当a=﹣2,b=3时,原式=﹣36+27=﹣9.
39.【答案】见试题解答内容
【解答】解:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b)=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2=ab(3a﹣b),
∵(a﹣1)2与|b|互为相反数,
∴(a﹣1)2+|b|=0
∴a=2,b,
∴原式=﹣(6).
40.【答案】见试题解答内容
【解答】解:(1)由题意得:(3a+2b)﹣(2a﹣b)=3a+2b﹣2a+b=a+3b,
答:C、D两站的距离为(a+3b)千米.
(2)(a+b)+2(2a﹣b)+(3a+2b)=a+b+4a﹣2b+3a+2b=8a+b
答:小明从A站到D站乘车路程共计(8a+b)千米.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
