4.6.3 余角和补角-华东师大版七年级数学上册的课件(共14张ppt)
文档属性
| 名称 | 4.6.3 余角和补角-华东师大版七年级数学上册的课件(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 07:34:06 | ||
图片预览






文档简介
(共14张PPT)
4.6.3
余角和补角
学习目标:
掌握余角和补角的定义,会求一个角的余角和补角;
理解并运用余角和补角的相关性质
1
问题引入
计算:
(1)48°+42°=
(2)30°20′+59°40′=
(3)37°+143°=
(4)120°30′+59°30′=
90°
90°
180°
180°
1
复习引入
2
初窥门径
两个角的和等于90°,就说这两个角互为余角,简称互余。
余角
如:∠1+∠2=90°,则∠1是∠2的余角,∠2也是∠1的余角
若已知∠1和∠2互余,能得到什么结论?
若∠1和∠2互余,则∠1+∠2=90°
O
1
2
2
初窥门径
余角
判断下列说法是否正确:
(1)∠1是余角;
(2)∠1=90°,∠2=90°,则∠1和∠2互余;
(3)∠1=40°,∠2=50°,则∠1与∠2互余。
错
错
对
2
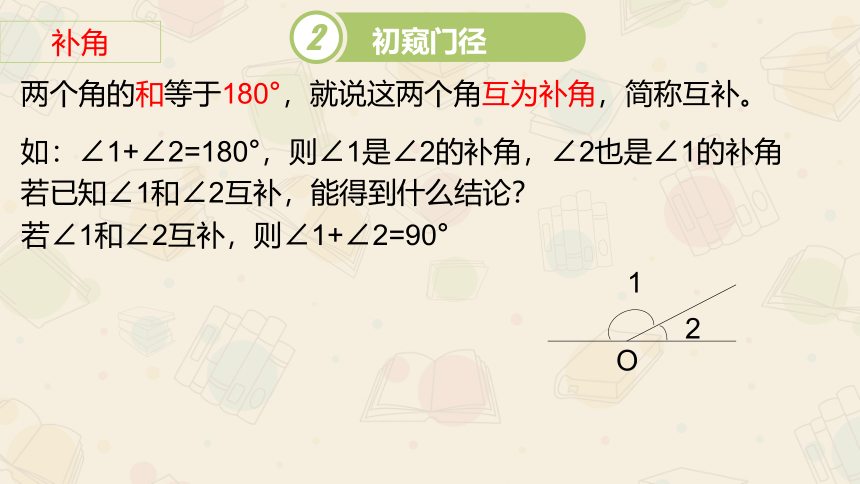
初窥门径
补角
两个角的和等于180°,就说这两个角互为补角,简称互补。
O
1
2
如:∠1+∠2=180°,则∠1是∠2的补角,∠2也是∠1的补角
若已知∠1和∠2互补,能得到什么结论?
若∠1和∠2互补,则∠1+∠2=90°
2
初窥门径
余角和补角
小试牛刀:说出图中互余和互补的角。
E
A
B
F
D
解:互余的角:∠DEF和∠FEB
互补的角:∠DEA和∠DEB
2
初窥门径
余角和补角
试一试:
∠α
∠α的余角
∠α的补角
5°
62°23′
135°
85°
175°
117°37′
27°37′
无
45°
1
复习引入
2
初窥门径
余角的性质
如图,∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,那么∠2与∠4相等吗?为什么?你能用一句话概括这一规律吗?
1
2
3
4
∵∠1与∠2互余,∠3与∠4互余
∴
∠2
=
90°─∠1,∠4
=
90°─∠3
∵
∠1=∠3
∴
∠2
=∠4
答:∠2
与∠4相等。理由如下:
余角性质:同角(等角)的余角相等
2
初窥门径
补角的性质
2
1
4
3
∵
∠1
与∠2互补
,∠3与∠4互补
∴
∠1
+∠2=1800
,
∠3+∠4=180°
∴
∠2=1800-∠1
,∠4=180°-∠3
又∵
∠1=∠3
∴
∠2=∠4
如图,∠1
与∠2互补,∠3
与∠4互补
,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
解:
补角性质:同角(等角)的补角相等
2
初窥门径
性质应用:
如图,∠AOD=∠COB=90°,∠1=46°,求∠2和∠3。
O
A
B
D
C
2
1
3
解:由已知,可得
∠2+∠1=90°,∠1+∠3=90°
根据同角的余角相等,得
∠2=∠3=90°-∠1=90°-46°=44°
挑战升级:
如图,EF、EG分别是∠AEB和∠BEC的平分线,求∠GEF的度数,并写出∠BEF的余角。
E
A
G
C
B
F
?
2
初窥门径
点到直线的距离
A
B
C
D
O
试一试:
如图,点A到直线CD的距离是(
)
A.直线AO
B.线段AO
C.线段AO的长度
D.线段AB的长度
C
注意事项:点到直线的距离是垂线段的长度,不是垂线段
3
练习巩固
3
课堂小结
作业:同步练习册5.1(一)
谈谈本节课你有什么收获?
1.垂直的定义
2.垂线的性质
3.点到直线的距离
有什么注意事项?
点到直线的距离是垂线段的长度,不是垂线段
4.6.3
余角和补角
学习目标:
掌握余角和补角的定义,会求一个角的余角和补角;
理解并运用余角和补角的相关性质
1
问题引入
计算:
(1)48°+42°=
(2)30°20′+59°40′=
(3)37°+143°=
(4)120°30′+59°30′=
90°
90°
180°
180°
1
复习引入
2
初窥门径
两个角的和等于90°,就说这两个角互为余角,简称互余。
余角
如:∠1+∠2=90°,则∠1是∠2的余角,∠2也是∠1的余角
若已知∠1和∠2互余,能得到什么结论?
若∠1和∠2互余,则∠1+∠2=90°
O
1
2
2
初窥门径
余角
判断下列说法是否正确:
(1)∠1是余角;
(2)∠1=90°,∠2=90°,则∠1和∠2互余;
(3)∠1=40°,∠2=50°,则∠1与∠2互余。
错
错
对
2
初窥门径
补角
两个角的和等于180°,就说这两个角互为补角,简称互补。
O
1
2
如:∠1+∠2=180°,则∠1是∠2的补角,∠2也是∠1的补角
若已知∠1和∠2互补,能得到什么结论?
若∠1和∠2互补,则∠1+∠2=90°
2
初窥门径
余角和补角
小试牛刀:说出图中互余和互补的角。
E
A
B
F
D
解:互余的角:∠DEF和∠FEB
互补的角:∠DEA和∠DEB
2
初窥门径
余角和补角
试一试:
∠α
∠α的余角
∠α的补角
5°
62°23′
135°
85°
175°
117°37′
27°37′
无
45°
1
复习引入
2
初窥门径
余角的性质
如图,∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,那么∠2与∠4相等吗?为什么?你能用一句话概括这一规律吗?
1
2
3
4
∵∠1与∠2互余,∠3与∠4互余
∴
∠2
=
90°─∠1,∠4
=
90°─∠3
∵
∠1=∠3
∴
∠2
=∠4
答:∠2
与∠4相等。理由如下:
余角性质:同角(等角)的余角相等
2
初窥门径
补角的性质
2
1
4
3
∵
∠1
与∠2互补
,∠3与∠4互补
∴
∠1
+∠2=1800
,
∠3+∠4=180°
∴
∠2=1800-∠1
,∠4=180°-∠3
又∵
∠1=∠3
∴
∠2=∠4
如图,∠1
与∠2互补,∠3
与∠4互补
,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
解:
补角性质:同角(等角)的补角相等
2
初窥门径
性质应用:
如图,∠AOD=∠COB=90°,∠1=46°,求∠2和∠3。
O
A
B
D
C
2
1
3
解:由已知,可得
∠2+∠1=90°,∠1+∠3=90°
根据同角的余角相等,得
∠2=∠3=90°-∠1=90°-46°=44°
挑战升级:
如图,EF、EG分别是∠AEB和∠BEC的平分线,求∠GEF的度数,并写出∠BEF的余角。
E
A
G
C
B
F
?
2
初窥门径
点到直线的距离
A
B
C
D
O
试一试:
如图,点A到直线CD的距离是(
)
A.直线AO
B.线段AO
C.线段AO的长度
D.线段AB的长度
C
注意事项:点到直线的距离是垂线段的长度,不是垂线段
3
练习巩固
3
课堂小结
作业:同步练习册5.1(一)
谈谈本节课你有什么收获?
1.垂直的定义
2.垂线的性质
3.点到直线的距离
有什么注意事项?
点到直线的距离是垂线段的长度,不是垂线段
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
