北师大版九年级数学上册6.1 反比例函数 课件(共22张ppt)
文档属性
| 名称 | 北师大版九年级数学上册6.1 反比例函数 课件(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
九上北师大版
第六章
反比例函数
6.1
反比例函数
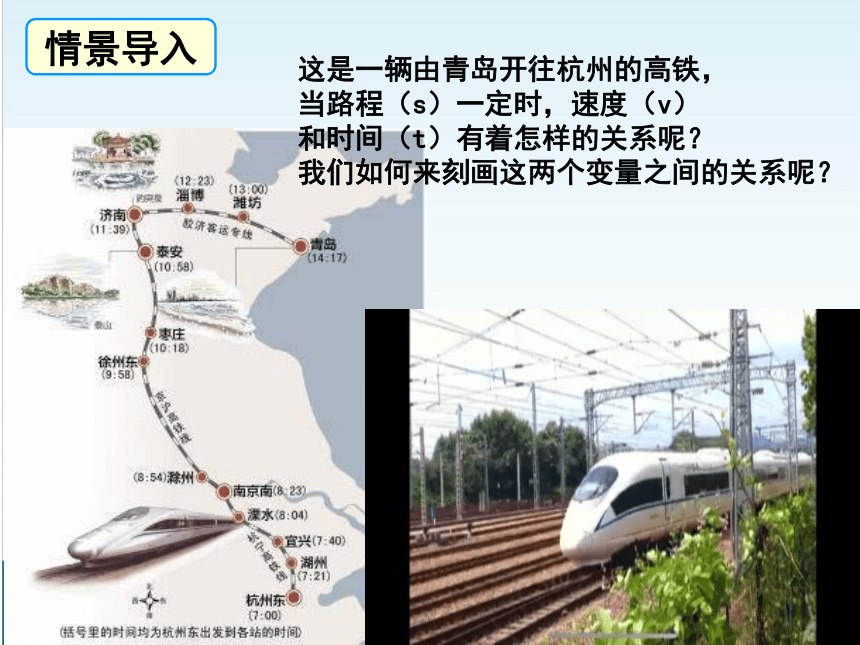
情景导入
这是一辆由青岛开往杭州的高铁,
当路程(s)一定时,速度(v)
和时间(t)有着怎样的关系呢?
我们如何来刻画这两个变量之间的关系呢?
本章将研究反比例函数,与一次函数一样,反比例函数也是描述很多现实问题中变量之间关系的重要数学模型。那什么是反比例函数?它对应的图象有什么特征?用反比例函数可以解决现实生活中的哪些问题?
让我们一起来走进函数世界吧!
第六章
反比例函数
目标明确
“函数”知多少
学而时习之不亦说乎?
函数定义:
一、什么是函数?
一般地,在某个变化过程中,有_____
变量_____,并且对于变量x的每一个值,
变量y都有______
的值与它相对应,那么我们称__________,其中x叫______,y叫______.
两个
x和y
y是x的函数
自变量
因变量
唯一
温故知新
二、函数的表示方法有哪些?
关系式法
列表法
图象法
函数的表示方法一般有:
温故知新
正比例函数的表达式为
(其中k,b为常数且k≠0)
y=kx+b
一次函数的表达式为
(其中k≠0的常数
)
y=kx
三、你学过哪些函数?它们的一般形式是什么?
正比例函数是特殊的一次函数
温故知新
问题1:情景导入中青杭高速铁路全长约为1092km,列车沿青杭高速铁路从青岛驶往杭州,列车行完全程所需的时间t
(h)与行驶的平均速度v(
km
/h)之间有怎样的关系?变量t是v的函数吗?为什么?
变量t
与v之间的关系可以表示成:
探索新知
探索新知
探索新知
sy=30
问题2:面团体积为
30
,总长度y(m),和横截面积s(
)
的函数关系?
变量y是s的函数吗?为什么?
舞台的灯光效果
探索新知
欧姆定律
问题3:我们知道,导体中的电流I,与导体的电阻R、导体两端的电压之间满足关系式U=IR,当U=220V时,
(1)请用含有R的代数式表示I.
(2)利用写出的关系式完成下表:
R/Ω
20
40
60
80
100
I/A
11
5.5
3.67
2.75
2.2
当R
越来越大时,I
怎样变化?当R
越来越小呢?
(3)变量I
是R的函数吗?为什么?
I
随着R的增大而变小,随着R
的减小而变大.
探索新知
一般地,如果两个变量y与x的关系可以表示成
的形式,那么称
y
是
x
的反比例函数.
(k为常数,
k≠0)
其中x是自变量不能为0,常数k(k≠0)称为反比例函数的反比例系数.
概念归纳
想一想:反比例函数还可以写成哪些形式?
xy=k
y=kx-1
(k≠0)
上述三个情景中出现的
、
、
有什么共
同特征?
1、在下列函数表达式中,哪些式子表示y是x的反比例函数?比例系数k值是多少?
(1)y=
5
x
(2)y=-
0.4
x
(3)y=
—
(4)xy=2
(5)y=
x
2
(6)
y=
(7)
y=x-1
(8)y=
1
x
-
1
2
1+x
5x
-2
(9)
y=
x
a
(10)
y=
x
a2+1
应用新知--小试“牛刀”
应用新知--“才华”显露
3、已知函数y=3xm-7是反比例函数,则
m
=
___
.
4、当m
=
___
时,函数
是x的反比例函数.
1、一个矩形的面积是20cm2,相邻的两条边长为xcm和y
cm,那么变量y是x的函数吗?是反比例函数吗?为什么?
2、如果函数
为反比例函数,则m的取值范围
_____
6
1
5、当m取什么值时,函数
是x的反比例函数?
m=-2
(1).写出这个反比例函数的表达式;
6、y是x的反比例函数,下表给出了x与y的一些值
x
-2
-1
1
3
Y
2
-1
解:∵
y是x的反比例函数,
(2).根据函数表达式完成上表.
把x=-1,y=2代入上式得:
-3
1
4
-4
-2
2
应用新知--“情系”待定系数法
课堂总结--分享你的收获
表达式
数学方法
反比例函数
建模思想
xy=k
y=kx-1
应用
欧姆定律,路程问题
类比
(k≠0)
(k≠0)
(k≠0)
无论是高铁情景、拉面情景、还是灯光情景等等,我们都不难发现函数来源于生活而又应用于生活。希望同学们做生活的有心人,发现数学,用好数学,让我们的生活更加美好!为实现中华民族的伟大复兴贡献自己的一份力量!
1、如果函数
为反比例函数,则k=_______
此时函数的解析式为______
y=
k
X2k+3
2、已知y与x2
成反比例,并且当x=3时y=4.
⑴
写出y和x之间的函数关系式;
⑵
求x=1.5时y的值。
当堂检测--更上一层楼
作业
内容
必做题
习题6.1:1-4题
选做题
再举出两个反比例函数的实例
布置作业
谢谢聆听
青岛西海岸新区育英初级中学
2020.11.5
九上北师大版
第六章
反比例函数
6.1
反比例函数
情景导入
这是一辆由青岛开往杭州的高铁,
当路程(s)一定时,速度(v)
和时间(t)有着怎样的关系呢?
我们如何来刻画这两个变量之间的关系呢?
本章将研究反比例函数,与一次函数一样,反比例函数也是描述很多现实问题中变量之间关系的重要数学模型。那什么是反比例函数?它对应的图象有什么特征?用反比例函数可以解决现实生活中的哪些问题?
让我们一起来走进函数世界吧!
第六章
反比例函数
目标明确
“函数”知多少
学而时习之不亦说乎?
函数定义:
一、什么是函数?
一般地,在某个变化过程中,有_____
变量_____,并且对于变量x的每一个值,
变量y都有______
的值与它相对应,那么我们称__________,其中x叫______,y叫______.
两个
x和y
y是x的函数
自变量
因变量
唯一
温故知新
二、函数的表示方法有哪些?
关系式法
列表法
图象法
函数的表示方法一般有:
温故知新
正比例函数的表达式为
(其中k,b为常数且k≠0)
y=kx+b
一次函数的表达式为
(其中k≠0的常数
)
y=kx
三、你学过哪些函数?它们的一般形式是什么?
正比例函数是特殊的一次函数
温故知新
问题1:情景导入中青杭高速铁路全长约为1092km,列车沿青杭高速铁路从青岛驶往杭州,列车行完全程所需的时间t
(h)与行驶的平均速度v(
km
/h)之间有怎样的关系?变量t是v的函数吗?为什么?
变量t
与v之间的关系可以表示成:
探索新知
探索新知
探索新知
sy=30
问题2:面团体积为
30
,总长度y(m),和横截面积s(
)
的函数关系?
变量y是s的函数吗?为什么?
舞台的灯光效果
探索新知
欧姆定律
问题3:我们知道,导体中的电流I,与导体的电阻R、导体两端的电压之间满足关系式U=IR,当U=220V时,
(1)请用含有R的代数式表示I.
(2)利用写出的关系式完成下表:
R/Ω
20
40
60
80
100
I/A
11
5.5
3.67
2.75
2.2
当R
越来越大时,I
怎样变化?当R
越来越小呢?
(3)变量I
是R的函数吗?为什么?
I
随着R的增大而变小,随着R
的减小而变大.
探索新知
一般地,如果两个变量y与x的关系可以表示成
的形式,那么称
y
是
x
的反比例函数.
(k为常数,
k≠0)
其中x是自变量不能为0,常数k(k≠0)称为反比例函数的反比例系数.
概念归纳
想一想:反比例函数还可以写成哪些形式?
xy=k
y=kx-1
(k≠0)
上述三个情景中出现的
、
、
有什么共
同特征?
1、在下列函数表达式中,哪些式子表示y是x的反比例函数?比例系数k值是多少?
(1)y=
5
x
(2)y=-
0.4
x
(3)y=
—
(4)xy=2
(5)y=
x
2
(6)
y=
(7)
y=x-1
(8)y=
1
x
-
1
2
1+x
5x
-2
(9)
y=
x
a
(10)
y=
x
a2+1
应用新知--小试“牛刀”
应用新知--“才华”显露
3、已知函数y=3xm-7是反比例函数,则
m
=
___
.
4、当m
=
___
时,函数
是x的反比例函数.
1、一个矩形的面积是20cm2,相邻的两条边长为xcm和y
cm,那么变量y是x的函数吗?是反比例函数吗?为什么?
2、如果函数
为反比例函数,则m的取值范围
_____
6
1
5、当m取什么值时,函数
是x的反比例函数?
m=-2
(1).写出这个反比例函数的表达式;
6、y是x的反比例函数,下表给出了x与y的一些值
x
-2
-1
1
3
Y
2
-1
解:∵
y是x的反比例函数,
(2).根据函数表达式完成上表.
把x=-1,y=2代入上式得:
-3
1
4
-4
-2
2
应用新知--“情系”待定系数法
课堂总结--分享你的收获
表达式
数学方法
反比例函数
建模思想
xy=k
y=kx-1
应用
欧姆定律,路程问题
类比
(k≠0)
(k≠0)
(k≠0)
无论是高铁情景、拉面情景、还是灯光情景等等,我们都不难发现函数来源于生活而又应用于生活。希望同学们做生活的有心人,发现数学,用好数学,让我们的生活更加美好!为实现中华民族的伟大复兴贡献自己的一份力量!
1、如果函数
为反比例函数,则k=_______
此时函数的解析式为______
y=
k
X2k+3
2、已知y与x2
成反比例,并且当x=3时y=4.
⑴
写出y和x之间的函数关系式;
⑵
求x=1.5时y的值。
当堂检测--更上一层楼
作业
内容
必做题
习题6.1:1-4题
选做题
再举出两个反比例函数的实例
布置作业
谢谢聆听
青岛西海岸新区育英初级中学
2020.11.5
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
