北师大版八年级数学上册《1.1 探索勾股定理》 同步练习(word版含答案)
文档属性
| 名称 | 北师大版八年级数学上册《1.1 探索勾股定理》 同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 299.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 13:05:34 | ||
图片预览



文档简介
1.1
探索勾股定理
一.选择题
1.如图,△ABC中,∠ACB=90°,分别以三边为底向形外作等腰直角三角形,它们的面积依次为S1、S2、S3,则下列关系式正确的是( )
A.S1>S2+S3
B.S1<S2+S3
C.S1=S2+S3
D.S12=S22+S32
2.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A.AB=
B.∠BAC=90°
C.S△ABC=10
D.点A到直线BC的距离是2
3.在Rt△ABC中,∠ACB=90°,BC=6,AC=8,则Rt△ABC的斜边AB上的高CD的长是( )
A.
B.
C.9
D.6
4.如图,分别以直角△ABC的三边AB.BC、CA为直径向外作半圆,设直线AB左边阴影部分的面积为S1,右边阴影部分的面积为S2,则( )
A.S1>S2
B.S1<S2
C.S1=S2
D.S1、S2大小不确定
5.如图:三个正方形和一个直角三角形,图形A的面积是( )
A.225
B.144
C.81
D.无法确定
6.若直角三角形的两直角边长分别为5cm,12cm,则斜边上的高为( )
A.cm
B.cm
C.13cm
D.cm
7.若一个直角三角形的两直角边的长为12和5,则第三边的长为( )
A.13或
B.13或15
C.13
D.15
8.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A.
B.
C.
D.
9.以直角三角形三边作三个正方形,面积如图所示,则正方形A的面积为( )
A.4
B.6
C.8
D.10
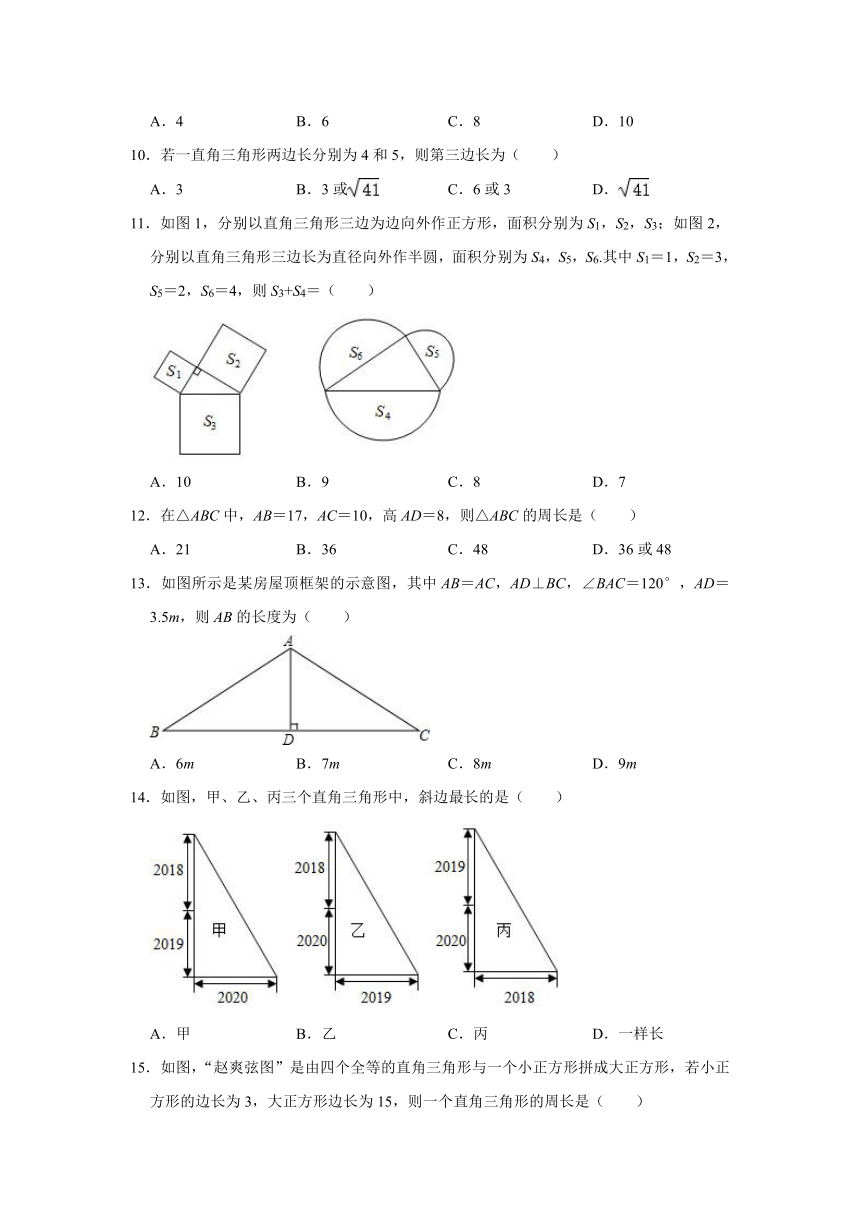
10.若一直角三角形两边长分别为4和5,则第三边长为( )
A.3
B.3或
C.6或3
D.
11.如图1,分别以直角三角形三边为边向外作正方形,面积分别为S1,S2,S3;如图2,分别以直角三角形三边长为直径向外作半圆,面积分别为S4,S5,S6.其中S1=1,S2=3,S5=2,S6=4,则S3+S4=( )
A.10
B.9
C.8
D.7
12.在△ABC中,AB=17,AC=10,高AD=8,则△ABC的周长是( )
A.21
B.36
C.48
D.36或48
13.如图所示是某房屋顶框架的示意图,其中AB=AC,AD⊥BC,∠BAC=120°,AD=3.5m,则AB的长度为( )
A.6m
B.7m
C.8m
D.9m
14.如图,甲、乙、丙三个直角三角形中,斜边最长的是( )
A.甲
B.乙
C.丙
D.一样长
15.如图,“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成大正方形,若小正方形的边长为3,大正方形边长为15,则一个直角三角形的周长是( )
A.45
B.36
C.25
D.18
二.填空题
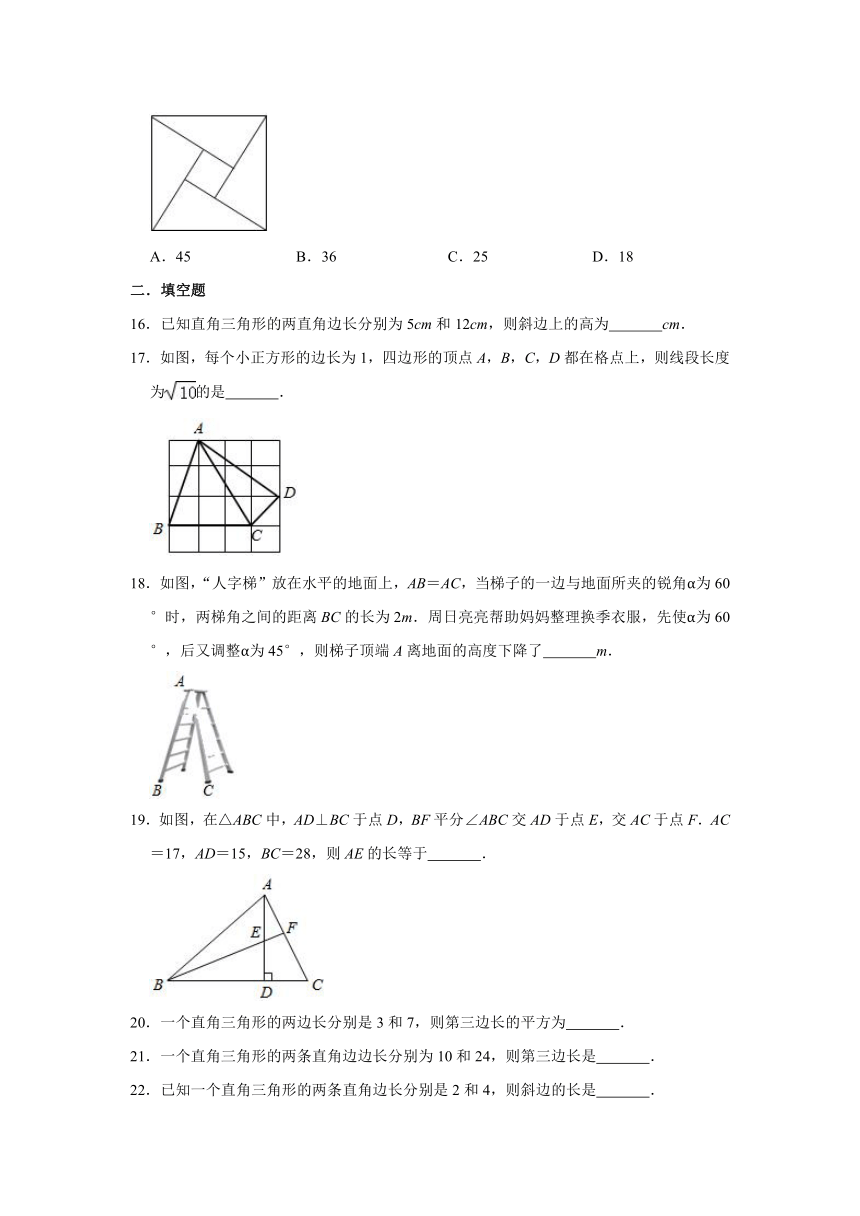
16.已知直角三角形的两直角边长分别为5cm和12cm,则斜边上的高为
cm.
17.如图,每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则线段长度为的是
.
18.如图,“人字梯”放在水平的地面上,AB=AC,当梯子的一边与地面所夹的锐角α为60°时,两梯角之间的距离BC的长为2m.周日亮亮帮助妈妈整理换季衣服,先使α为60°,后又调整α为45°,则梯子顶端A离地面的高度下降了
m.
19.如图,在△ABC中,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F.AC=17,AD=15,BC=28,则AE的长等于
.
20.一个直角三角形的两边长分别是3和7,则第三边长的平方为
.
21.一个直角三角形的两条直角边边长分别为10和24,则第三边长是
.
22.已知一个直角三角形的两条直角边长分别是2和4,则斜边的长是
.
23.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=4EF,则正方形ABCD的面积为
.
24.如图,由四个全等的直角三角形拼成的大正方形的面积为84,中间小正方形的面积为24,若直角三角形较长直角边为b,较短直角边为a,则a+b=
.
25.如图,在“赵爽弦图”中,△ABE、△BCF、△CDG和△DAH是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形.若AH=1,EF=1,则正方形ABCD的面积为
.
三.解答题
26.如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=3,AC=4.求AD的长.
27.等腰△ABC的面积为30,其中一边AB的长为10,另外两边为BC、AC,请你求出BC2,AC2的值.
28.如图,已知等腰△ABC,AB=AC,BC=,AB=5,求AC边上的高BD的长.
29.匀股定理被带为“几何明珠”,在数学的发展历程中占有举足轻重的地位.它是初中数学中的重要知识点之一,也是初中学生以后解决数学问题和实际问题中常常运用到的重要知识,因此学好勾股定理非常重要.学习数学“不仅要知其然,更要知其所以然”,所以,我们要学会勾股定理的各种证明方法.请你利用如图图形证明勾股定理:
已知:如图,四边形ABCD中,BD⊥CD,AE⊥BD于点E,且△ABE≌△BCD.求证:AB2=BE2+AE2.
30.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,也可以用面积法来证明,请将下面说理过程补充完整:
证明:连接DB,过点D作BC边上的高DF,交BC的延长线与点F,
则四边形DFCE为长方形,所以DF=EC=
.(用含字母的代数式表示)
因为S四边形ABCD=S△ACD+
=
+;
S四边形ABCD=S△ADB+
=
;
所以
;
所以
.
参考答案
一.选择题
1.解:如右图所示,
△ABC中,∠ACB=90°,分别以三边为底向形外作等腰直角三角形,
∴S1==,
同理可得,S2=,S3=,
∵∠ACB=90°,
∴a2+b2=c2,
∴S1=S2+S3,
故选:C.
2.解:由题意可得,
AB==2,故选项A正确;
AC==,
BC==5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,故选项B正确;
∴S△ABC==5,故选项C错误;
作AD⊥BC于点D,
则=5,
即=5,
解得,AD=2,
即点A到直线BC的距离是2,故选项D正确;
故选:C.
3.解:在Rt△ABC中,∠ACB=90°,BC=6,AC=8,
由勾股定理得,AB===10,
△ABC的面积=×BC×AC=×AB×CD,即=×6×8=×10×CD,
解得,CD=,
故选:B.
4.解:∵△ABC为Rt△,
∴AB2=AC2+BC2
又∵S=πR2,
∴S1=π()2,
S2=π()2+π()2=π()=π()2=S1,
∴S1=S2.
故选:C.
5.解:直角三角形的直角边的平方=225﹣144=81,
∴图形A的面积是81.
故选:C.
6.解:∵在直角三角形中,两直角边长分别为5cm,12cm,
∴斜边长2=52+122=169,
∴斜边长==13(cm).
设斜边上的高为h,则S=×5×12=×13h,
∴h==(cm).
故选:B.
7.解:∵一个直角三角形的两直角边的长为12和5,
∴第三边的长为=13.
故选:C.
8.解:由题意可得,
△ABC的面积是:3×4﹣=4,
∵BD是△ABC的高,AC==2,
∴=4,
解得,BD=,
故选:A.
9.解:如图,
在直角三角形BCD中,BC2+BD2=CD2,
∴BD2=10﹣4=6,
∴正方形A的面积为6,
故选:B.
10.解:①当4和5都是直角边时,则第三边是=;
②当5是斜边时,则第三边是=3.
故第三边长为3或.
故选:B.
11.解:如右图所示,
∵S1=a2,S2=b2,S3=c2,a2+b2=c2,
∴S1+S2=S3,
同理可得,S5+S6=S4,
∵S1=1,S2=3,S5=2,S6=4,
∴S3+S4=(1+3)+(2+4)=4+6=9,
故选:B.
12.解:分两种情况:
①如图1所示:
∵AD是BC边上的高,
∴∠ADB=∠ADC=90°,
∴BD===15,CD===6,
∴BC=BD+CD=15+6=21;
此时,△ABC的周长为:AB+BC+AC=17+10+21=48.
②如图2所示:
同①得:BD=15,CD=6,
∴BC=BD﹣CD=15﹣6=9;
此时,△ABC的周长为:AB+BC+AC=17+10+9=36.
综上所述:△ABC的周长为48或36.
故选:D.
13.解:∵在△ABC中,AB=AC,AD⊥BC,∠BAC=120°.
∴∠B=∠C=(180°﹣120°)÷2=30°,
∴∠BAD=∠BAC=60°;
在△ABC中,AD=3.5m,∠C=30°,
∴AB=2AD=7m.
故选:B.
14.解:由勾股定理可知甲、乙、丙三个直角三角形中,斜边的平方分别为:
甲:(2018+2019)2+20202;
乙:(2018+2020)2+20192;
丙:(2019+2020)2+20182.
∵(2018+2019)2+20202﹣[(2018+2020)2+20192]
=40372+20202﹣40382﹣20192
=(40372﹣40382)+(20202﹣20192)
=(4037+4038)(4037﹣4038)+(2020+2019)(2020﹣2019)
=﹣8075+4039
=﹣4036<0,
∴甲的斜边的小于乙的斜边;
∵(2018+2020)2+20192﹣[(2019+2020)2+20182]
=40382+20192﹣40392﹣20182
=(40382﹣40392)+(20192﹣20182)
=(4038+4039)(4038﹣4039)+(2019+2018)(2019﹣2018)
=﹣8077+4037
=﹣4040
<0,
∴乙的斜边的小于丙的斜边,
∴斜边最长的是丙.
故选:C.
15.解:设直角三角形两条直角边长分别为a和b,
由题意可知:中间小正方形的边长为:a﹣b=3,
根据大正方形的面积等于4个直角三角形的面积加上小正方形的面积可知:
225=4×ab+9,
所以2ab=216,
根据勾股定理,得a2+b2=152,
所以(a+b)2=a2+b2+2ab=225+216=441,
因为a+b>0,
所以a+b=21,
所以21+15=36.
所以一个直角三角形的周长是36.
故选:B.
二.填空题
16.解:∵直角三角形的两直角边长分别为5cm和12cm,
∴斜边长为:=13cm,
设斜边上的高为xcm,
则,
解得,x=,
即斜边上的高为cm,
故答案为:.
17.解:AB==,BC=3,CD==,AD==,
故长度为的线段是AB,
故答案是:AB.
18.解:如图1所示:
过点A作AD⊥BC于点D,
由题意可得:∠B=∠C=60°,
则△ABC是等边三角形,
故BC=AB=AC=2m,
则AD=2sin60°=m,
如图2所示:
过点A作AE⊥BC于点E,
由题意可得:∠B=∠C=60°,
则△ABC是等腰直角三角形,AC=AB,
则AE=BC=1m,
故梯子顶端离地面的高度AD下降了(﹣1)m.
故答案为:(﹣1).
19.解:∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵AD=15,AC=17,
∴DC=,
∵BC=28,
∴BD=28﹣8=20,
由勾股定理得:AB=,
过点E作EG⊥AB于G,
∵BF平分∠ABC,AD⊥BC,
∴EG=ED,
在Rt△BDE和Rt△BGE中,
∵,
∴Rt△BDE≌Rt△BGE(HL),
∴BG=BD=20,
∴AG=25﹣20=5,
设AE=x,则ED=15﹣x,
∴EG=15﹣x,
Rt△AGE中,x2=52+(15﹣x)2,
x=,
∴AE=.
故答案为:.
20.解:当第三边是斜边时,则有第三边的平方=32+72=58;
当第三边是直角边时,则有第三边的平方=72﹣32=40.
则第三边长的平方为58或40.
故答案是:58或40.
21.解:∵直角三角形的两条直角边分别为10和24,
∴第三边长==26.
故答案是:26.
22.解:由勾股定理得,斜边=,
故答案为:2.
23.解:设AM=2a.BM=b.则正方形ABCD的面积=4a2+b2,
由题意可知EF=(2a﹣b)﹣2(a﹣b)=2a﹣b﹣2a+2b=b,
∵AM=4EF,
∴2a=4b,
∴a=2b,
∵正方形EFGH的面积为2,
∴b2=2,
∴正方形ABCD的面积=4a2+b2=13b2=26,
故答案为:26.
24.解:根据题意得:c2=a2+b2=84,4×ab=84﹣24=60,即2ab=60,
则(a+b)2=a2+2ab+b2=84+60=144,
∴a+b=12,
故答案为:12.
25.解:∵△ADH≌△BAE,
∴BE=AH=1,
∵四边形EFGH都是正方形,
∴HE=EF=1,
∴AE=2,
在直角三角形ABE中,由勾股定理得到:AB2=AE2+BE2=22+12=5,
∴正方形ABCD的面积=AB2=5,
故答案为:5.
三.解答题
26.解:(1)∵∠ACD=90°,∠A=28°,
∴∠B=62°.
∵BD=BC,
∴∠BCD=∠BDC==59°.
∴∠ACD=90°﹣∠BCD=90°﹣59°=31°;
(2)∵∠ACB=90°,BC=3,AC=4,
由勾股定理得:AB===5,
∵AB=AD+BD,BD=BC=3,
∴AD=5﹣3=2.
27.解:过点C作CD⊥AB于D,
∵△ABC的面积为30,
∴×AB×CD=30,即×10×CD=30,
解得,CD=6,
如图1,当AB为底边,CA=CB时,
∵CD⊥AB,
∴AD=DB=AB=5,
∴AC2=BC2=52+62=61;
当AB为腰,且△ABC为锐角三角形,AB=AC=10时,如图2,
则AC2=AB2=100,
在Rt△ACD中,AD===8,
则BD=AB﹣AD=2,
∴BC2=CD2+BD2=40;
当AB为腰,且△ABC为钝角三角形,AB=BC=10时,如图3,
则BC2=AB2=100,
由勾股定理得,BD==8,
∴AD=AB+BD=18,
∴AC2=AD2+CD2=360,
综上所述,BC2,AC2的值分别为61,61或40,100或100,360.
28.解:过点A作AE⊥BC于点E,
∵等腰△ABC中,AB=AC=5,BC=,
∴BE=BC=,
∴AE==,
∴S△ABC=BC?AE=,
∵S△ABC=AC?BD,
∴BD==3.
29.解:连接AC,
∵△ABE≌△BCD,
∴AB=BC,AE=BD,BE=CD,∠BAE=∠CBD,
∵∠ABE+∠BAE=90°,
∴∠ABE+∠CBE=90°,
∴∠ABC=90°,
∴S四边形ABCD=S△ABD+S△BDC=BD?AE+BD?CD=AE?AE+AE?BE=BE2+BD?BE,
又∵S四边形ABCD=S△ABC+S△ADC=AB?BC+CD?DE=AB?AB+BE?DE=AB2+BE?DE,
∴BE2+AE?BE=AB2+BE?DE,
∴AB2=BE2+BD?BE﹣BE?DE,
∴AB2=BE2+(BD﹣DE)?BE,即AB2=BE2+AE2.
30.证明:连接DB,过点D作BC边上的高DF,交BC的延长线与点F,
则四边形DFCE为长方形,所以DF=EC=b﹣a.(用含字母的代数式表示)
因为S四边形ABCD=S△ACD+S△ABC=+;
S四边形ABCD=S△ADB+S△DCB=;
所以;
所以a2+b2=c2.
故答案为:b﹣a;S△ABC;;S△DCB;;;;a2+b2=c2.
探索勾股定理
一.选择题
1.如图,△ABC中,∠ACB=90°,分别以三边为底向形外作等腰直角三角形,它们的面积依次为S1、S2、S3,则下列关系式正确的是( )
A.S1>S2+S3
B.S1<S2+S3
C.S1=S2+S3
D.S12=S22+S32
2.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A.AB=
B.∠BAC=90°
C.S△ABC=10
D.点A到直线BC的距离是2
3.在Rt△ABC中,∠ACB=90°,BC=6,AC=8,则Rt△ABC的斜边AB上的高CD的长是( )
A.
B.
C.9
D.6
4.如图,分别以直角△ABC的三边AB.BC、CA为直径向外作半圆,设直线AB左边阴影部分的面积为S1,右边阴影部分的面积为S2,则( )
A.S1>S2
B.S1<S2
C.S1=S2
D.S1、S2大小不确定
5.如图:三个正方形和一个直角三角形,图形A的面积是( )
A.225
B.144
C.81
D.无法确定
6.若直角三角形的两直角边长分别为5cm,12cm,则斜边上的高为( )
A.cm
B.cm
C.13cm
D.cm
7.若一个直角三角形的两直角边的长为12和5,则第三边的长为( )
A.13或
B.13或15
C.13
D.15
8.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A.
B.
C.
D.
9.以直角三角形三边作三个正方形,面积如图所示,则正方形A的面积为( )
A.4
B.6
C.8
D.10
10.若一直角三角形两边长分别为4和5,则第三边长为( )
A.3
B.3或
C.6或3
D.
11.如图1,分别以直角三角形三边为边向外作正方形,面积分别为S1,S2,S3;如图2,分别以直角三角形三边长为直径向外作半圆,面积分别为S4,S5,S6.其中S1=1,S2=3,S5=2,S6=4,则S3+S4=( )
A.10
B.9
C.8
D.7
12.在△ABC中,AB=17,AC=10,高AD=8,则△ABC的周长是( )
A.21
B.36
C.48
D.36或48
13.如图所示是某房屋顶框架的示意图,其中AB=AC,AD⊥BC,∠BAC=120°,AD=3.5m,则AB的长度为( )
A.6m
B.7m
C.8m
D.9m
14.如图,甲、乙、丙三个直角三角形中,斜边最长的是( )
A.甲
B.乙
C.丙
D.一样长
15.如图,“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成大正方形,若小正方形的边长为3,大正方形边长为15,则一个直角三角形的周长是( )
A.45
B.36
C.25
D.18
二.填空题
16.已知直角三角形的两直角边长分别为5cm和12cm,则斜边上的高为
cm.
17.如图,每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则线段长度为的是
.
18.如图,“人字梯”放在水平的地面上,AB=AC,当梯子的一边与地面所夹的锐角α为60°时,两梯角之间的距离BC的长为2m.周日亮亮帮助妈妈整理换季衣服,先使α为60°,后又调整α为45°,则梯子顶端A离地面的高度下降了
m.
19.如图,在△ABC中,AD⊥BC于点D,BF平分∠ABC交AD于点E,交AC于点F.AC=17,AD=15,BC=28,则AE的长等于
.
20.一个直角三角形的两边长分别是3和7,则第三边长的平方为
.
21.一个直角三角形的两条直角边边长分别为10和24,则第三边长是
.
22.已知一个直角三角形的两条直角边长分别是2和4,则斜边的长是
.
23.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=4EF,则正方形ABCD的面积为
.
24.如图,由四个全等的直角三角形拼成的大正方形的面积为84,中间小正方形的面积为24,若直角三角形较长直角边为b,较短直角边为a,则a+b=
.
25.如图,在“赵爽弦图”中,△ABE、△BCF、△CDG和△DAH是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形.若AH=1,EF=1,则正方形ABCD的面积为
.
三.解答题
26.如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=3,AC=4.求AD的长.
27.等腰△ABC的面积为30,其中一边AB的长为10,另外两边为BC、AC,请你求出BC2,AC2的值.
28.如图,已知等腰△ABC,AB=AC,BC=,AB=5,求AC边上的高BD的长.
29.匀股定理被带为“几何明珠”,在数学的发展历程中占有举足轻重的地位.它是初中数学中的重要知识点之一,也是初中学生以后解决数学问题和实际问题中常常运用到的重要知识,因此学好勾股定理非常重要.学习数学“不仅要知其然,更要知其所以然”,所以,我们要学会勾股定理的各种证明方法.请你利用如图图形证明勾股定理:
已知:如图,四边形ABCD中,BD⊥CD,AE⊥BD于点E,且△ABE≌△BCD.求证:AB2=BE2+AE2.
30.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,也可以用面积法来证明,请将下面说理过程补充完整:
证明:连接DB,过点D作BC边上的高DF,交BC的延长线与点F,
则四边形DFCE为长方形,所以DF=EC=
.(用含字母的代数式表示)
因为S四边形ABCD=S△ACD+
=
+;
S四边形ABCD=S△ADB+
=
;
所以
;
所以
.
参考答案
一.选择题
1.解:如右图所示,
△ABC中,∠ACB=90°,分别以三边为底向形外作等腰直角三角形,
∴S1==,
同理可得,S2=,S3=,
∵∠ACB=90°,
∴a2+b2=c2,
∴S1=S2+S3,
故选:C.
2.解:由题意可得,
AB==2,故选项A正确;
AC==,
BC==5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,故选项B正确;
∴S△ABC==5,故选项C错误;
作AD⊥BC于点D,
则=5,
即=5,
解得,AD=2,
即点A到直线BC的距离是2,故选项D正确;
故选:C.
3.解:在Rt△ABC中,∠ACB=90°,BC=6,AC=8,
由勾股定理得,AB===10,
△ABC的面积=×BC×AC=×AB×CD,即=×6×8=×10×CD,
解得,CD=,
故选:B.
4.解:∵△ABC为Rt△,
∴AB2=AC2+BC2
又∵S=πR2,
∴S1=π()2,
S2=π()2+π()2=π()=π()2=S1,
∴S1=S2.
故选:C.
5.解:直角三角形的直角边的平方=225﹣144=81,
∴图形A的面积是81.
故选:C.
6.解:∵在直角三角形中,两直角边长分别为5cm,12cm,
∴斜边长2=52+122=169,
∴斜边长==13(cm).
设斜边上的高为h,则S=×5×12=×13h,
∴h==(cm).
故选:B.
7.解:∵一个直角三角形的两直角边的长为12和5,
∴第三边的长为=13.
故选:C.
8.解:由题意可得,
△ABC的面积是:3×4﹣=4,
∵BD是△ABC的高,AC==2,
∴=4,
解得,BD=,
故选:A.
9.解:如图,
在直角三角形BCD中,BC2+BD2=CD2,
∴BD2=10﹣4=6,
∴正方形A的面积为6,
故选:B.
10.解:①当4和5都是直角边时,则第三边是=;
②当5是斜边时,则第三边是=3.
故第三边长为3或.
故选:B.
11.解:如右图所示,
∵S1=a2,S2=b2,S3=c2,a2+b2=c2,
∴S1+S2=S3,
同理可得,S5+S6=S4,
∵S1=1,S2=3,S5=2,S6=4,
∴S3+S4=(1+3)+(2+4)=4+6=9,
故选:B.
12.解:分两种情况:
①如图1所示:
∵AD是BC边上的高,
∴∠ADB=∠ADC=90°,
∴BD===15,CD===6,
∴BC=BD+CD=15+6=21;
此时,△ABC的周长为:AB+BC+AC=17+10+21=48.
②如图2所示:
同①得:BD=15,CD=6,
∴BC=BD﹣CD=15﹣6=9;
此时,△ABC的周长为:AB+BC+AC=17+10+9=36.
综上所述:△ABC的周长为48或36.
故选:D.
13.解:∵在△ABC中,AB=AC,AD⊥BC,∠BAC=120°.
∴∠B=∠C=(180°﹣120°)÷2=30°,
∴∠BAD=∠BAC=60°;
在△ABC中,AD=3.5m,∠C=30°,
∴AB=2AD=7m.
故选:B.
14.解:由勾股定理可知甲、乙、丙三个直角三角形中,斜边的平方分别为:
甲:(2018+2019)2+20202;
乙:(2018+2020)2+20192;
丙:(2019+2020)2+20182.
∵(2018+2019)2+20202﹣[(2018+2020)2+20192]
=40372+20202﹣40382﹣20192
=(40372﹣40382)+(20202﹣20192)
=(4037+4038)(4037﹣4038)+(2020+2019)(2020﹣2019)
=﹣8075+4039
=﹣4036<0,
∴甲的斜边的小于乙的斜边;
∵(2018+2020)2+20192﹣[(2019+2020)2+20182]
=40382+20192﹣40392﹣20182
=(40382﹣40392)+(20192﹣20182)
=(4038+4039)(4038﹣4039)+(2019+2018)(2019﹣2018)
=﹣8077+4037
=﹣4040
<0,
∴乙的斜边的小于丙的斜边,
∴斜边最长的是丙.
故选:C.
15.解:设直角三角形两条直角边长分别为a和b,
由题意可知:中间小正方形的边长为:a﹣b=3,
根据大正方形的面积等于4个直角三角形的面积加上小正方形的面积可知:
225=4×ab+9,
所以2ab=216,
根据勾股定理,得a2+b2=152,
所以(a+b)2=a2+b2+2ab=225+216=441,
因为a+b>0,
所以a+b=21,
所以21+15=36.
所以一个直角三角形的周长是36.
故选:B.
二.填空题
16.解:∵直角三角形的两直角边长分别为5cm和12cm,
∴斜边长为:=13cm,
设斜边上的高为xcm,
则,
解得,x=,
即斜边上的高为cm,
故答案为:.
17.解:AB==,BC=3,CD==,AD==,
故长度为的线段是AB,
故答案是:AB.
18.解:如图1所示:
过点A作AD⊥BC于点D,
由题意可得:∠B=∠C=60°,
则△ABC是等边三角形,
故BC=AB=AC=2m,
则AD=2sin60°=m,
如图2所示:
过点A作AE⊥BC于点E,
由题意可得:∠B=∠C=60°,
则△ABC是等腰直角三角形,AC=AB,
则AE=BC=1m,
故梯子顶端离地面的高度AD下降了(﹣1)m.
故答案为:(﹣1).
19.解:∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵AD=15,AC=17,
∴DC=,
∵BC=28,
∴BD=28﹣8=20,
由勾股定理得:AB=,
过点E作EG⊥AB于G,
∵BF平分∠ABC,AD⊥BC,
∴EG=ED,
在Rt△BDE和Rt△BGE中,
∵,
∴Rt△BDE≌Rt△BGE(HL),
∴BG=BD=20,
∴AG=25﹣20=5,
设AE=x,则ED=15﹣x,
∴EG=15﹣x,
Rt△AGE中,x2=52+(15﹣x)2,
x=,
∴AE=.
故答案为:.
20.解:当第三边是斜边时,则有第三边的平方=32+72=58;
当第三边是直角边时,则有第三边的平方=72﹣32=40.
则第三边长的平方为58或40.
故答案是:58或40.
21.解:∵直角三角形的两条直角边分别为10和24,
∴第三边长==26.
故答案是:26.
22.解:由勾股定理得,斜边=,
故答案为:2.
23.解:设AM=2a.BM=b.则正方形ABCD的面积=4a2+b2,
由题意可知EF=(2a﹣b)﹣2(a﹣b)=2a﹣b﹣2a+2b=b,
∵AM=4EF,
∴2a=4b,
∴a=2b,
∵正方形EFGH的面积为2,
∴b2=2,
∴正方形ABCD的面积=4a2+b2=13b2=26,
故答案为:26.
24.解:根据题意得:c2=a2+b2=84,4×ab=84﹣24=60,即2ab=60,
则(a+b)2=a2+2ab+b2=84+60=144,
∴a+b=12,
故答案为:12.
25.解:∵△ADH≌△BAE,
∴BE=AH=1,
∵四边形EFGH都是正方形,
∴HE=EF=1,
∴AE=2,
在直角三角形ABE中,由勾股定理得到:AB2=AE2+BE2=22+12=5,
∴正方形ABCD的面积=AB2=5,
故答案为:5.
三.解答题
26.解:(1)∵∠ACD=90°,∠A=28°,
∴∠B=62°.
∵BD=BC,
∴∠BCD=∠BDC==59°.
∴∠ACD=90°﹣∠BCD=90°﹣59°=31°;
(2)∵∠ACB=90°,BC=3,AC=4,
由勾股定理得:AB===5,
∵AB=AD+BD,BD=BC=3,
∴AD=5﹣3=2.
27.解:过点C作CD⊥AB于D,
∵△ABC的面积为30,
∴×AB×CD=30,即×10×CD=30,
解得,CD=6,
如图1,当AB为底边,CA=CB时,
∵CD⊥AB,
∴AD=DB=AB=5,
∴AC2=BC2=52+62=61;
当AB为腰,且△ABC为锐角三角形,AB=AC=10时,如图2,
则AC2=AB2=100,
在Rt△ACD中,AD===8,
则BD=AB﹣AD=2,
∴BC2=CD2+BD2=40;
当AB为腰,且△ABC为钝角三角形,AB=BC=10时,如图3,
则BC2=AB2=100,
由勾股定理得,BD==8,
∴AD=AB+BD=18,
∴AC2=AD2+CD2=360,
综上所述,BC2,AC2的值分别为61,61或40,100或100,360.
28.解:过点A作AE⊥BC于点E,
∵等腰△ABC中,AB=AC=5,BC=,
∴BE=BC=,
∴AE==,
∴S△ABC=BC?AE=,
∵S△ABC=AC?BD,
∴BD==3.
29.解:连接AC,
∵△ABE≌△BCD,
∴AB=BC,AE=BD,BE=CD,∠BAE=∠CBD,
∵∠ABE+∠BAE=90°,
∴∠ABE+∠CBE=90°,
∴∠ABC=90°,
∴S四边形ABCD=S△ABD+S△BDC=BD?AE+BD?CD=AE?AE+AE?BE=BE2+BD?BE,
又∵S四边形ABCD=S△ABC+S△ADC=AB?BC+CD?DE=AB?AB+BE?DE=AB2+BE?DE,
∴BE2+AE?BE=AB2+BE?DE,
∴AB2=BE2+BD?BE﹣BE?DE,
∴AB2=BE2+(BD﹣DE)?BE,即AB2=BE2+AE2.
30.证明:连接DB,过点D作BC边上的高DF,交BC的延长线与点F,
则四边形DFCE为长方形,所以DF=EC=b﹣a.(用含字母的代数式表示)
因为S四边形ABCD=S△ACD+S△ABC=+;
S四边形ABCD=S△ADB+S△DCB=;
所以;
所以a2+b2=c2.
故答案为:b﹣a;S△ABC;;S△DCB;;;;a2+b2=c2.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
