北师大版八年级数学上册《4.4 一次函数的应用》 同步练习(word版含答案)
文档属性
| 名称 | 北师大版八年级数学上册《4.4 一次函数的应用》 同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 354.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 18:42:53 | ||
图片预览



文档简介
4.4
一次函数的应用
一.选择题
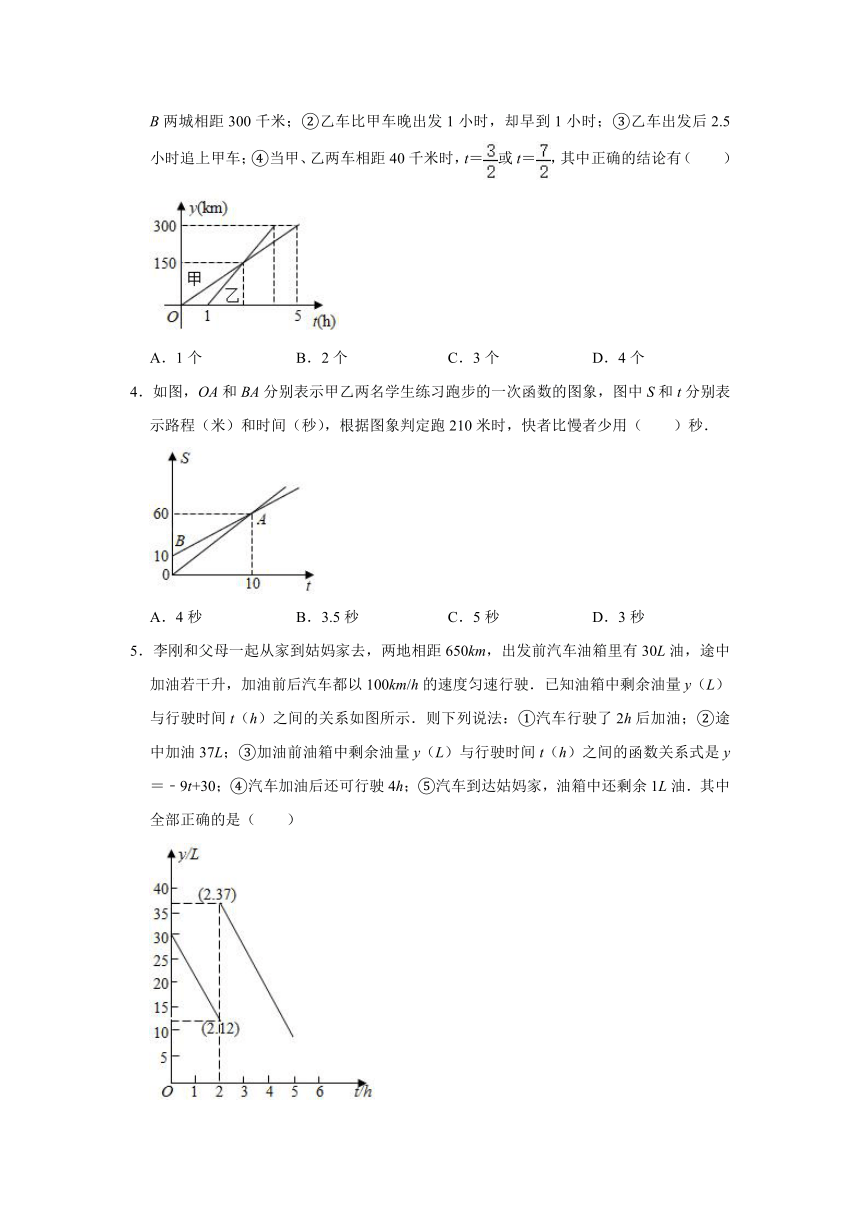
1.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=800;④a=30.以上结论正确的有( )
A.①②
B.①②③
C.①③④
D.①②④
2.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.下列四种说法:其中正确的个数是( )
①每分钟的进水量为5升.
②每分钟的出水量为3.75升.
③从计时开始8分钟时,容器内的水量为25升.
④容器从进水开始到水全部放完的时间是20分钟.
A.1个
B.2个
C.3个
D.4个
3.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=或t=,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
4.如图,OA和BA分别表示甲乙两名学生练习跑步的一次函数的图象,图中S和t分别表示路程(米)和时间(秒),根据图象判定跑210米时,快者比慢者少用( )秒.
A.4秒
B.3.5秒
C.5秒
D.3秒
5.李刚和父母一起从家到姑妈家去,两地相距650km,出发前汽车油箱里有30L油,途中加油若干升,加油前后汽车都以100km/h的速度匀速行驶.已知油箱中剩余油量y(L)与行驶时间t(h)之间的关系如图所示.则下列说法:①汽车行驶了2h后加油;②途中加油37L;③加油前油箱中剩余油量y(L)与行驶时间t(h)之间的函数关系式是y=﹣9t+30;④汽车加油后还可行驶4h;⑤汽车到达姑妈家,油箱中还剩余1L油.其中全部正确的是( )
A.①④⑤
B.①③
C.②⑤
D.③④⑤
6.一辆货车从A地开往B地,一辆小汽车从B地开往A地,同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),s与t之间的函数关系如图所示,下列说法:
①A、B两地相距60千米:
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米;
⑤出发2小时,小货车离终点还有80千米,其中正确的有( )
A.5个
B.4个
C.3个
D.2个
7.甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( )
A.甲车的平均速度为60km/h
B.乙车的平均速度为100km/h
C.乙车比甲车先到B城
D.乙车比甲车先出发1h
8.甲、乙两人进行1500米比赛,在比赛过程中,两人所跑的路程y(米)与所用的时间x(分)的函数关系如图所示,则下列说法正确的是( )
A.甲先到达终点
B.跑到两分钟时,两人相距200米
C.甲的速度随时间增大而增大
D.起跑两分钟后,甲的速度大于乙的速度
9.小甬,小真两人的跑步路程y(米)和跑步时间x(分)之间的关系如图所示,已知小甬的跑步速度比小真快,则下列说法正确的是( )
A.小甬每分钟跑200米.小真每分钟跑100米
B.小甬每跑100米时,小真只能跑60米
C.相遇时,小甬、小真两人都跑了500米
D.经过4分钟时,小甬、小真两人都跑800米
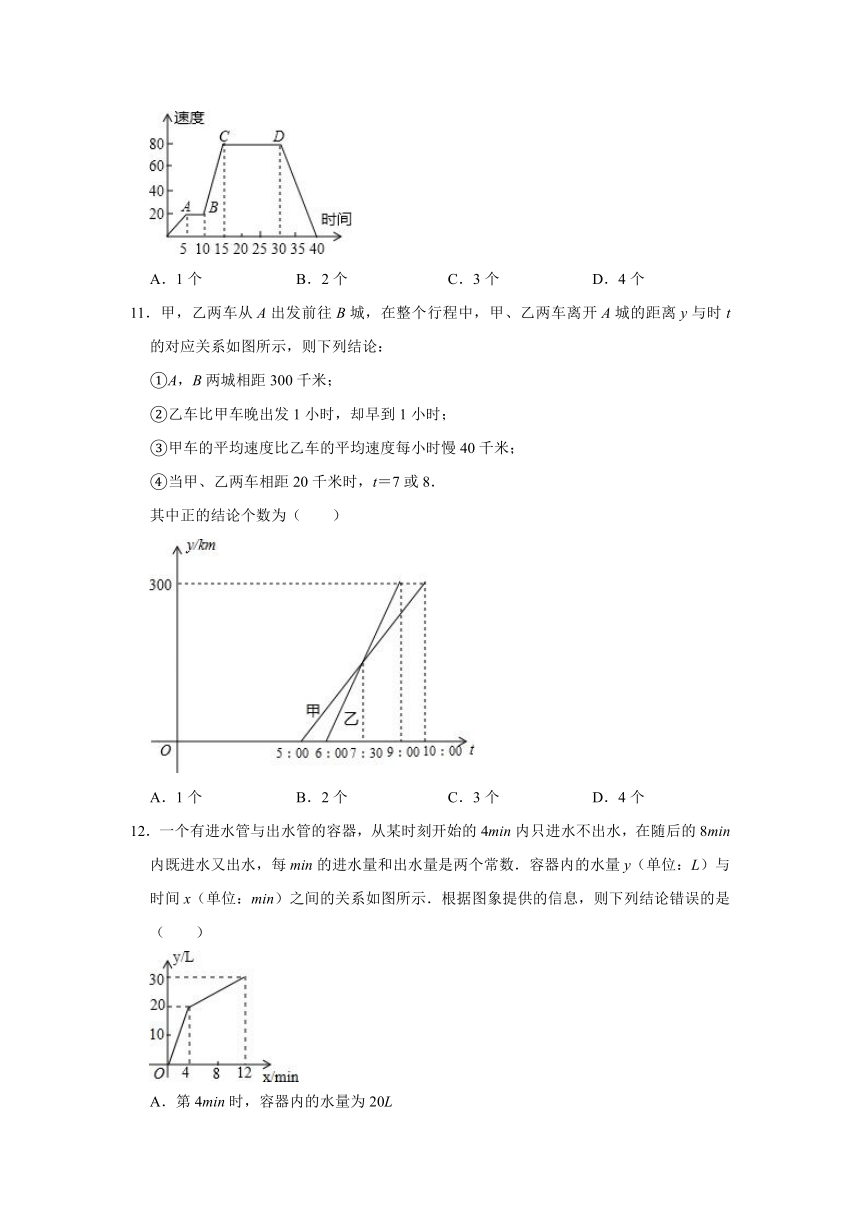
10.如图是汽车行驶速度(千米/时)?和时间(分)的关系图,下列说法其中正确的个数为( )
(1)汽车行驶时间为40分钟;
(2)AB表示汽车匀速行驶;
(3)在第30分钟时,汽车的速度是90千米/时;
(4)汽车共加速行驶了10分钟
A.1个
B.2个
C.3个
D.4个
11.甲,乙两车从A出发前往B城,在整个行程中,甲、乙两车离开A城的距离y与时t的对应关系如图所示,则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③甲车的平均速度比乙车的平均速度每小时慢40千米;
④当甲、乙两车相距20千米时,t=7或8.
其中正的结论个数为( )
A.1个
B.2个
C.3个
D.4个
12.一个有进水管与出水管的容器,从某时刻开始的4min内只进水不出水,在随后的8min内既进水又出水,每min的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.根据图象提供的信息,则下列结论错误的是( )
A.第4min时,容器内的水量为20L
B.每min进水量为5L
C.每min出水量为1.25L
D.第8min时,容器内的水量为25L
13.等腰三角形ABC中,AB=AC,记AB=x,周长为y,定义(x,y)为这个三角形的坐标.如图所示,直线y=2x,y=3x,y=4x将第一象限划分为4个区域.下面四个结论中,
①对于任意等腰三角形ABC,其坐标不可能位于区域Ⅰ中;
②对于任意等腰三角形ABC,其坐标可能位于区域Ⅳ中;
③若三角形ABC是等腰直角三角形,其坐标位于区域Ⅲ中;
④图中点M所对应等腰三角形的底边比点N所对应等腰三角形的底边长.
所有正确结论的序号是( )
A.①③
B.①③④
C.②④
D.①②③
14.如图,直线y=﹣x+6分别与x、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处.以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(,);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的坐标是(,).
正确的结论是( )
A.①②
B.①②③
C.①③④
D.①②③④
15.如图,在平面直角坐标系中,直线y=﹣x+4与x轴交于点A,与y轴交于点B,点C是AB的中点,∠ECD绕点C按顺时针旋转,且∠ECD=45°,∠ECD的一边CE交y轴于点F,开始时另一边CD经过点O,点G坐标为(﹣2,0),当∠ECD旋转过程中,射线CD与x轴的交点由点O到点G的过程中,则经过点B、C、F三点的圆的圆心所经过的路径长为( )
A.
B.
C.
D.
二.填空题
16.甲、乙两地相距360km,一辆货车从甲地以60km/h的速度匀速前往乙地,到达乙地后停止.在货车出发的同时,另一辆轿车从乙地沿同一公路匀速前往甲地,到达甲地后停止.两车之间的路程y(km)与货车出发时间x(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.其中点C的坐标是(0,360),点D的坐标是(2,0),则点E的坐标是
.
17.某快递公司快递员甲匀速骑车去距公司6000米的某小区取物件,出发几分钟后,该公司快递员乙发现甲的手机落在公司,于是立马匀速骑车去追赶甲,乙出发几分钟后,甲也发现自己的手机落在了公司,立即调头以原速的2倍原路返回,1分钟后遇到了乙,乙把手机给甲后,乙以原速的一半原路返回公司,甲以返回时的速度继续去小区取物件,刚好在事先预计的时间到达该小区.甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(给手机及中途其它耽误时间忽略不计),则甲到小区时,乙距公司的路程是
米.
18.“赛龙舟”是我国的一个传统运动项目.某天,甲乙两队在一个笔直的湖面进行“赛龙舟”比赛,全程300米.两队同时出发,刚出发,乙队就以明显优势领先,甲队发现形式不利,迅速调整比赛状态,把速度提升了,并以提升后的速度赛完全程,假设乙队全程是匀速比赛状态,甲队提速前和提速后也分别是匀速运动,甲、乙两队之间的距离y(米)与乙队行驶x(秒)之间的关系如图所示,则甲队到达终点时,乙队离终点还有
米.
19.如图所示,王芳,李莉两人分别从A、B两地出发,相向而行,已知李莉先出发4分钟后,王芳才出发,他们两人相遇后,李莉立即以原速返回B地,王芳以原速继续向B地前行,王芳、李莉分别到达B地后都停止行走,王芳、李莉两人相距的路程y(米)与李莉出发的时间x(分钟)之间的关系如图所示,则王芳到达B地时,李莉与B地相距的路程是
米.
20.已知天目山的主峰海拔约1500m,据研究得知地面上空h(m)处的气温t与地面气温s有如下关系t=﹣kh+s,现用气象气球测得某时刻离地面200m处的气温t为8.4℃,离地面600m处的气温t为6℃,则此时天目山主峰的气温约为
.
21.某学校创客小组进行机器人跑步大赛,机器人小A和小B从同一地点同时出发,小A在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有
(填序号).
①两个机器人第一次相遇时间是在第2分钟;
②小B每分钟跑50米;
③赛程总长200米;
④小A到达终点的时候小B距离终点还有20米.
22.小夏、小熙两同学从距学校3000米的同一小区同时出发,各自将作业本拿回学校,他们俩将作业本拿回学校后,又各自以原速原路返回自己居住的小区,在整个过程中,她们两人均保持各自的速度匀速行驶,且小夏的速度比小熙的速度快.整个过程中两人相距的路程y(米)与小夏离开小区的时间x(分钟)之间的关系如图所示(返校逗留时间不计),则小夏返回到小区时,小熙距小区的路程为
米.
23.白鹤公园风景秀丽,成为广大市民休闲锻炼的圣地,星期天,小明和爸爸到白鹤公园登山锻炼,他们同时从山脚出发,以各自的速度匀速登山,前20分钟小明以v1的速度一直在前,由于小明体力不支,休息了20分钟,这时他发现爸已超过他走在了前面,小明立即以v2的速度追赶爸爸,直到与爸爸相遇,如图是两人之间相距的路程y(米)与爸爸登山时间x(分)之间的函数图象,则=
.
24.如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,AC所在直线的函数表达式是y=2x+4,若保持AC的长不变,当点A在y轴的正半轴滑动,点C随之在x轴的负半轴上滑动,则在滑动过程中,点B与原点O的最大距离是
.
25.如图,直线y=﹣x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标
;
(2)若△OQC是等腰直角三角形,则t的值为
;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数关系式
.
三.解答题
26.下表给出了距离地面高度与所在位置的温度之间的大致关系.根据下表,请回答以下几个问题:
距离地面高度(千米)
0
1
2
3
4
5
所在位置的温度(℃)
20
14
8
2
﹣4
(1)上表反映的两个变量中,
是自变量,
是因变量;
(2)若用h表示距离地面的高度,用y表示温度,则y与h之间的关系式是:
;
当距离地面高度5千米时,所在位置的温度为:
℃.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用时间关系图.根据图象回答以下问题:
(3)返回途中飞机在2千米高空大约盘旋了
分钟.
(4)飞机发生事故16分钟后所在高空的温度是
.
27.小蕾家与外婆家相距270km,她假期去看望外婆,返回时,恰好有一辆顺路车可以带小蕾到A服务区,于是,小蕾与爸爸约定,她先搭乘顺路车到A服务区,爸爸驾车到A服务区接小蕾回家.两人在A服务区见面后,休息了一会儿,然后小蕾乘坐爸爸的车以60km/h的速度返回家中.返回途中,小蕾与自己家的距离y(km)和时间x(h)之间的关系大致如图所示.
(1)求小蕾从外婆家到A服务区的过程中,y与x之间的函数关系式;
(2)小蕾从外婆家回到自己家共用了多长时间?
28.一辆汽车的油箱中现有汽油50升,如果不再加油,那么油箱中的余油量y(单位:升)随行驶里程x(单位:千米)的增加而减少,平均每千米的耗油量为0.1升.
(1)写出y与x之间的函数关系式;
(2)汽车最多可行驶多少千米?
(3)汽车行驶200千米时,油箱中还有多少油?
(4)写出自变量x的取值范围.
29.已知,如图,点A坐标为(6,0),直线y=﹣x﹣2交y轴于点B.
(1)求直线AB的函数解析式;
(2)若点C为直线y=﹣x﹣2上第四象限内一点,且满足△ABC的面积为13,求点C的坐标;
(3)在(2)中C点坐标的条件下,在x轴上取两点M、N,点M在点N的左侧,使得MN=2,求使得四边形BMNC周长最小时点M、N的坐标.
30.如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(4,2).E为AB的中点,过点D(6,0)和点E的直线分别与BC、y轴交于点F、G.
(1)求直线DE的函数关系式;
(2)函数y=mx﹣1的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
参考答案
一.选择题
1.解:①当x=0时,y=1200,
∴A、B之间的距离为1200m,结论①正确;
②乙的速度为1200÷(24﹣4)=60(m/min),
甲的速度为1200÷12﹣60=40(m/min),
60÷40=1.5,
∴乙行走的速度是甲的1.5倍,结论②正确;
③b=(60+40)×(24﹣4﹣12)=800,结论③正确;
④a=1200÷40+4=34,结论④错误.
故结论正确的有①②③,
故选:B.
2.解:由图象可得,
每分钟的进水量为20÷4=5(L),故①正确;
每分钟的出水量为5﹣(30﹣20)÷(12﹣4)=3.75(L),故②正确;
从计时开始8分钟时,容器内的水量为:20+(8﹣4)×(5﹣3.75)=25(L),故③正确;
容器从进水开始到水全部放完的时间是:12+30÷3.75=20(分钟),故④正确;
故选:D.
3.解:由图象可知A、B两城市之间的距离为300km,故①正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
把y=150代入y甲=60t,可得:t=2.5,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(2.5,150)代入可得,
解得,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
乙的速度:150÷(2.5﹣1)=100,
乙的时间:300÷100=3,
甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故②正确;
甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③错误;
令|y甲﹣y乙|=40,可得|60t﹣100t+100|=40,即|100﹣40t|=40,
当100﹣40t=40时,可解得t=,
当100﹣40t=﹣40时,可解得t=,
又当t=时,y甲=40,此时乙还没出发,
当t=时,乙到达B城,y甲=260;
综上可知当t的值为或或或t=时,两车相距40千米,故④不正确;
故选:B.
4.解:由图象可得,
甲的速度为:60÷10=6(米/秒),
乙的速度为:(60﹣10)÷10=5(米/秒),
(210﹣10)÷5﹣210÷6
=40﹣35
=5(秒),
故选:C.
5.解:由图象可得,
汽车行驶了2h后加油,故①正确;
途中加油37﹣12=25(L),故②错误;
设加油前油箱中剩余油量y(L)与行驶时间t(h)之间的函数关系式是y=kt+b,
,解得,
即加油前油箱中剩余油量y(L)与行驶时间t(h)之间的函数关系式是y=﹣9t+30,故③正确;
汽车加油后还可行驶37÷[(30﹣12)÷2]=4(小时),故④错误;
650÷100=6.5(小时),
2+4<6.5,
故汽车加油后不能到达姑妈家,故⑤错误;
故选:B.
6.解:由图象可得,
A、B两地相距120千米,故①错误;
出发1小时,货车与小汽车相遇,故②正确;
小汽车的速度是120÷1.5=80(千米/小时),货车的速度为:120÷3=40(千米/小时),即小汽车的速度是货车速度的80÷40=2倍,故③正确;
出发1.5小时,小汽车比货车多行驶了(80﹣40)×1.5=60(千米),故④正确;
出发2小时,小货车离终点还有120﹣40×2=40(千米),故⑤错误;
故选:C.
7.解:由图象知:
A.甲车的平均速度为=60km/h,故A选项不合题意;
B.乙车的平均速度为=100km/h,故B选项不合题意;
C.甲10时到达B城,乙9时到达B城,所以乙比甲先到B城,故C选项不合题意;
D.甲5时出发,乙6时出发,所以乙比甲晚出发1h,故此选项错误,
故选:D.
8.解:由图象可得,
乙先到达终点,故选项A错误;
甲的速度为:1500÷5=300(米/分),故当跑到两分钟时,两人相距300×2﹣400=200(米),故选项B正确;
甲的速度保持不变,故选项C错误;
起跑两分钟后,乙的速度大于甲的速度,故选项D错误;
故选:B.
9.解:∵小甬的跑步速度比小真快,
∴小甬的图象经过原点,
设小真跑步路程y(米)和跑步时间x(分)之间的关系式为y=kx+200,则800=4k+200,解得k=150,
∴小真跑步路程y(米)和跑步时间x(分)之间的关系式为y=150x+200,
150×2+200=500,
∴小甬的图象经过(2,500),
∴小甬路程y(米)和跑步时间x(分)之间的关系式为y=250x,
∴小甬的速度:小真的速度=250:150,
∴小甬每跑100米时,小真只能跑60米.
故选:B.
10.解:读图可得,在x=40时,速度为0,故(1)正确;
AB段,y的值相等,故速度不变,故(2)正确;
x=30时,y=80,即在第30分钟时,汽车的速度是80千米/时;故(3)错误;
汽车共加速行驶的时间为:5+(15﹣10)=10(分钟),故(4)正确.
综上可得(1)(2)(4)正确,共3个.
故选:C.
11.解:①由题可得,A,B两城相距300千米,故①正确;
②由图可得,乙车比甲车晚出发1小时,却早到1小时,故②正确;
③甲车的平均速度为300÷(10﹣5)=60(km/h),乙车的平均速度为300÷(9﹣6)=100(km/h),所以甲车的平均速度比乙车的平均速度每小时慢40千米故③正确;
④相遇前:60(t﹣5)﹣100(t﹣6)=20,解得t=7;
相遇后:100(t﹣6)﹣60(t﹣5)=20,解得t=8.
当乙到底B城后,5+(300﹣20)÷60=;
即当甲、乙两车相距20千米时,t=7或8或.
故④错误.
即正的结论个数为3个.
故选:C.
12.解:由图象可得,
第4min时,容器内的水量为20L,故选项A正确;
每min进水量为:20÷4=5(L),故选项B正确;
每min出水量为:5﹣(30﹣20)÷(12﹣4)=3.75(L),故选项C错误;
第8min时,容器内的水量为:20+(8﹣4)×(5﹣3.75)=25(L),故选项D正确;
故选:C.
13.解:如图,等腰三角形ABC中,AB=AC,记AB=x,周长为y,
设BC=z,则y=2x+z,x>0,z>0.
①∵BC=z>0,
∴y=2x+z>2x,
∴对于任意等腰三角形ABC,其坐标位于直线y=2x的上方,不可能位于区域Ⅰ中,故结论①正确;
②∵三角形任意两边之和大于第三边,
∴2x>z,即z<2x,
∴y=2x+z<4x,
∴对于任意等腰三角形ABC,其坐标位于直线y=4x的下方,不可能位于区域Ⅳ中,故结论②错误;
③若三角形ABC是等腰直角三角形,则z=x,
∵1<<2,AB=x>0,
∴x<x<2x,
∴3x<2x+x<4x,
即3x<y<4x,
∴若三角形ABC是等腰直角三角形,其坐标位于区域Ⅲ中,故结论③正确;
④由图可知,点M位于区域Ⅲ中,此时3x<y<4x,
∴3x<2x+z<4x,
∴x<z<2x;
点N位于区域Ⅱ中,此时2x<y<3x,
∴2x<2x+z<3x,
∴0<z<x;
∴图中点M所对应等腰三角形的底边比点N所对应等腰三角形的底边长,故结论④正确.
故选:B.
14.解:∵直线y=﹣x+6分别与x、y轴交于点A、B,
∴点A(8,0),点B(0,6),
∴OA=8,OB=6,
∴AB===10,故①正确;
∵线段OB沿BC翻折,点O落在AB边上的点D处,
∴OB=BD=6,OC=CD,∠BOC=∠BDC=90°,
∴AD=AB﹣BD=4,
∵AC2=AD2+CD2,
∴(8﹣OC)2=16+OC2,
∴OC=3,
∴点C(3,0),
设直线BC解析式为:y=kx+6,
∴0=3k+6,
∴k=﹣2,
∴直线BC解析式为:y=﹣2x+6,故②正确;
如图,过点D作DH⊥AC于H,
∵CD=OC=3,
∴CA=5,
∵S△ACD=AC×DH=CD×AD,
∴DH==,
∴当y=时,=﹣x+6,
∴x=,
∴点D(,),故③正确;
∵线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,且OC=CD,
∴PD∥OC,
∴点P纵坐标为,故④错误,
故选:B.
15.解:∵直线y=﹣x+4与x轴交于点A,与y轴交于点B,
∴B(0,4),A(4,0),
∵点C是AB的中点,
∴C(2,2),
①当一边CD经过点O时,点F的坐标为(0,2),此时点F、B、C三点的圆心为BC的中点,坐标为(1,3);
②当直线CD过点G时,如图
取OB的中点N,连接CN,OC,则CN=ON=2,
∴OC=2,
∵G(﹣2,0),
∴直线GC的解析式为:y=x+1,
∴直线GC与y轴交点M(0,1),
过点M作MH⊥OC,
∵∠MOH=45,
∴MH=OH=,
∴CH=OC﹣OH=,
∵∠NCO=∠FCG=45°,
∴∠FCN=∠MCH,
又∵∠FNC=∠MHC,
∴△FNC∽△MHC,
∴,即,
得FN=,
∴OF=2+=.
∴F(,0),
此时过点F、B、C三点的圆心在BF的垂直平分线上,设圆心坐标为(x,),
则,
解得x=,
当∠ECD旋转过程中,射线CD与x轴的交点由点O到点G的过程中,则经过点B、C、F三点的圆的圆心所经过的路径为线段,
即由BC的中点到点(,),
∴所经过的路径长==.
故选:A.
二.填空题
16.解:由题意可得,
轿车的速度为:360÷2﹣60=120(km/h),
则点E的横坐标为:360÷120=3,纵坐标为:60×(3﹣2)+120×(3﹣2)=180,
故点E的坐标为(3,180),
故答案为:(3,180).
17.解:设甲开始的速度为a(m/min),则甲后来的速度为2a(m/min),
由题意可得,9+,
解得,a=500,
设乙的速度为b(m/min),由甲乙相遇知,
(9﹣)b+2a?1=(9﹣1)a,
∴b=1000,
∴甲乙相遇时乙距公司的路程为:(9﹣)×1000=3000,
甲到达小区的时间为:=12(min),
∴甲到小区时,乙距公司的路程为:3000﹣1000××(12﹣9)=1500(m),
故答案为:1500.
18.解:由图可得,
乙队的速度为300÷100=3(米/秒),
设甲队开始的速度为a米/秒,
15(3﹣a)=(45﹣15)×[a(1+)﹣3],
解得a=2,
∴甲队提速后的速度为2×(1+)=3.5(米/秒),
∴甲队到达终点用的时间为:15+(300﹣15×2)÷3.5=15+=15+77=92(秒),
∴甲队到达终点时,乙队离终点还有3×(100﹣92)=3×7=3×=(米),
故答案为:.
19.解:由题意可得,
李莉的速度为:(1500﹣1300)÷4=50(米/分),
王芳的速度为:(1300﹣390)÷(11﹣4)﹣50=80(米/分),
王芳、李莉相遇时的时间为:1300÷(50+80)+4=14(分钟),
∴李莉距离B地的路程为:50×14=700(米),
∵王芳到达B地时间的时间为:1300÷80+2=(分),
∴王芳到达B地时,李莉与B地相距的路程是:700×2﹣50×﹣200=287.5(米),
故答案为:287.5.
20.解:∵t=﹣kh+s,某时刻离地面200m处的气温t为8.4℃,离地面600m处的气温t为6℃,
∴,
解得,
∴t=﹣0.006h+9.6,
当h=1500时,t=﹣0.006×1500+9.6=0.6,
即此时天目山主峰的气温约为0.6℃,
故答案为:0.6℃.
21.解:根据题意结合图象可知小A在第1到第3分钟的速度为:(米/分),
∴两个机器人第一次相遇时间是在:1+=2(分钟),故①正确;
小B的速度为:80÷2=40(米/分),故②错误;
小A第3分钟后的速度为:(米/分),
∴赛程总长:100+80=180(米),故③错误;
180﹣40×4=20(米),
即小A到达终点的时候小B距离终点还有20米,故④正确.
综上所述,正确的有①④.
故答案为:①④
22.解:的速度为:3000÷20=150(米/分),
小熙的速度为:3000÷30=100(米/分),
小夏返回到小区的时间为:3000×2÷150=40(分),
在小夏返回到小区时,小熙走的总路程为:100×40=4000(米),
∴小夏返回到小区时,小熙距小区的路程为:3000×2﹣4000=2000(米).
故答案为:2000.
23.解:爸爸的速度为:1000×2÷20=100(米/分钟),
v1=1000÷20+100=150(米/分钟),
v2=1000÷10+100=200(米/分钟),
∴=.
故答案为:.
24.解:当x=0时,y=2x+4=4,
∴A(0,4);
当y=2x+4=0时,x=﹣2,
∴C(﹣2,0).
∴OA=4,OC=2,
∴AC==2.
如图所示,过点B作BD⊥x轴于点D.
∵∠ACO+∠ACB+∠BCD=180°,∠ACO+∠CAO=90°,∠ACB=90°,
∴∠CAO=∠BCD.
在△AOC和△CDB中,,
∴△AOC≌△CDB(AAS),
∴CD=AO=4,DB=OC=2,
OD=OC+CD=6,
∴点B的坐标为(﹣6,2).
如图所示.取AC的中点E,连接BE,OE,OB,
∵∠AOC=90°,AC=2,
∴OE=CE=AC=,
∵BC⊥AC,BC=2,
∴BE==5,
若点O,E,B不在一条直线上,则OB<OE+BE=5+.
若点O,E,B在一条直线上,则OB=OE+BE=5+,
∴当O,E,B三点在一条直线上时,OB取得最大值,最大值为5+,
故答案为:5+.
25.解:(1)∵由,得,
∴C(2,2);
(2)如图1,当∠CQO=90°,CQ=OQ,
∵C(2,2),
∴OQ=CQ=2,
∴t=2,
②如图2,当∠OCQ=90°,OC=CQ,
过C作CM⊥OA于M,
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴t=2+2=4,
即t的值为2或4,
故答案为:2或4;
(3)令﹣x+3=0,得x=6,由题意:Q(3,0),
设直线CQ的解析式是y=kx+b,
把C(2,2),Q(3,0)代入得:,
解得:k=﹣2,b=6,
∴直线CQ对应的函数关系式为:y=﹣2x+6.
故答案为:(1)(2,2);(3)y=﹣2x+6.
三.解答题
26.解:(1)根据函数的定义:距离地面高度是自变量,所在位置的温度是因变量,
故答案为:距离地面高度,所在位置的温度;
(2)由题意得:y=20﹣6h,
当x=5时,y=﹣10,
故答案为:y=20﹣6h,﹣10;
(3)从图象上看,h=2时,持续的时间为2分钟,
即返回途中飞机在2千米高空水平大约盘旋了2分钟;
故答案为:2;
(4)当h=2时,y=20﹣12=8,
即飞机发生事故时所在高空的温度是8度,
故答案为:8度.
27.解:(1)设y与x之间的函数关系式为y=kx+b,根据题意得:
,
解得,
∴y与x之间的函数关系式为y=﹣90x+270(0≤x≤2);
(2)把x=2代入y=﹣90x+270,得y=﹣180+270=90,
从A服务区到家的时间为:90÷60=1.5(小时),
2.5+1.5=4(小时),
答:小蕾从外婆家回到自己家共用了4小时.
28.解:(1)根据题意,每行程x千米,耗油0.1x升,即总油量减少0.1x升,
则油箱中的油剩下(50﹣0.1x)升,
∴y与x的函数关系式为:y=50﹣0.1x;
(2)当y=0时,50﹣0.1x=0,
解得x=500,
所以汽车最多可行驶500千米;
(3)当x=200时,代入x,y的关系式:
y=50﹣0.1×200=30.
所以,汽车行驶200km时,油桶中还有30升汽油;
(4)因为x代表的实际意义为行驶里程,所以x不能为负数,即x≥0;
又行驶中的耗油量为0.1x,不能超过油箱中现有汽油量的值50,
即0.1x≤50,
解得,x≤500.
综上所述,自变量x的取值范围是0≤x≤500.
29.解:(1)对于y=﹣x﹣2,令x=0,则y=﹣2,故点B(0,﹣2),
设直线AB的表达式为y=kx+b,则,解得,
故直线AB的表达式为y=x﹣2;
(2)连接OC,
则△ABC的面积=S四边形OBCA﹣S△AOB=×OB×xC+AO×|yC|﹣×AO×OB=13,
即×2×xC+×6×(﹣yC)﹣×2×6=13,
即﹣3yC+xC=19①,
而yC=﹣xC﹣2②,
联立①②并解得,即点C(4,﹣5);
(3)作点C关于x轴的对称点C′(4,5),将点C′向左平移2个单位得到点C″(2,5),
连接BC″交x轴于点M,将点M向右平移2个单位得到点N,则点M、N为所求点,此时四边形BMNC周长最小,
理由:∵MN∥C″C′且MN=C″C′,故四边形MNC′C″为平行四边形,
故C′N=C″M=CN,
则四边形BMNC周长=MN+BM+BC+CN=MN+BM+BC+C′N=MN+BM+BC+C″M=CB+MN+BC″为最小,
由点B、C″的坐标得,直线BC″的表达式为y=x﹣2,
令y=0,即y=x﹣2=0,解得x=,
故点M、N的坐标分别为(,0)、(,0).
30.解:(1)设直线DE的解析式为:y=kx+b,
∵顶点B的坐标为(4,2),E为AB的中点,
∴点E的坐标为:(4,1),
∵D(6,0),
则,解得,
∴直线DE的函数关系式为:y=﹣x+3;
(2)∵点F的纵坐标为2,且点F在直线DE上,
∴﹣x+3=2,
解得:x=2,
∴点F的坐标为(2,2);
∵函数y=mx﹣1的图象经过点F,
∴2m﹣1=2,
解得:m=;
(3)如图:设直线FH交y轴于点K,
对于y=x﹣1,
当y=0时,x﹣1=0,解得x=,即H(,0),
令x=0,则y=﹣1,则点K(0,﹣1);
同理可得,点G(0,3),则KG=4,
四边形OHFG的面积=S△GKF﹣S△OHK=×4×2﹣×1×=.
一次函数的应用
一.选择题
1.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=800;④a=30.以上结论正确的有( )
A.①②
B.①②③
C.①③④
D.①②④
2.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系如图所示.下列四种说法:其中正确的个数是( )
①每分钟的进水量为5升.
②每分钟的出水量为3.75升.
③从计时开始8分钟时,容器内的水量为25升.
④容器从进水开始到水全部放完的时间是20分钟.
A.1个
B.2个
C.3个
D.4个
3.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=或t=,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
4.如图,OA和BA分别表示甲乙两名学生练习跑步的一次函数的图象,图中S和t分别表示路程(米)和时间(秒),根据图象判定跑210米时,快者比慢者少用( )秒.
A.4秒
B.3.5秒
C.5秒
D.3秒
5.李刚和父母一起从家到姑妈家去,两地相距650km,出发前汽车油箱里有30L油,途中加油若干升,加油前后汽车都以100km/h的速度匀速行驶.已知油箱中剩余油量y(L)与行驶时间t(h)之间的关系如图所示.则下列说法:①汽车行驶了2h后加油;②途中加油37L;③加油前油箱中剩余油量y(L)与行驶时间t(h)之间的函数关系式是y=﹣9t+30;④汽车加油后还可行驶4h;⑤汽车到达姑妈家,油箱中还剩余1L油.其中全部正确的是( )
A.①④⑤
B.①③
C.②⑤
D.③④⑤
6.一辆货车从A地开往B地,一辆小汽车从B地开往A地,同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),s与t之间的函数关系如图所示,下列说法:
①A、B两地相距60千米:
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米;
⑤出发2小时,小货车离终点还有80千米,其中正确的有( )
A.5个
B.4个
C.3个
D.2个
7.甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( )
A.甲车的平均速度为60km/h
B.乙车的平均速度为100km/h
C.乙车比甲车先到B城
D.乙车比甲车先出发1h
8.甲、乙两人进行1500米比赛,在比赛过程中,两人所跑的路程y(米)与所用的时间x(分)的函数关系如图所示,则下列说法正确的是( )
A.甲先到达终点
B.跑到两分钟时,两人相距200米
C.甲的速度随时间增大而增大
D.起跑两分钟后,甲的速度大于乙的速度
9.小甬,小真两人的跑步路程y(米)和跑步时间x(分)之间的关系如图所示,已知小甬的跑步速度比小真快,则下列说法正确的是( )
A.小甬每分钟跑200米.小真每分钟跑100米
B.小甬每跑100米时,小真只能跑60米
C.相遇时,小甬、小真两人都跑了500米
D.经过4分钟时,小甬、小真两人都跑800米
10.如图是汽车行驶速度(千米/时)?和时间(分)的关系图,下列说法其中正确的个数为( )
(1)汽车行驶时间为40分钟;
(2)AB表示汽车匀速行驶;
(3)在第30分钟时,汽车的速度是90千米/时;
(4)汽车共加速行驶了10分钟
A.1个
B.2个
C.3个
D.4个
11.甲,乙两车从A出发前往B城,在整个行程中,甲、乙两车离开A城的距离y与时t的对应关系如图所示,则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③甲车的平均速度比乙车的平均速度每小时慢40千米;
④当甲、乙两车相距20千米时,t=7或8.
其中正的结论个数为( )
A.1个
B.2个
C.3个
D.4个
12.一个有进水管与出水管的容器,从某时刻开始的4min内只进水不出水,在随后的8min内既进水又出水,每min的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.根据图象提供的信息,则下列结论错误的是( )
A.第4min时,容器内的水量为20L
B.每min进水量为5L
C.每min出水量为1.25L
D.第8min时,容器内的水量为25L
13.等腰三角形ABC中,AB=AC,记AB=x,周长为y,定义(x,y)为这个三角形的坐标.如图所示,直线y=2x,y=3x,y=4x将第一象限划分为4个区域.下面四个结论中,
①对于任意等腰三角形ABC,其坐标不可能位于区域Ⅰ中;
②对于任意等腰三角形ABC,其坐标可能位于区域Ⅳ中;
③若三角形ABC是等腰直角三角形,其坐标位于区域Ⅲ中;
④图中点M所对应等腰三角形的底边比点N所对应等腰三角形的底边长.
所有正确结论的序号是( )
A.①③
B.①③④
C.②④
D.①②③
14.如图,直线y=﹣x+6分别与x、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处.以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(,);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的坐标是(,).
正确的结论是( )
A.①②
B.①②③
C.①③④
D.①②③④
15.如图,在平面直角坐标系中,直线y=﹣x+4与x轴交于点A,与y轴交于点B,点C是AB的中点,∠ECD绕点C按顺时针旋转,且∠ECD=45°,∠ECD的一边CE交y轴于点F,开始时另一边CD经过点O,点G坐标为(﹣2,0),当∠ECD旋转过程中,射线CD与x轴的交点由点O到点G的过程中,则经过点B、C、F三点的圆的圆心所经过的路径长为( )
A.
B.
C.
D.
二.填空题
16.甲、乙两地相距360km,一辆货车从甲地以60km/h的速度匀速前往乙地,到达乙地后停止.在货车出发的同时,另一辆轿车从乙地沿同一公路匀速前往甲地,到达甲地后停止.两车之间的路程y(km)与货车出发时间x(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.其中点C的坐标是(0,360),点D的坐标是(2,0),则点E的坐标是
.
17.某快递公司快递员甲匀速骑车去距公司6000米的某小区取物件,出发几分钟后,该公司快递员乙发现甲的手机落在公司,于是立马匀速骑车去追赶甲,乙出发几分钟后,甲也发现自己的手机落在了公司,立即调头以原速的2倍原路返回,1分钟后遇到了乙,乙把手机给甲后,乙以原速的一半原路返回公司,甲以返回时的速度继续去小区取物件,刚好在事先预计的时间到达该小区.甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(给手机及中途其它耽误时间忽略不计),则甲到小区时,乙距公司的路程是
米.
18.“赛龙舟”是我国的一个传统运动项目.某天,甲乙两队在一个笔直的湖面进行“赛龙舟”比赛,全程300米.两队同时出发,刚出发,乙队就以明显优势领先,甲队发现形式不利,迅速调整比赛状态,把速度提升了,并以提升后的速度赛完全程,假设乙队全程是匀速比赛状态,甲队提速前和提速后也分别是匀速运动,甲、乙两队之间的距离y(米)与乙队行驶x(秒)之间的关系如图所示,则甲队到达终点时,乙队离终点还有
米.
19.如图所示,王芳,李莉两人分别从A、B两地出发,相向而行,已知李莉先出发4分钟后,王芳才出发,他们两人相遇后,李莉立即以原速返回B地,王芳以原速继续向B地前行,王芳、李莉分别到达B地后都停止行走,王芳、李莉两人相距的路程y(米)与李莉出发的时间x(分钟)之间的关系如图所示,则王芳到达B地时,李莉与B地相距的路程是
米.
20.已知天目山的主峰海拔约1500m,据研究得知地面上空h(m)处的气温t与地面气温s有如下关系t=﹣kh+s,现用气象气球测得某时刻离地面200m处的气温t为8.4℃,离地面600m处的气温t为6℃,则此时天目山主峰的气温约为
.
21.某学校创客小组进行机器人跑步大赛,机器人小A和小B从同一地点同时出发,小A在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有
(填序号).
①两个机器人第一次相遇时间是在第2分钟;
②小B每分钟跑50米;
③赛程总长200米;
④小A到达终点的时候小B距离终点还有20米.
22.小夏、小熙两同学从距学校3000米的同一小区同时出发,各自将作业本拿回学校,他们俩将作业本拿回学校后,又各自以原速原路返回自己居住的小区,在整个过程中,她们两人均保持各自的速度匀速行驶,且小夏的速度比小熙的速度快.整个过程中两人相距的路程y(米)与小夏离开小区的时间x(分钟)之间的关系如图所示(返校逗留时间不计),则小夏返回到小区时,小熙距小区的路程为
米.
23.白鹤公园风景秀丽,成为广大市民休闲锻炼的圣地,星期天,小明和爸爸到白鹤公园登山锻炼,他们同时从山脚出发,以各自的速度匀速登山,前20分钟小明以v1的速度一直在前,由于小明体力不支,休息了20分钟,这时他发现爸已超过他走在了前面,小明立即以v2的速度追赶爸爸,直到与爸爸相遇,如图是两人之间相距的路程y(米)与爸爸登山时间x(分)之间的函数图象,则=
.
24.如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,AC所在直线的函数表达式是y=2x+4,若保持AC的长不变,当点A在y轴的正半轴滑动,点C随之在x轴的负半轴上滑动,则在滑动过程中,点B与原点O的最大距离是
.
25.如图,直线y=﹣x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标
;
(2)若△OQC是等腰直角三角形,则t的值为
;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数关系式
.
三.解答题
26.下表给出了距离地面高度与所在位置的温度之间的大致关系.根据下表,请回答以下几个问题:
距离地面高度(千米)
0
1
2
3
4
5
所在位置的温度(℃)
20
14
8
2
﹣4
(1)上表反映的两个变量中,
是自变量,
是因变量;
(2)若用h表示距离地面的高度,用y表示温度,则y与h之间的关系式是:
;
当距离地面高度5千米时,所在位置的温度为:
℃.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用时间关系图.根据图象回答以下问题:
(3)返回途中飞机在2千米高空大约盘旋了
分钟.
(4)飞机发生事故16分钟后所在高空的温度是
.
27.小蕾家与外婆家相距270km,她假期去看望外婆,返回时,恰好有一辆顺路车可以带小蕾到A服务区,于是,小蕾与爸爸约定,她先搭乘顺路车到A服务区,爸爸驾车到A服务区接小蕾回家.两人在A服务区见面后,休息了一会儿,然后小蕾乘坐爸爸的车以60km/h的速度返回家中.返回途中,小蕾与自己家的距离y(km)和时间x(h)之间的关系大致如图所示.
(1)求小蕾从外婆家到A服务区的过程中,y与x之间的函数关系式;
(2)小蕾从外婆家回到自己家共用了多长时间?
28.一辆汽车的油箱中现有汽油50升,如果不再加油,那么油箱中的余油量y(单位:升)随行驶里程x(单位:千米)的增加而减少,平均每千米的耗油量为0.1升.
(1)写出y与x之间的函数关系式;
(2)汽车最多可行驶多少千米?
(3)汽车行驶200千米时,油箱中还有多少油?
(4)写出自变量x的取值范围.
29.已知,如图,点A坐标为(6,0),直线y=﹣x﹣2交y轴于点B.
(1)求直线AB的函数解析式;
(2)若点C为直线y=﹣x﹣2上第四象限内一点,且满足△ABC的面积为13,求点C的坐标;
(3)在(2)中C点坐标的条件下,在x轴上取两点M、N,点M在点N的左侧,使得MN=2,求使得四边形BMNC周长最小时点M、N的坐标.
30.如图,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(4,2).E为AB的中点,过点D(6,0)和点E的直线分别与BC、y轴交于点F、G.
(1)求直线DE的函数关系式;
(2)函数y=mx﹣1的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
参考答案
一.选择题
1.解:①当x=0时,y=1200,
∴A、B之间的距离为1200m,结论①正确;
②乙的速度为1200÷(24﹣4)=60(m/min),
甲的速度为1200÷12﹣60=40(m/min),
60÷40=1.5,
∴乙行走的速度是甲的1.5倍,结论②正确;
③b=(60+40)×(24﹣4﹣12)=800,结论③正确;
④a=1200÷40+4=34,结论④错误.
故结论正确的有①②③,
故选:B.
2.解:由图象可得,
每分钟的进水量为20÷4=5(L),故①正确;
每分钟的出水量为5﹣(30﹣20)÷(12﹣4)=3.75(L),故②正确;
从计时开始8分钟时,容器内的水量为:20+(8﹣4)×(5﹣3.75)=25(L),故③正确;
容器从进水开始到水全部放完的时间是:12+30÷3.75=20(分钟),故④正确;
故选:D.
3.解:由图象可知A、B两城市之间的距离为300km,故①正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
把y=150代入y甲=60t,可得:t=2.5,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(2.5,150)代入可得,
解得,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
乙的速度:150÷(2.5﹣1)=100,
乙的时间:300÷100=3,
甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故②正确;
甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③错误;
令|y甲﹣y乙|=40,可得|60t﹣100t+100|=40,即|100﹣40t|=40,
当100﹣40t=40时,可解得t=,
当100﹣40t=﹣40时,可解得t=,
又当t=时,y甲=40,此时乙还没出发,
当t=时,乙到达B城,y甲=260;
综上可知当t的值为或或或t=时,两车相距40千米,故④不正确;
故选:B.
4.解:由图象可得,
甲的速度为:60÷10=6(米/秒),
乙的速度为:(60﹣10)÷10=5(米/秒),
(210﹣10)÷5﹣210÷6
=40﹣35
=5(秒),
故选:C.
5.解:由图象可得,
汽车行驶了2h后加油,故①正确;
途中加油37﹣12=25(L),故②错误;
设加油前油箱中剩余油量y(L)与行驶时间t(h)之间的函数关系式是y=kt+b,
,解得,
即加油前油箱中剩余油量y(L)与行驶时间t(h)之间的函数关系式是y=﹣9t+30,故③正确;
汽车加油后还可行驶37÷[(30﹣12)÷2]=4(小时),故④错误;
650÷100=6.5(小时),
2+4<6.5,
故汽车加油后不能到达姑妈家,故⑤错误;
故选:B.
6.解:由图象可得,
A、B两地相距120千米,故①错误;
出发1小时,货车与小汽车相遇,故②正确;
小汽车的速度是120÷1.5=80(千米/小时),货车的速度为:120÷3=40(千米/小时),即小汽车的速度是货车速度的80÷40=2倍,故③正确;
出发1.5小时,小汽车比货车多行驶了(80﹣40)×1.5=60(千米),故④正确;
出发2小时,小货车离终点还有120﹣40×2=40(千米),故⑤错误;
故选:C.
7.解:由图象知:
A.甲车的平均速度为=60km/h,故A选项不合题意;
B.乙车的平均速度为=100km/h,故B选项不合题意;
C.甲10时到达B城,乙9时到达B城,所以乙比甲先到B城,故C选项不合题意;
D.甲5时出发,乙6时出发,所以乙比甲晚出发1h,故此选项错误,
故选:D.
8.解:由图象可得,
乙先到达终点,故选项A错误;
甲的速度为:1500÷5=300(米/分),故当跑到两分钟时,两人相距300×2﹣400=200(米),故选项B正确;
甲的速度保持不变,故选项C错误;
起跑两分钟后,乙的速度大于甲的速度,故选项D错误;
故选:B.
9.解:∵小甬的跑步速度比小真快,
∴小甬的图象经过原点,
设小真跑步路程y(米)和跑步时间x(分)之间的关系式为y=kx+200,则800=4k+200,解得k=150,
∴小真跑步路程y(米)和跑步时间x(分)之间的关系式为y=150x+200,
150×2+200=500,
∴小甬的图象经过(2,500),
∴小甬路程y(米)和跑步时间x(分)之间的关系式为y=250x,
∴小甬的速度:小真的速度=250:150,
∴小甬每跑100米时,小真只能跑60米.
故选:B.
10.解:读图可得,在x=40时,速度为0,故(1)正确;
AB段,y的值相等,故速度不变,故(2)正确;
x=30时,y=80,即在第30分钟时,汽车的速度是80千米/时;故(3)错误;
汽车共加速行驶的时间为:5+(15﹣10)=10(分钟),故(4)正确.
综上可得(1)(2)(4)正确,共3个.
故选:C.
11.解:①由题可得,A,B两城相距300千米,故①正确;
②由图可得,乙车比甲车晚出发1小时,却早到1小时,故②正确;
③甲车的平均速度为300÷(10﹣5)=60(km/h),乙车的平均速度为300÷(9﹣6)=100(km/h),所以甲车的平均速度比乙车的平均速度每小时慢40千米故③正确;
④相遇前:60(t﹣5)﹣100(t﹣6)=20,解得t=7;
相遇后:100(t﹣6)﹣60(t﹣5)=20,解得t=8.
当乙到底B城后,5+(300﹣20)÷60=;
即当甲、乙两车相距20千米时,t=7或8或.
故④错误.
即正的结论个数为3个.
故选:C.
12.解:由图象可得,
第4min时,容器内的水量为20L,故选项A正确;
每min进水量为:20÷4=5(L),故选项B正确;
每min出水量为:5﹣(30﹣20)÷(12﹣4)=3.75(L),故选项C错误;
第8min时,容器内的水量为:20+(8﹣4)×(5﹣3.75)=25(L),故选项D正确;
故选:C.
13.解:如图,等腰三角形ABC中,AB=AC,记AB=x,周长为y,
设BC=z,则y=2x+z,x>0,z>0.
①∵BC=z>0,
∴y=2x+z>2x,
∴对于任意等腰三角形ABC,其坐标位于直线y=2x的上方,不可能位于区域Ⅰ中,故结论①正确;
②∵三角形任意两边之和大于第三边,
∴2x>z,即z<2x,
∴y=2x+z<4x,
∴对于任意等腰三角形ABC,其坐标位于直线y=4x的下方,不可能位于区域Ⅳ中,故结论②错误;
③若三角形ABC是等腰直角三角形,则z=x,
∵1<<2,AB=x>0,
∴x<x<2x,
∴3x<2x+x<4x,
即3x<y<4x,
∴若三角形ABC是等腰直角三角形,其坐标位于区域Ⅲ中,故结论③正确;
④由图可知,点M位于区域Ⅲ中,此时3x<y<4x,
∴3x<2x+z<4x,
∴x<z<2x;
点N位于区域Ⅱ中,此时2x<y<3x,
∴2x<2x+z<3x,
∴0<z<x;
∴图中点M所对应等腰三角形的底边比点N所对应等腰三角形的底边长,故结论④正确.
故选:B.
14.解:∵直线y=﹣x+6分别与x、y轴交于点A、B,
∴点A(8,0),点B(0,6),
∴OA=8,OB=6,
∴AB===10,故①正确;
∵线段OB沿BC翻折,点O落在AB边上的点D处,
∴OB=BD=6,OC=CD,∠BOC=∠BDC=90°,
∴AD=AB﹣BD=4,
∵AC2=AD2+CD2,
∴(8﹣OC)2=16+OC2,
∴OC=3,
∴点C(3,0),
设直线BC解析式为:y=kx+6,
∴0=3k+6,
∴k=﹣2,
∴直线BC解析式为:y=﹣2x+6,故②正确;
如图,过点D作DH⊥AC于H,
∵CD=OC=3,
∴CA=5,
∵S△ACD=AC×DH=CD×AD,
∴DH==,
∴当y=时,=﹣x+6,
∴x=,
∴点D(,),故③正确;
∵线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,且OC=CD,
∴PD∥OC,
∴点P纵坐标为,故④错误,
故选:B.
15.解:∵直线y=﹣x+4与x轴交于点A,与y轴交于点B,
∴B(0,4),A(4,0),
∵点C是AB的中点,
∴C(2,2),
①当一边CD经过点O时,点F的坐标为(0,2),此时点F、B、C三点的圆心为BC的中点,坐标为(1,3);
②当直线CD过点G时,如图
取OB的中点N,连接CN,OC,则CN=ON=2,
∴OC=2,
∵G(﹣2,0),
∴直线GC的解析式为:y=x+1,
∴直线GC与y轴交点M(0,1),
过点M作MH⊥OC,
∵∠MOH=45,
∴MH=OH=,
∴CH=OC﹣OH=,
∵∠NCO=∠FCG=45°,
∴∠FCN=∠MCH,
又∵∠FNC=∠MHC,
∴△FNC∽△MHC,
∴,即,
得FN=,
∴OF=2+=.
∴F(,0),
此时过点F、B、C三点的圆心在BF的垂直平分线上,设圆心坐标为(x,),
则,
解得x=,
当∠ECD旋转过程中,射线CD与x轴的交点由点O到点G的过程中,则经过点B、C、F三点的圆的圆心所经过的路径为线段,
即由BC的中点到点(,),
∴所经过的路径长==.
故选:A.
二.填空题
16.解:由题意可得,
轿车的速度为:360÷2﹣60=120(km/h),
则点E的横坐标为:360÷120=3,纵坐标为:60×(3﹣2)+120×(3﹣2)=180,
故点E的坐标为(3,180),
故答案为:(3,180).
17.解:设甲开始的速度为a(m/min),则甲后来的速度为2a(m/min),
由题意可得,9+,
解得,a=500,
设乙的速度为b(m/min),由甲乙相遇知,
(9﹣)b+2a?1=(9﹣1)a,
∴b=1000,
∴甲乙相遇时乙距公司的路程为:(9﹣)×1000=3000,
甲到达小区的时间为:=12(min),
∴甲到小区时,乙距公司的路程为:3000﹣1000××(12﹣9)=1500(m),
故答案为:1500.
18.解:由图可得,
乙队的速度为300÷100=3(米/秒),
设甲队开始的速度为a米/秒,
15(3﹣a)=(45﹣15)×[a(1+)﹣3],
解得a=2,
∴甲队提速后的速度为2×(1+)=3.5(米/秒),
∴甲队到达终点用的时间为:15+(300﹣15×2)÷3.5=15+=15+77=92(秒),
∴甲队到达终点时,乙队离终点还有3×(100﹣92)=3×7=3×=(米),
故答案为:.
19.解:由题意可得,
李莉的速度为:(1500﹣1300)÷4=50(米/分),
王芳的速度为:(1300﹣390)÷(11﹣4)﹣50=80(米/分),
王芳、李莉相遇时的时间为:1300÷(50+80)+4=14(分钟),
∴李莉距离B地的路程为:50×14=700(米),
∵王芳到达B地时间的时间为:1300÷80+2=(分),
∴王芳到达B地时,李莉与B地相距的路程是:700×2﹣50×﹣200=287.5(米),
故答案为:287.5.
20.解:∵t=﹣kh+s,某时刻离地面200m处的气温t为8.4℃,离地面600m处的气温t为6℃,
∴,
解得,
∴t=﹣0.006h+9.6,
当h=1500时,t=﹣0.006×1500+9.6=0.6,
即此时天目山主峰的气温约为0.6℃,
故答案为:0.6℃.
21.解:根据题意结合图象可知小A在第1到第3分钟的速度为:(米/分),
∴两个机器人第一次相遇时间是在:1+=2(分钟),故①正确;
小B的速度为:80÷2=40(米/分),故②错误;
小A第3分钟后的速度为:(米/分),
∴赛程总长:100+80=180(米),故③错误;
180﹣40×4=20(米),
即小A到达终点的时候小B距离终点还有20米,故④正确.
综上所述,正确的有①④.
故答案为:①④
22.解:的速度为:3000÷20=150(米/分),
小熙的速度为:3000÷30=100(米/分),
小夏返回到小区的时间为:3000×2÷150=40(分),
在小夏返回到小区时,小熙走的总路程为:100×40=4000(米),
∴小夏返回到小区时,小熙距小区的路程为:3000×2﹣4000=2000(米).
故答案为:2000.
23.解:爸爸的速度为:1000×2÷20=100(米/分钟),
v1=1000÷20+100=150(米/分钟),
v2=1000÷10+100=200(米/分钟),
∴=.
故答案为:.
24.解:当x=0时,y=2x+4=4,
∴A(0,4);
当y=2x+4=0时,x=﹣2,
∴C(﹣2,0).
∴OA=4,OC=2,
∴AC==2.
如图所示,过点B作BD⊥x轴于点D.
∵∠ACO+∠ACB+∠BCD=180°,∠ACO+∠CAO=90°,∠ACB=90°,
∴∠CAO=∠BCD.
在△AOC和△CDB中,,
∴△AOC≌△CDB(AAS),
∴CD=AO=4,DB=OC=2,
OD=OC+CD=6,
∴点B的坐标为(﹣6,2).
如图所示.取AC的中点E,连接BE,OE,OB,
∵∠AOC=90°,AC=2,
∴OE=CE=AC=,
∵BC⊥AC,BC=2,
∴BE==5,
若点O,E,B不在一条直线上,则OB<OE+BE=5+.
若点O,E,B在一条直线上,则OB=OE+BE=5+,
∴当O,E,B三点在一条直线上时,OB取得最大值,最大值为5+,
故答案为:5+.
25.解:(1)∵由,得,
∴C(2,2);
(2)如图1,当∠CQO=90°,CQ=OQ,
∵C(2,2),
∴OQ=CQ=2,
∴t=2,
②如图2,当∠OCQ=90°,OC=CQ,
过C作CM⊥OA于M,
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴t=2+2=4,
即t的值为2或4,
故答案为:2或4;
(3)令﹣x+3=0,得x=6,由题意:Q(3,0),
设直线CQ的解析式是y=kx+b,
把C(2,2),Q(3,0)代入得:,
解得:k=﹣2,b=6,
∴直线CQ对应的函数关系式为:y=﹣2x+6.
故答案为:(1)(2,2);(3)y=﹣2x+6.
三.解答题
26.解:(1)根据函数的定义:距离地面高度是自变量,所在位置的温度是因变量,
故答案为:距离地面高度,所在位置的温度;
(2)由题意得:y=20﹣6h,
当x=5时,y=﹣10,
故答案为:y=20﹣6h,﹣10;
(3)从图象上看,h=2时,持续的时间为2分钟,
即返回途中飞机在2千米高空水平大约盘旋了2分钟;
故答案为:2;
(4)当h=2时,y=20﹣12=8,
即飞机发生事故时所在高空的温度是8度,
故答案为:8度.
27.解:(1)设y与x之间的函数关系式为y=kx+b,根据题意得:
,
解得,
∴y与x之间的函数关系式为y=﹣90x+270(0≤x≤2);
(2)把x=2代入y=﹣90x+270,得y=﹣180+270=90,
从A服务区到家的时间为:90÷60=1.5(小时),
2.5+1.5=4(小时),
答:小蕾从外婆家回到自己家共用了4小时.
28.解:(1)根据题意,每行程x千米,耗油0.1x升,即总油量减少0.1x升,
则油箱中的油剩下(50﹣0.1x)升,
∴y与x的函数关系式为:y=50﹣0.1x;
(2)当y=0时,50﹣0.1x=0,
解得x=500,
所以汽车最多可行驶500千米;
(3)当x=200时,代入x,y的关系式:
y=50﹣0.1×200=30.
所以,汽车行驶200km时,油桶中还有30升汽油;
(4)因为x代表的实际意义为行驶里程,所以x不能为负数,即x≥0;
又行驶中的耗油量为0.1x,不能超过油箱中现有汽油量的值50,
即0.1x≤50,
解得,x≤500.
综上所述,自变量x的取值范围是0≤x≤500.
29.解:(1)对于y=﹣x﹣2,令x=0,则y=﹣2,故点B(0,﹣2),
设直线AB的表达式为y=kx+b,则,解得,
故直线AB的表达式为y=x﹣2;
(2)连接OC,
则△ABC的面积=S四边形OBCA﹣S△AOB=×OB×xC+AO×|yC|﹣×AO×OB=13,
即×2×xC+×6×(﹣yC)﹣×2×6=13,
即﹣3yC+xC=19①,
而yC=﹣xC﹣2②,
联立①②并解得,即点C(4,﹣5);
(3)作点C关于x轴的对称点C′(4,5),将点C′向左平移2个单位得到点C″(2,5),
连接BC″交x轴于点M,将点M向右平移2个单位得到点N,则点M、N为所求点,此时四边形BMNC周长最小,
理由:∵MN∥C″C′且MN=C″C′,故四边形MNC′C″为平行四边形,
故C′N=C″M=CN,
则四边形BMNC周长=MN+BM+BC+CN=MN+BM+BC+C′N=MN+BM+BC+C″M=CB+MN+BC″为最小,
由点B、C″的坐标得,直线BC″的表达式为y=x﹣2,
令y=0,即y=x﹣2=0,解得x=,
故点M、N的坐标分别为(,0)、(,0).
30.解:(1)设直线DE的解析式为:y=kx+b,
∵顶点B的坐标为(4,2),E为AB的中点,
∴点E的坐标为:(4,1),
∵D(6,0),
则,解得,
∴直线DE的函数关系式为:y=﹣x+3;
(2)∵点F的纵坐标为2,且点F在直线DE上,
∴﹣x+3=2,
解得:x=2,
∴点F的坐标为(2,2);
∵函数y=mx﹣1的图象经过点F,
∴2m﹣1=2,
解得:m=;
(3)如图:设直线FH交y轴于点K,
对于y=x﹣1,
当y=0时,x﹣1=0,解得x=,即H(,0),
令x=0,则y=﹣1,则点K(0,﹣1);
同理可得,点G(0,3),则KG=4,
四边形OHFG的面积=S△GKF﹣S△OHK=×4×2﹣×1×=.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
