北师大版八年级数学上册《7.4 平行线的性质》 同步练习(word解析版)
文档属性
| 名称 | 北师大版八年级数学上册《7.4 平行线的性质》 同步练习(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 209.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 18:50:14 | ||
图片预览




文档简介
7.4
平行线的性质
一.选择题
1.如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点作GP∥AB.则下列结论:
①∠AMF与∠DNF是同旁内角;
②∠PGM=∠DNF;
③∠BMN+∠GHN=90°;
④∠AMG+∠CHG=270°.
其中正确结论的个数是( )
A.1个
B.2
个
C.3个
D.4个
2.如图,AC∥BD,AE平分∠BAC交BD于点E,若∠1=64°,则∠2=( )
A.116°
B.122°
C.128°
D.142°
3.如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.
A.70
B.150
C.90
D.100
4.如图,∠DAC+∠ACB=180°,EF∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是( )
A.10°
B.20°
C.15°
D.30°
5.如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=43°,那么∠2的度数是( )
A.48°
B.107°
C.92°
D.73°
6.小明将含30°的三角板和一把直尺如图放置,测得∠1=25°,则∠2的度数是( )
A.25°
B.30°
C.35°
D.40°
7.如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=60°,则∠2的度数为( )
A.60°
B.40°
C.30°
D.20°
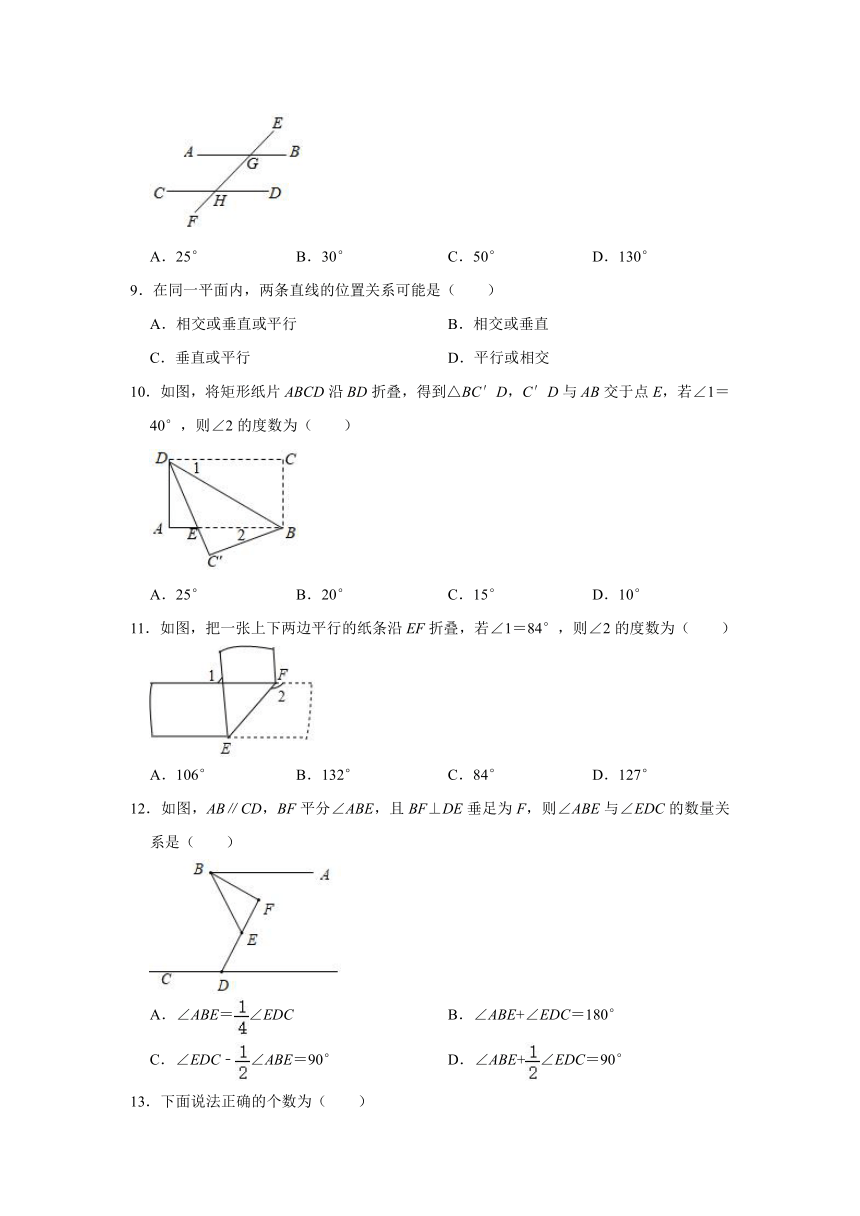
8.如图,AB∥CD,∠EGB=50°,∠CHF=( )
A.25°
B.30°
C.50°
D.130°
9.在同一平面内,两条直线的位置关系可能是( )
A.相交或垂直或平行
B.相交或垂直
C.垂直或平行
D.平行或相交
10.如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E,若∠1=40°,则∠2的度数为( )
A.25°
B.20°
C.15°
D.10°
11.如图,把一张上下两边平行的纸条沿EF折叠,若∠1=84°,则∠2的度数为( )
A.106°
B.132°
C.84°
D.127°
12.如图,AB∥CD,BF平分∠ABE,且BF⊥DE垂足为F,则∠ABE与∠EDC的数量关系是( )
A.∠ABE=∠EDC
B.∠ABE+∠EDC=180°
C.∠EDC﹣∠ABE=90°
D.∠ABE+∠EDC=90°
13.下面说法正确的个数为( )
①过直线外一点有且只有一条直线与已知直线平行
②两直线被第三条直线所截,同旁内角互补
③两角之和为180°,则这两个角一定是邻补角
④画一条线段的垂线段可以画无数条
A.1个
B.2个
C.3个
D.4个
14.如图,直线a∥b,点C在直线b上,∠ACB=90°,则( )
A.∠A=∠1+∠2
B.∠2+∠3+∠A=180°
C.∠1+∠2=90°
D.∠1+∠2+∠3=180°
15.下列说法正确的有( )
①平面内,不相交的两条直线是平行线;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平面内,过一点有且只有一条直线与已知直线平行;
④相等的角是对顶角;
⑤两角之和为180°,这两个角一定邻补角;
⑥P是直线a外一点,A、B、C分别是a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定是1.
A.1个
B.2个
C.3个
D.4个
二.填空题
16.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=36°,那么∠2的度数是
.
17.如图,直线AB∥CD,∠A=60°,∠D=40°,则∠E=
.
18.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=
.
19.如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为
.
20.如图,D为△ABC中BA延长线上一点,AE∥BC,若∠1=∠2,∠BAC=36°,则∠B=
°.
21.如图,AB∥CD,CB平分∠ABD,若∠ABC=40°,则∠D的度数为
.
22.如图,AB∥CD,∠A=50°,则∠1=
.
23.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD=
.
24.如图,已知点C为两条相互平行的直线AB,ED之间一点,∠ABC和∠CDE的角平分线相交于F,若∠BCD=∠BFD+10°,则∠BCD的度数为
.
25.如图,如果∠1=∠3,∠2=64°,那么∠4的度数为
.
三.解答题
26.问题情境
(1)如图1,已知AB∥CD,∠PBA=125°,∠PCD=155°,求∠BPC的度数.
佩佩同学的思路:过点P作PG∥AB,进而PG∥CD,由平行线的性质来求∠BPC,求得∠BPC=
°;
问题迁移
(2)图2,图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合,∠ACB=90°,DF∥CG,AB与FD相交于点E,有一动点P在边BC上运动,连接PE,PA,记∠PED=∠α,∠PAC=∠β.
①如图2,当点P在C,D两点之间运动时,请直接写出∠APE与∠α,∠β之间的数量关系;
②如图3,当点P在B,D两点之间运动时,∠APE与∠α,∠β之间有何数量关系?请判断并说明理由.
27.综合与探究
问题情境
在综合实践课上,老师组织七年级(2)班的同学开展了探究两角之间数量关系的数学活动,如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
探索发现
“快乐小组”经过探索后发现:
(1)当∠A=60°时,∠CBD=∠A.请说明理由.
(2)不断改变∠A的度数,∠CBD与∠A却始终存在某种数量关系,用含∠A的式子表示∠CBD为
.
操作探究
(3)“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变,请写出它们的关系,并说明理由.
(4)点P继续在射线AM上运动,当运动到使∠ACB=∠ABD时,请直接写出2∠ABC+∠A的结果.
28.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=(
),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴
=∠CDE(
),
∠DCE=∠BEF(
),
∴
=
(等量代换),
∴EF平分∠DEB(
).
29.完成下面推理过程.
如图:已知,∠A=112°,∠ABC=68°,BD⊥DC于点D,EF⊥DC于点F,求证:∠1=∠2.
证明:∵∠A=112°,∠ABC=68°(已知)
∴∠A+∠ABC=180°
∴AD∥BC(
)
∴∠1=
(
)
∵BD⊥DC,EF⊥DC(已知)
∴∠BDF=90°,∠EFC=90°(
)
∴∠BDF=∠EFC=90°
∴BD∥EF(
)
∴∠2=
(
)
∴∠1=∠2(
)
30.如图:已知,∠HCO=∠EBC,∠BHC+∠BEF=180°.
(1)求证:EF∥BH;
(2)若BH平分∠EBO,EF⊥AO于F,∠HCO=64°,求∠CHO的度数.
参考答案
一.选择题
1.解:∵∠AMF与∠DNF不是同旁内角,
∴①错误;
∵AB∥CD,GP∥AB,
∴AB∥CD∥GP,
∴∠PGM=∠CNM=∠DNF,∠BMN=∠HNG,∠AMN+∠HNG=180°,故②正确;
∵HG⊥MN,
∴∠HNG+∠GHN=90°,
∴∠BMN+∠GHN=90°,故③正确;
∵∠CHG=∠MNH+∠HGN,
∴∠MNH=∠CHG﹣90°,
∴∠AMN+∠HNG=∠AMN+∠CHG﹣90°=180°,
∴∠AMG+∠CHG=270°,故④正确,
故选:C.
2.解:∵∠1=64°,
∴∠3+∠4=180°﹣64°=116°,
∵AE平分∠BAC,
∴∠3=∠4=116°÷2=58°,
∵AC∥BD,
∴∠2+∠4=180°,
∴∠2=180°﹣58°=122°.
故选:B.
3.解:如图,延长AE交CD于点F,
∵AB∥CD,
∴∠BAE+∠EFC=180°,
又∵∠BAE=120°,
∴∠EFC=180°﹣∠BAE=180°﹣120°=60°,
又∵∠DCE=30°,
∴∠AEC=∠DCE+∠EFC=30°+60°=90°.
故选:C.
4.解:设∠BCE=∠ECF=∠BCF=x,
∵∠DAC=3∠BCF,
∴∠DAC=6x,
∵∠DAC+∠ACB=180°,
∴6x+x+x+20°=180°,
解得x=20°,
所以,∠FEC的度数为20°.
故选:B.
5.解:∵将一块含有30°的直角三角板的顶点放在直尺的一边上,∠1=43°,
∴∠2=∠3=180°﹣43°﹣30°=107°.
故选:B.
6.解:如图:
∵∠1=25°,∠3=∠1+30°,
∴∠3=55°,
∵直尺的对边平行,
∴∠4=∠3=55°,
∴∠2=180°﹣90°﹣∠4=180°﹣90°﹣55°=35°,
故选:C.
7.解:∵a∥b,
∴∠1+∠2+∠BAC=180°,
∵∠ABC=90°,∠1=60°,
∴∠2=30°,
故选:C.
8.解:∵AB∥CD,∠EGB=50°,
∴∠EHD=∠EGB=50°,
∴∠CHF=∠EHD=50°.
故选:C.
9.解:在同一个平面内,两条直线只有两种位置关系,即平行或相交.
故选:D.
10.解:在矩形ABCD中,∠C=90°,AB∥CD,
∴∠1+∠CBD=90°,CD∥AB,
∵∠1=40°,
∴∠CBD=50°,∠ABD=∠1=40°,
由折叠可知:∠2+∠ABD=∠CBD,
∴∠2+∠ABD=50°,
∴∠2=10°.
故选:D.
11.解:如图,
∵AF∥BE,
∴∠1=∠4=84°,
∵把一张上下两边平行的纸条沿EF折叠,
∴∠3=∠AEF==48°,
∵AF∥BE,
∴∠3+∠2=180°,
∴∠2=180°﹣48°=132°,
故选:B.
12.解:过F点作FG∥AB,
∵AB∥CD,
∴FG∥CD,
∴∠BFG=∠ABF,∠DFG+∠CDF=180°,
∵BF⊥DE,
∴∠BFD=90°,
∵BF平分∠ABE,
∴∠ABE=2∠ABF,
∴∠BFG+∠DFG+∠CDF=∠ABF+180°,
∴90°+∠CDE=∠ABE+180°,即∠EDC﹣∠ABE=90°.
故选:C.
13.解:①过直线外一点有且只有一条直线与已知直线平行,故此选项正确;
②两条平行的直线被第三条直线所截,同旁内角互补,故此选项错误;
③两角之和为180°,则这两个角互补,不一定是邻补角,故此选项错误;
④在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,经过的点不确定,可以画无数条,故此选项正确;
综上所述,正确的个数有2个,
故选:B.
14.解:∵a∥b,
∴∠4+∠ACB+∠2=180°,
∵∠ACB=90°,
∴∠4+∠2=90°,
∵∠4=∠1,
∴∠1+∠2=90°.
故选:C.
15.解:①根据平行线的定义,平面内,不相交的两条直线是平行线,故本选项正确;
②平面内,过一点有且只有一条直线与已知直线垂直,故本选项正确正确;
③平面内,过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
④相等的角不一定是对顶角,故本选项错误;
⑤两角之和为180°,则这两个角互为补角,但不一定是邻补角;故本选项错误;
⑥P是直线l外一点,A,B,C分别是l上的三点,已知PA=1,PB=2,PC=3,则点P到l的距离不大于1.故此选项错误.
综上所述,正确的有2个,
故选:B.
二.填空题
16.解:∵AB∥CD,
∴∠2=∠3,
∵∠1=36°,∠1+∠3=90°,
∴∠3=54°,
∴∠2=54°,
故答案为:54°.
17.解:∵AB∥CD,∠A=60°,
∴∠A=∠1=60°,
∵∠1=∠E+∠D,∠D=40°,
∴∠E=∠1﹣∠D=60°﹣40°=20°,
故答案为:20°.
18.解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
19.解:过P1作P1G∥AB,可得P1G∥CD,如图,
∴∠BEP1=∠EP1G,∠GP1F=∠P1FD,
∵EP1、FP1分别为∠BEF与∠EFD的平分线,
∴∠BEP1=∠FEP1,∠EFP1=∠DFP1,
∵AB∥CD,
∴∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠DFP1)=180°,
∴∠BEP1+∠DFP1=90°,
∵∠BEP1、∠DFP1的平分线相交于点K1,
∴∠BEP2=∠P1EP2,∠P1FP2=∠DFP2,
∵∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠P1FD)=180°,
∴∠BEP1+∠P1FD=90°,即∠P1EP2+∠P1FP2=45°,
∴∠K1=180°﹣(∠P1EF+∠EFP1)﹣(∠P1EP2+∠P1FP2)=45°,
故答案为:45°.
20.解:∵∠BAC=36°,∠1+∠2+∠BAC=180°,
∴∠1+∠2=144°,
∵∠1=∠2,
∴∠1=∠2=72°,
∵AE∥BC,
∴∠1=∠B,
∴∠B=72°,
故答案为:72.
21.解:∵CB平分∠ABD,
∴∠ABD=2∠ABC=80°,
∵AB∥CD,
∴∠ABD+∠D=180°,
∴∠D=180°﹣80°=100°,
则∠D的度数为100°.
故答案为:100°.
22.解:如图:
∵AB∥CD,
∴∠A+∠2=180°,
∵∠A=50°,
∴∠1=∠2=180°﹣∠A=180°﹣50°=130°.
故答案为:130°.
23.解:∵AB∥CD,
∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,
∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠1+∠3=45°,
∵∠5=∠2+∠3,
∴∠5=∠1+∠3=45°,
即∠BFD=45°,
故答案为:45°.
24.解:∵∠ABC和∠CDE的角平分线相交于F,
∴∠EDA=∠ADC,∠CBE=∠ABE,
又∵AB∥ED,
∴∠EDF=∠DAB,∠DFE=∠ABF,
设∠EDF=∠DAB=x,∠DFE=∠ABF=y,
∴∠BFD=∠EDA+∠ADE=x+y,
在四边形BCDF中,∠FBC=x,∠ADC=y,∠BFD=x+y,
∴∠BCD=360°﹣2(x+y),
∵∠BCD=∠BFD+10°,
∴∠BFD=x+y=100°,
∴∠BCD=360°﹣2(x+y)=160°,
故答案为:160°.
25.解:∵∠1=∠3,
∴AB∥CD,
∴∠2=∠5,
∵∠2=64°,
∴∠5=64°,
∵∠5+∠4=180°,
∴∠4=116°,
故答案为:116°.
三.解答题
26.解:(1)过点P作PG∥AB,则PG∥CD,
由平行线的性质可得∠B+∠BPG=180°,∠C+∠CPG=180°,
又∵∠PBA=125°,∠PCD=155°,
∴∠BPC=360°﹣125°﹣155°=80°,
故答案为:80;
(2)①如图2,
∠APE与∠α,∠β之间的数量关系为∠APE=∠α+∠β;
②如图3,∠APE与∠α,∠β之间的数量关系为∠APE=∠β﹣∠α;理由:
过P作PQ∥DF,
∵DF∥CG,
∴PQ∥CG,
∴∠β=∠QPA,∠α=∠QPE,
∴∠APE=∠APQ﹣∠EPQ=∠β﹣∠α.
27.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°,
又∵∠A=60°,
∴∠ABN=180°﹣∠A=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN=60°,
∴∠CBD=∠A.
(2)∵BC,CD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°﹣∠A,
∴∠CBD=.
(3)∠APB=2∠ADB
理由如下:
∵BD分别平分∠PBN,
∴∠PBN=2∠NBD,
∵AM∥BN,
∴∠PBN=∠APB∠NBD=∠ADB,
∴∠APB=2∠ADB.
(4)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
∵BC,CD分别平分∠ABP和∠PBN,
∴2∠ABC=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴2∠ABC+∠A=(∠A+∠ABN)=×180°=90°.
28.证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=∠CDE(两直线平行,内错角相等),
∴∠DCE=∠CDE(
等量代换),
∵CD∥EF
(
已知
),
∴∠DEF=∠CDE(两直线平行,内错角相等),
∠DCE=∠FEB(两直线平行,同位角相等),
∴∠DEF=∠FEB(等量代换),
∴EF平分∠DEB(
角平分线的定义
).
故答案为:∠CDE;∠DEF;两直线平行,内错角相等;两直线平行,同位角相等;∠DEF;∠FEB;角平分线的定义.
29.证明:∵∠A=112°,∠ABC=68°(已知),
∴∠A+∠ABC=180°.
∴AD∥BC(同旁内角互补,两直线平行).
∴∠1=∠3
(两直线平行,内错角相等
).
∵BD⊥DC,EF⊥DC(已知),
∴∠BDF=90°,∠EFC=90°(垂直的定义).
∴∠BDF=∠EFC=90°.
∴BD∥EF(同位角相等,两直线平行).
∴∠2=∠3(两直线平行,同位角相等).
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;∠3;两直线平行,内错角相等;垂直的定义;
同位角相等,两直线平行;∠3;两直线平行,同位角相等;等量代换.
30.证明:(1)∵∠HCO=∠EBC,
∴EB∥HC.
∴∠EBH=∠CHB.
∵∠BHC+∠BEF=180°,
∴∠EBH+∠BEF=180°.
∴EF∥BH.
(2)∵∠HCO=∠EBC,
∴∠HCO=∠EBC=64°,
∵BH平分∠EBO,
∴∠EBH=∠CHB=∠EBC=32°.
∵EF⊥AO于F,EF∥BH,
∴∠BHA=90°.
∴∠FHC=∠BHA+∠CHB=122°.
∵∠CHO=180°﹣∠FHC
=180°﹣122°
=58°.
平行线的性质
一.选择题
1.如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点作GP∥AB.则下列结论:
①∠AMF与∠DNF是同旁内角;
②∠PGM=∠DNF;
③∠BMN+∠GHN=90°;
④∠AMG+∠CHG=270°.
其中正确结论的个数是( )
A.1个
B.2
个
C.3个
D.4个
2.如图,AC∥BD,AE平分∠BAC交BD于点E,若∠1=64°,则∠2=( )
A.116°
B.122°
C.128°
D.142°
3.如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.
A.70
B.150
C.90
D.100
4.如图,∠DAC+∠ACB=180°,EF∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是( )
A.10°
B.20°
C.15°
D.30°
5.如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=43°,那么∠2的度数是( )
A.48°
B.107°
C.92°
D.73°
6.小明将含30°的三角板和一把直尺如图放置,测得∠1=25°,则∠2的度数是( )
A.25°
B.30°
C.35°
D.40°
7.如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=60°,则∠2的度数为( )
A.60°
B.40°
C.30°
D.20°
8.如图,AB∥CD,∠EGB=50°,∠CHF=( )
A.25°
B.30°
C.50°
D.130°
9.在同一平面内,两条直线的位置关系可能是( )
A.相交或垂直或平行
B.相交或垂直
C.垂直或平行
D.平行或相交
10.如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E,若∠1=40°,则∠2的度数为( )
A.25°
B.20°
C.15°
D.10°
11.如图,把一张上下两边平行的纸条沿EF折叠,若∠1=84°,则∠2的度数为( )
A.106°
B.132°
C.84°
D.127°
12.如图,AB∥CD,BF平分∠ABE,且BF⊥DE垂足为F,则∠ABE与∠EDC的数量关系是( )
A.∠ABE=∠EDC
B.∠ABE+∠EDC=180°
C.∠EDC﹣∠ABE=90°
D.∠ABE+∠EDC=90°
13.下面说法正确的个数为( )
①过直线外一点有且只有一条直线与已知直线平行
②两直线被第三条直线所截,同旁内角互补
③两角之和为180°,则这两个角一定是邻补角
④画一条线段的垂线段可以画无数条
A.1个
B.2个
C.3个
D.4个
14.如图,直线a∥b,点C在直线b上,∠ACB=90°,则( )
A.∠A=∠1+∠2
B.∠2+∠3+∠A=180°
C.∠1+∠2=90°
D.∠1+∠2+∠3=180°
15.下列说法正确的有( )
①平面内,不相交的两条直线是平行线;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平面内,过一点有且只有一条直线与已知直线平行;
④相等的角是对顶角;
⑤两角之和为180°,这两个角一定邻补角;
⑥P是直线a外一点,A、B、C分别是a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定是1.
A.1个
B.2个
C.3个
D.4个
二.填空题
16.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=36°,那么∠2的度数是
.
17.如图,直线AB∥CD,∠A=60°,∠D=40°,则∠E=
.
18.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A=
.
19.如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE的两条平分线相交于点P1,∠BEP1与∠DFP1的两条平分线相交于点P2,则∠P2的度数为
.
20.如图,D为△ABC中BA延长线上一点,AE∥BC,若∠1=∠2,∠BAC=36°,则∠B=
°.
21.如图,AB∥CD,CB平分∠ABD,若∠ABC=40°,则∠D的度数为
.
22.如图,AB∥CD,∠A=50°,则∠1=
.
23.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD=
.
24.如图,已知点C为两条相互平行的直线AB,ED之间一点,∠ABC和∠CDE的角平分线相交于F,若∠BCD=∠BFD+10°,则∠BCD的度数为
.
25.如图,如果∠1=∠3,∠2=64°,那么∠4的度数为
.
三.解答题
26.问题情境
(1)如图1,已知AB∥CD,∠PBA=125°,∠PCD=155°,求∠BPC的度数.
佩佩同学的思路:过点P作PG∥AB,进而PG∥CD,由平行线的性质来求∠BPC,求得∠BPC=
°;
问题迁移
(2)图2,图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合,∠ACB=90°,DF∥CG,AB与FD相交于点E,有一动点P在边BC上运动,连接PE,PA,记∠PED=∠α,∠PAC=∠β.
①如图2,当点P在C,D两点之间运动时,请直接写出∠APE与∠α,∠β之间的数量关系;
②如图3,当点P在B,D两点之间运动时,∠APE与∠α,∠β之间有何数量关系?请判断并说明理由.
27.综合与探究
问题情境
在综合实践课上,老师组织七年级(2)班的同学开展了探究两角之间数量关系的数学活动,如图,已知射线AM∥BN,连接AB,点P是射线AM上的一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
探索发现
“快乐小组”经过探索后发现:
(1)当∠A=60°时,∠CBD=∠A.请说明理由.
(2)不断改变∠A的度数,∠CBD与∠A却始终存在某种数量关系,用含∠A的式子表示∠CBD为
.
操作探究
(3)“智慧小组”利用量角器量出∠APB和∠ADB的度数后,探究二者之间的数量关系.他们惊奇地发现,当点P在射线AM上运动时,无论点P在AM上的什么位置,∠APB与∠ADB之间的数量关系都保持不变,请写出它们的关系,并说明理由.
(4)点P继续在射线AM上运动,当运动到使∠ACB=∠ABD时,请直接写出2∠ABC+∠A的结果.
28.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=(
),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴
=∠CDE(
),
∠DCE=∠BEF(
),
∴
=
(等量代换),
∴EF平分∠DEB(
).
29.完成下面推理过程.
如图:已知,∠A=112°,∠ABC=68°,BD⊥DC于点D,EF⊥DC于点F,求证:∠1=∠2.
证明:∵∠A=112°,∠ABC=68°(已知)
∴∠A+∠ABC=180°
∴AD∥BC(
)
∴∠1=
(
)
∵BD⊥DC,EF⊥DC(已知)
∴∠BDF=90°,∠EFC=90°(
)
∴∠BDF=∠EFC=90°
∴BD∥EF(
)
∴∠2=
(
)
∴∠1=∠2(
)
30.如图:已知,∠HCO=∠EBC,∠BHC+∠BEF=180°.
(1)求证:EF∥BH;
(2)若BH平分∠EBO,EF⊥AO于F,∠HCO=64°,求∠CHO的度数.
参考答案
一.选择题
1.解:∵∠AMF与∠DNF不是同旁内角,
∴①错误;
∵AB∥CD,GP∥AB,
∴AB∥CD∥GP,
∴∠PGM=∠CNM=∠DNF,∠BMN=∠HNG,∠AMN+∠HNG=180°,故②正确;
∵HG⊥MN,
∴∠HNG+∠GHN=90°,
∴∠BMN+∠GHN=90°,故③正确;
∵∠CHG=∠MNH+∠HGN,
∴∠MNH=∠CHG﹣90°,
∴∠AMN+∠HNG=∠AMN+∠CHG﹣90°=180°,
∴∠AMG+∠CHG=270°,故④正确,
故选:C.
2.解:∵∠1=64°,
∴∠3+∠4=180°﹣64°=116°,
∵AE平分∠BAC,
∴∠3=∠4=116°÷2=58°,
∵AC∥BD,
∴∠2+∠4=180°,
∴∠2=180°﹣58°=122°.
故选:B.
3.解:如图,延长AE交CD于点F,
∵AB∥CD,
∴∠BAE+∠EFC=180°,
又∵∠BAE=120°,
∴∠EFC=180°﹣∠BAE=180°﹣120°=60°,
又∵∠DCE=30°,
∴∠AEC=∠DCE+∠EFC=30°+60°=90°.
故选:C.
4.解:设∠BCE=∠ECF=∠BCF=x,
∵∠DAC=3∠BCF,
∴∠DAC=6x,
∵∠DAC+∠ACB=180°,
∴6x+x+x+20°=180°,
解得x=20°,
所以,∠FEC的度数为20°.
故选:B.
5.解:∵将一块含有30°的直角三角板的顶点放在直尺的一边上,∠1=43°,
∴∠2=∠3=180°﹣43°﹣30°=107°.
故选:B.
6.解:如图:
∵∠1=25°,∠3=∠1+30°,
∴∠3=55°,
∵直尺的对边平行,
∴∠4=∠3=55°,
∴∠2=180°﹣90°﹣∠4=180°﹣90°﹣55°=35°,
故选:C.
7.解:∵a∥b,
∴∠1+∠2+∠BAC=180°,
∵∠ABC=90°,∠1=60°,
∴∠2=30°,
故选:C.
8.解:∵AB∥CD,∠EGB=50°,
∴∠EHD=∠EGB=50°,
∴∠CHF=∠EHD=50°.
故选:C.
9.解:在同一个平面内,两条直线只有两种位置关系,即平行或相交.
故选:D.
10.解:在矩形ABCD中,∠C=90°,AB∥CD,
∴∠1+∠CBD=90°,CD∥AB,
∵∠1=40°,
∴∠CBD=50°,∠ABD=∠1=40°,
由折叠可知:∠2+∠ABD=∠CBD,
∴∠2+∠ABD=50°,
∴∠2=10°.
故选:D.
11.解:如图,
∵AF∥BE,
∴∠1=∠4=84°,
∵把一张上下两边平行的纸条沿EF折叠,
∴∠3=∠AEF==48°,
∵AF∥BE,
∴∠3+∠2=180°,
∴∠2=180°﹣48°=132°,
故选:B.
12.解:过F点作FG∥AB,
∵AB∥CD,
∴FG∥CD,
∴∠BFG=∠ABF,∠DFG+∠CDF=180°,
∵BF⊥DE,
∴∠BFD=90°,
∵BF平分∠ABE,
∴∠ABE=2∠ABF,
∴∠BFG+∠DFG+∠CDF=∠ABF+180°,
∴90°+∠CDE=∠ABE+180°,即∠EDC﹣∠ABE=90°.
故选:C.
13.解:①过直线外一点有且只有一条直线与已知直线平行,故此选项正确;
②两条平行的直线被第三条直线所截,同旁内角互补,故此选项错误;
③两角之和为180°,则这两个角互补,不一定是邻补角,故此选项错误;
④在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,经过的点不确定,可以画无数条,故此选项正确;
综上所述,正确的个数有2个,
故选:B.
14.解:∵a∥b,
∴∠4+∠ACB+∠2=180°,
∵∠ACB=90°,
∴∠4+∠2=90°,
∵∠4=∠1,
∴∠1+∠2=90°.
故选:C.
15.解:①根据平行线的定义,平面内,不相交的两条直线是平行线,故本选项正确;
②平面内,过一点有且只有一条直线与已知直线垂直,故本选项正确正确;
③平面内,过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
④相等的角不一定是对顶角,故本选项错误;
⑤两角之和为180°,则这两个角互为补角,但不一定是邻补角;故本选项错误;
⑥P是直线l外一点,A,B,C分别是l上的三点,已知PA=1,PB=2,PC=3,则点P到l的距离不大于1.故此选项错误.
综上所述,正确的有2个,
故选:B.
二.填空题
16.解:∵AB∥CD,
∴∠2=∠3,
∵∠1=36°,∠1+∠3=90°,
∴∠3=54°,
∴∠2=54°,
故答案为:54°.
17.解:∵AB∥CD,∠A=60°,
∴∠A=∠1=60°,
∵∠1=∠E+∠D,∠D=40°,
∴∠E=∠1﹣∠D=60°﹣40°=20°,
故答案为:20°.
18.解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
19.解:过P1作P1G∥AB,可得P1G∥CD,如图,
∴∠BEP1=∠EP1G,∠GP1F=∠P1FD,
∵EP1、FP1分别为∠BEF与∠EFD的平分线,
∴∠BEP1=∠FEP1,∠EFP1=∠DFP1,
∵AB∥CD,
∴∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠DFP1)=180°,
∴∠BEP1+∠DFP1=90°,
∵∠BEP1、∠DFP1的平分线相交于点K1,
∴∠BEP2=∠P1EP2,∠P1FP2=∠DFP2,
∵∠BEP1+∠FEP1+∠EFP1+∠DFP1=180°,即2(∠BEP1+∠P1FD)=180°,
∴∠BEP1+∠P1FD=90°,即∠P1EP2+∠P1FP2=45°,
∴∠K1=180°﹣(∠P1EF+∠EFP1)﹣(∠P1EP2+∠P1FP2)=45°,
故答案为:45°.
20.解:∵∠BAC=36°,∠1+∠2+∠BAC=180°,
∴∠1+∠2=144°,
∵∠1=∠2,
∴∠1=∠2=72°,
∵AE∥BC,
∴∠1=∠B,
∴∠B=72°,
故答案为:72.
21.解:∵CB平分∠ABD,
∴∠ABD=2∠ABC=80°,
∵AB∥CD,
∴∠ABD+∠D=180°,
∴∠D=180°﹣80°=100°,
则∠D的度数为100°.
故答案为:100°.
22.解:如图:
∵AB∥CD,
∴∠A+∠2=180°,
∵∠A=50°,
∴∠1=∠2=180°﹣∠A=180°﹣50°=130°.
故答案为:130°.
23.解:∵AB∥CD,
∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,
∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠1+∠3=45°,
∵∠5=∠2+∠3,
∴∠5=∠1+∠3=45°,
即∠BFD=45°,
故答案为:45°.
24.解:∵∠ABC和∠CDE的角平分线相交于F,
∴∠EDA=∠ADC,∠CBE=∠ABE,
又∵AB∥ED,
∴∠EDF=∠DAB,∠DFE=∠ABF,
设∠EDF=∠DAB=x,∠DFE=∠ABF=y,
∴∠BFD=∠EDA+∠ADE=x+y,
在四边形BCDF中,∠FBC=x,∠ADC=y,∠BFD=x+y,
∴∠BCD=360°﹣2(x+y),
∵∠BCD=∠BFD+10°,
∴∠BFD=x+y=100°,
∴∠BCD=360°﹣2(x+y)=160°,
故答案为:160°.
25.解:∵∠1=∠3,
∴AB∥CD,
∴∠2=∠5,
∵∠2=64°,
∴∠5=64°,
∵∠5+∠4=180°,
∴∠4=116°,
故答案为:116°.
三.解答题
26.解:(1)过点P作PG∥AB,则PG∥CD,
由平行线的性质可得∠B+∠BPG=180°,∠C+∠CPG=180°,
又∵∠PBA=125°,∠PCD=155°,
∴∠BPC=360°﹣125°﹣155°=80°,
故答案为:80;
(2)①如图2,
∠APE与∠α,∠β之间的数量关系为∠APE=∠α+∠β;
②如图3,∠APE与∠α,∠β之间的数量关系为∠APE=∠β﹣∠α;理由:
过P作PQ∥DF,
∵DF∥CG,
∴PQ∥CG,
∴∠β=∠QPA,∠α=∠QPE,
∴∠APE=∠APQ﹣∠EPQ=∠β﹣∠α.
27.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°,
又∵∠A=60°,
∴∠ABN=180°﹣∠A=120°.
∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN=60°,
∴∠CBD=∠A.
(2)∵BC,CD分别平分∠ABP和∠PBN,
∴∠CBP=∠ABP,∠DBP=∠PBN,
∴∠CBD=∠CBP+∠DBP=∠ABP+∠PBN=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°﹣∠A,
∴∠CBD=.
(3)∠APB=2∠ADB
理由如下:
∵BD分别平分∠PBN,
∴∠PBN=2∠NBD,
∵AM∥BN,
∴∠PBN=∠APB∠NBD=∠ADB,
∴∠APB=2∠ADB.
(4)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
∵BC,CD分别平分∠ABP和∠PBN,
∴2∠ABC=∠ABN,
∵AM∥BN,
∴∠A+∠ABN=180°,
∴2∠ABC+∠A=(∠A+∠ABN)=×180°=90°.
28.证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=∠CDE(两直线平行,内错角相等),
∴∠DCE=∠CDE(
等量代换),
∵CD∥EF
(
已知
),
∴∠DEF=∠CDE(两直线平行,内错角相等),
∠DCE=∠FEB(两直线平行,同位角相等),
∴∠DEF=∠FEB(等量代换),
∴EF平分∠DEB(
角平分线的定义
).
故答案为:∠CDE;∠DEF;两直线平行,内错角相等;两直线平行,同位角相等;∠DEF;∠FEB;角平分线的定义.
29.证明:∵∠A=112°,∠ABC=68°(已知),
∴∠A+∠ABC=180°.
∴AD∥BC(同旁内角互补,两直线平行).
∴∠1=∠3
(两直线平行,内错角相等
).
∵BD⊥DC,EF⊥DC(已知),
∴∠BDF=90°,∠EFC=90°(垂直的定义).
∴∠BDF=∠EFC=90°.
∴BD∥EF(同位角相等,两直线平行).
∴∠2=∠3(两直线平行,同位角相等).
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;∠3;两直线平行,内错角相等;垂直的定义;
同位角相等,两直线平行;∠3;两直线平行,同位角相等;等量代换.
30.证明:(1)∵∠HCO=∠EBC,
∴EB∥HC.
∴∠EBH=∠CHB.
∵∠BHC+∠BEF=180°,
∴∠EBH+∠BEF=180°.
∴EF∥BH.
(2)∵∠HCO=∠EBC,
∴∠HCO=∠EBC=64°,
∵BH平分∠EBO,
∴∠EBH=∠CHB=∠EBC=32°.
∵EF⊥AO于F,EF∥BH,
∴∠BHA=90°.
∴∠FHC=∠BHA+∠CHB=122°.
∵∠CHO=180°﹣∠FHC
=180°﹣122°
=58°.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
