九年级数学直线与圆的关系复习课件
文档属性
| 名称 | 九年级数学直线与圆的关系复习课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 37.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-06 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
复习课
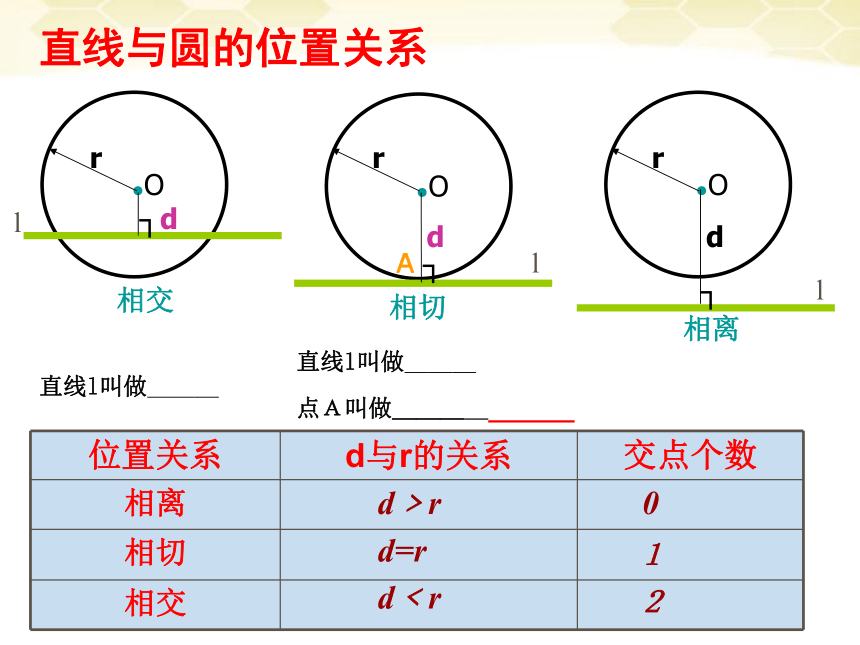
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
直线与圆的位置关系
位置关系 d与r的关系 交点个数
相离
相切
相交
l
l
l
A
直线l叫做___
直线l叫做___
点A叫做___
d﹥r
d=r
d﹤r
0
1
2
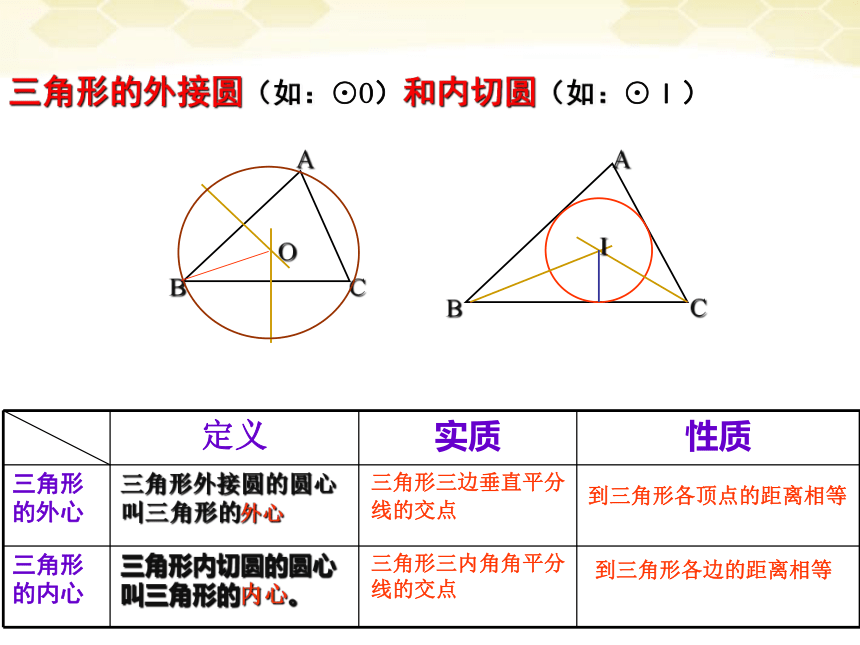
三角形的外接圆(如:⊙O)和内切圆(如:⊙I)
A
B
C
I
三角形内切圆的圆心叫三角形的内心。
三角形外接圆的圆心叫三角形的外心
A
B
C
O
定义 实质 性质
三角形的外心
三角形的内心
三角形三边垂直平分线的交点
三角形三内角角平分线的交点
到三角形各边的距离相等
到三角形各顶点的距离相等
1.已知⊙O的半径为5 cm,直线l上有一点Q且OQ =5cm,则直线l与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切 或相交
2.某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭的中心位置。
C
B
A
D
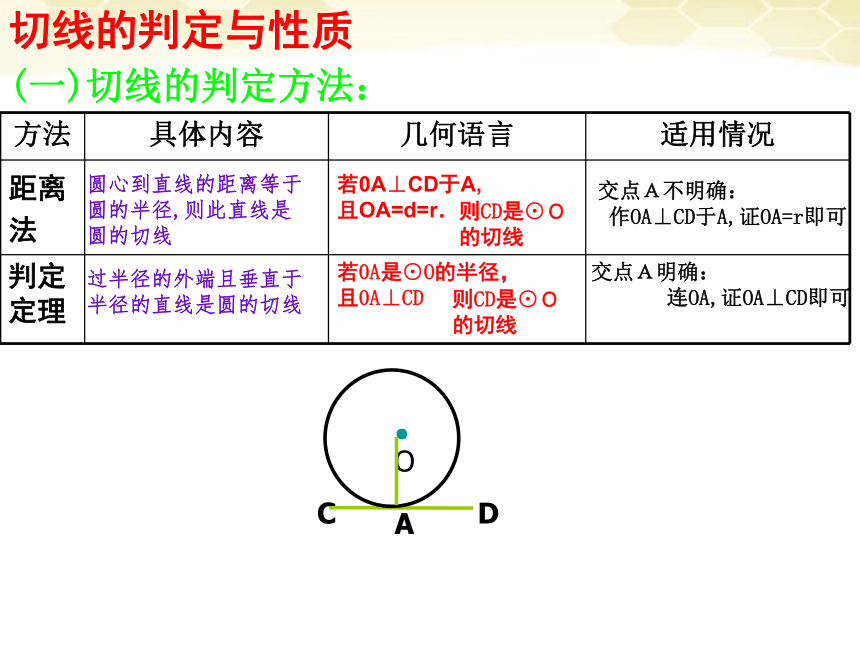
切线的判定与性质
(一)切线的判定方法:
C
D
●O
A
方法 具体内容 几何语言 适用情况
距离
法
判定
定理
圆心到直线的距离等于
圆的半径,则此直线是
圆的切线
过半径的外端且垂直于
半径的直线是圆的切线
若0A⊥CD于A,且OA=d=r.
则CD是⊙O
的切线
交点A明确:
连OA,证OA⊥CD即可
交点A不明确:
作OA⊥CD于A,证OA=r即可
若0A是⊙O的半径,
且0A⊥CD
则CD是⊙O
的切线
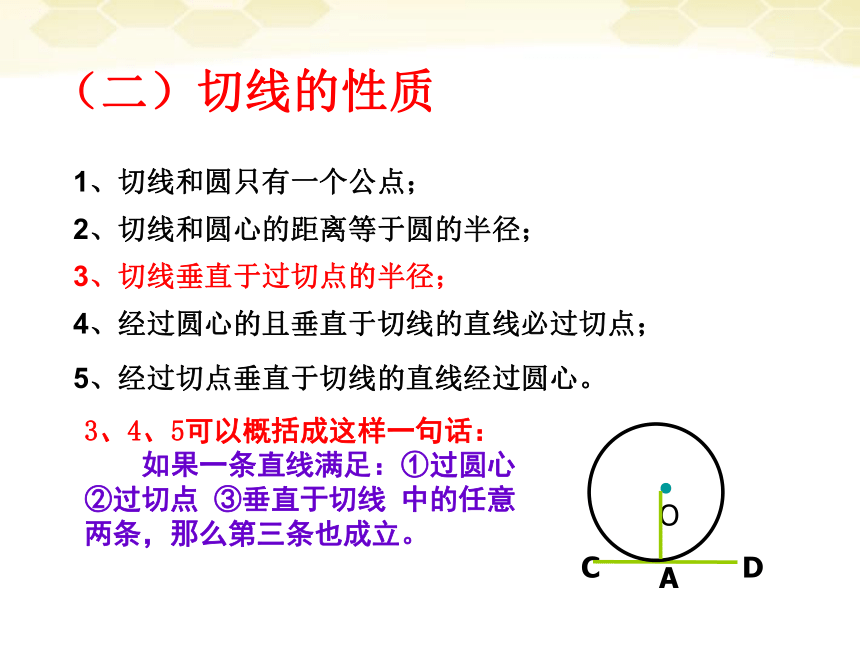
(二)切线的性质
1、切线和圆只有一个公点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心的且垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线经过圆心。
C
D
●O
A
3、4、5可以概括成这样一句话:
如果一条直线满足:①过圆心
②过切点 ③垂直于切线 中的任意
两条,那么第三条也成立。
1.如图1,△ABC中,AB=AC,O是BC的中点,以O为
圆心的圆与AB相切于点D,
求证:AC是圆的切线
2.如图2,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
(图1) (图2)
·
A
B
E
O
C
D
A
B
C
D
E
O
.
(距离法)
(判定定理)
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
A
B
P
●O
┗
┏
1
2
切线长定理
几何语言:若PA,PB切⊙O于A,B
则①PA=PB ②∠1=∠2
A
B
C
●
┗
┏
┓
O
D
E
F
┗
直角三角形的内切圆半径
与三边关系.
1.一个基本图形;
2.两个结论
(1)四边形OECF是正方形
(2)① r=(a+b-c) ÷2
② r=ab ÷(a+b+c)
3.两个方法
(1)代数法(方程思想)
(2)面积法
1.如图,圆O切PB于点B,PB=4,PA=2,则圆O的半径是____.
2.在直角三角形ABC中, ∠C=90度,AC=6,BC=8,则其外接圆半径=___, 内切圆半径=___.
A
P
B
3
5
2
O
例 如图4,⊙M与x轴相交于点A(2,0),
B(8,0),与y轴相切于点C,
求圆心M的坐标.
例题讲解
D
解:如图,AB=OB-OA=8-2=6,
过M作MD⊥AB于D,则AD=3,
∴OD=5,
连结CM则CM⊥OC,
∵CO⊥OD,
∴四边形ODMC是矩形,
∴MC=OD=5,
连结AM,则AM=MC=5
∴MD= =4
∴M(5,4)
练习题:
据报道 :我国探月“嫦娥计划”第一颗卫星“嫦娥一号”
已定于10 月24日发射.
听到这则新闻,大大激发了王坤同学爱好天文的热情.他通过上网查阅资料了解到.地球和金星的运行轨道可以近似地看着以太阳为圆心的同心圆,且这两个同心圆在同一平面上(如图所示).由于金星和地球运转速度不同,所以两者的位置不断地发生变化:
当金星,地球距离最近时,此时叫“下合”
当金星,地球距离最远时,此时叫“上合”
在地球上观察金星的视线恰好与金星轨道相切时,此时分别叫“东大距”和“西大距”.
已知地球与太阳相距约15(千万km),金星与太阳相距约10(千万km),
分别求“下合” ,“东大距”,“西大距”,“上合”时,金星与地球的距离.
(可用根号表示)
地球轨道
金星轨道
太阳
课 堂 小 结
复习课
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
直线与圆的位置关系
位置关系 d与r的关系 交点个数
相离
相切
相交
l
l
l
A
直线l叫做___
直线l叫做___
点A叫做___
d﹥r
d=r
d﹤r
0
1
2
三角形的外接圆(如:⊙O)和内切圆(如:⊙I)
A
B
C
I
三角形内切圆的圆心叫三角形的内心。
三角形外接圆的圆心叫三角形的外心
A
B
C
O
定义 实质 性质
三角形的外心
三角形的内心
三角形三边垂直平分线的交点
三角形三内角角平分线的交点
到三角形各边的距离相等
到三角形各顶点的距离相等
1.已知⊙O的半径为5 cm,直线l上有一点Q且OQ =5cm,则直线l与⊙O的位置关系是( )
A、相离 B、相切 C、相交 D、相切 或相交
2.某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭的中心位置。
C
B
A
D
切线的判定与性质
(一)切线的判定方法:
C
D
●O
A
方法 具体内容 几何语言 适用情况
距离
法
判定
定理
圆心到直线的距离等于
圆的半径,则此直线是
圆的切线
过半径的外端且垂直于
半径的直线是圆的切线
若0A⊥CD于A,且OA=d=r.
则CD是⊙O
的切线
交点A明确:
连OA,证OA⊥CD即可
交点A不明确:
作OA⊥CD于A,证OA=r即可
若0A是⊙O的半径,
且0A⊥CD
则CD是⊙O
的切线
(二)切线的性质
1、切线和圆只有一个公点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心的且垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线经过圆心。
C
D
●O
A
3、4、5可以概括成这样一句话:
如果一条直线满足:①过圆心
②过切点 ③垂直于切线 中的任意
两条,那么第三条也成立。
1.如图1,△ABC中,AB=AC,O是BC的中点,以O为
圆心的圆与AB相切于点D,
求证:AC是圆的切线
2.如图2,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.
(图1) (图2)
·
A
B
E
O
C
D
A
B
C
D
E
O
.
(距离法)
(判定定理)
从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.
A
B
P
●O
┗
┏
1
2
切线长定理
几何语言:若PA,PB切⊙O于A,B
则①PA=PB ②∠1=∠2
A
B
C
●
┗
┏
┓
O
D
E
F
┗
直角三角形的内切圆半径
与三边关系.
1.一个基本图形;
2.两个结论
(1)四边形OECF是正方形
(2)① r=(a+b-c) ÷2
② r=ab ÷(a+b+c)
3.两个方法
(1)代数法(方程思想)
(2)面积法
1.如图,圆O切PB于点B,PB=4,PA=2,则圆O的半径是____.
2.在直角三角形ABC中, ∠C=90度,AC=6,BC=8,则其外接圆半径=___, 内切圆半径=___.
A
P
B
3
5
2
O
例 如图4,⊙M与x轴相交于点A(2,0),
B(8,0),与y轴相切于点C,
求圆心M的坐标.
例题讲解
D
解:如图,AB=OB-OA=8-2=6,
过M作MD⊥AB于D,则AD=3,
∴OD=5,
连结CM则CM⊥OC,
∵CO⊥OD,
∴四边形ODMC是矩形,
∴MC=OD=5,
连结AM,则AM=MC=5
∴MD= =4
∴M(5,4)
练习题:
据报道 :我国探月“嫦娥计划”第一颗卫星“嫦娥一号”
已定于10 月24日发射.
听到这则新闻,大大激发了王坤同学爱好天文的热情.他通过上网查阅资料了解到.地球和金星的运行轨道可以近似地看着以太阳为圆心的同心圆,且这两个同心圆在同一平面上(如图所示).由于金星和地球运转速度不同,所以两者的位置不断地发生变化:
当金星,地球距离最近时,此时叫“下合”
当金星,地球距离最远时,此时叫“上合”
在地球上观察金星的视线恰好与金星轨道相切时,此时分别叫“东大距”和“西大距”.
已知地球与太阳相距约15(千万km),金星与太阳相距约10(千万km),
分别求“下合” ,“东大距”,“西大距”,“上合”时,金星与地球的距离.
(可用根号表示)
地球轨道
金星轨道
太阳
课 堂 小 结
同课章节目录
