八年级数学角的平分线的性质第一课时
文档属性
| 名称 | 八年级数学角的平分线的性质第一课时 |

|
|
| 格式 | rar | ||
| 文件大小 | 95.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-06 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
11.3 角的平分线的性质
托二中 赵晓玉
(第1课时)
学习目标:
1、掌握用尺规作已知角的平分线的方法。
2、掌握角平分线的性质并能初步运用。
3、在探究的过程中,培养我们探究问题的兴
趣,增强解决问题的信心;通过合作、交
流、讨论,增强我们合作、沟通的能力。
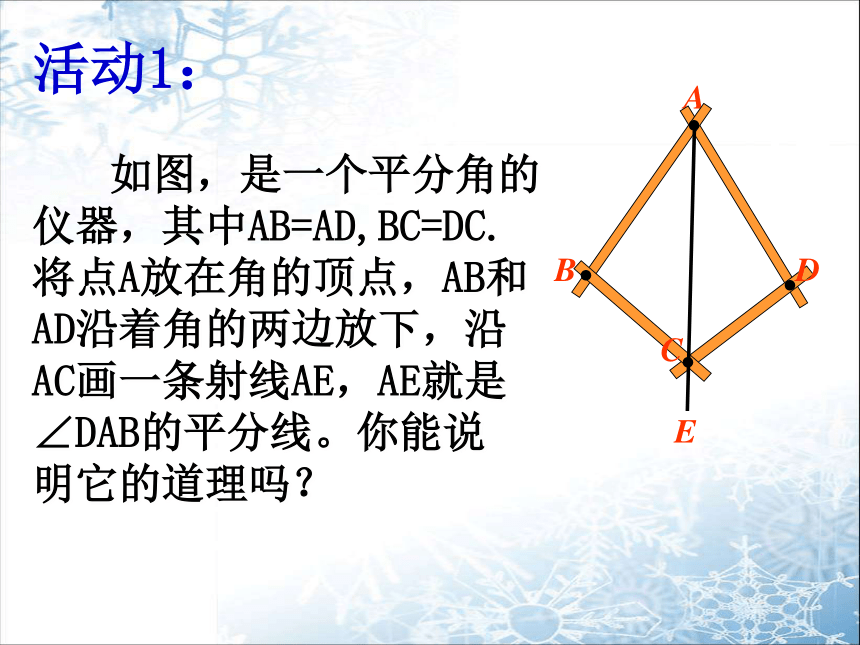
如图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线。你能说
明它的道理吗?
活动1:
B
A
·
·
·
·
E
D
C
活动2:
用尺子和圆规作角的平分线.
已知:∠AOB
求作: ∠AOB的平分线.
作法:
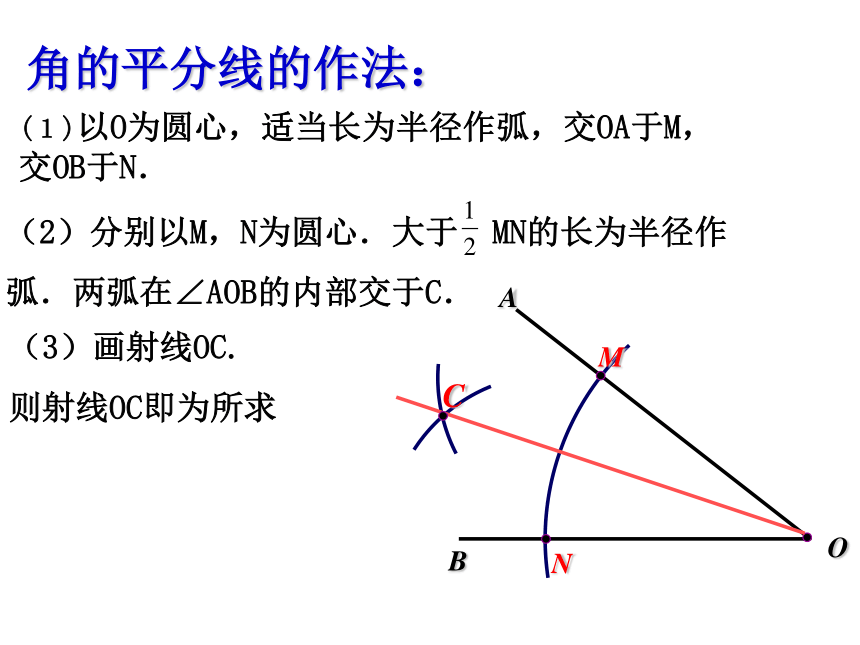
角的平分线的作法:
(3)画射线OC.
则射线OC即为所求
A
B
O
M
N
C
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
(2)分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
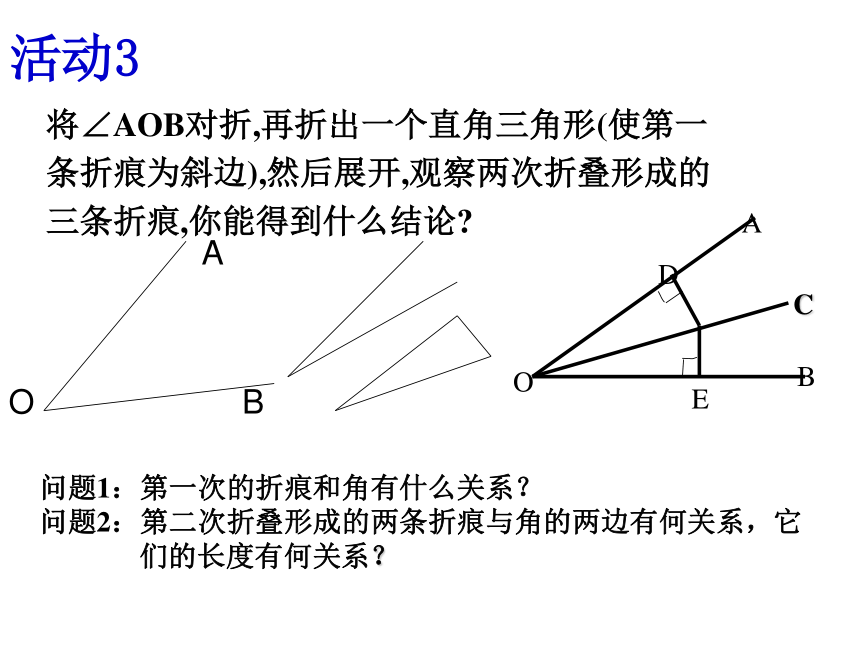
活动3
将∠AOB对折,再折出一个直角三角形(使第一
条折痕为斜边),然后展开,观察两次折叠形成的
三条折痕,你能得到什么结论
O
A
B
A
O
B
E
D
问题1:第一次的折痕和角有什么关系?
问题2:第二次折叠形成的两条折痕与角的两边有何关系,它
们的长度有何关系?
C
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
分析命题中的题设和结论,结合图形,用数学符号表示已知和求证。
E
D
O
A
B
P
C
题设:一个点在一个角的平分线上
结论:这个点到这个角两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
E
D
O
A
B
P
C
温故知新:
例:△ABC中,AD是∠BAC的平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:EB=FC.
A
B
C
D
E
F
相信自己!
证明:∵ AD平分∠BAC
DE⊥AB,DF⊥AC
∴ DE=DF (角的平分线上的点
到角的两边的距离相等)
在Rt△DEB和Rt△DFC中,
DE=DF
BD=CD
∴ Rt△DEB≌Rt△DFC (HL)
∴ EB=FC
:
辨析:
要在S区建立一个集贸市场,使它到公路、铁路的距离相等,小明工程师说这个集贸市场一定位于公路与铁路夹角的平分线上。(如图示)
火眼金睛
s
小结与收获:
布置作业:P19.练习
P22. 2
1、角的平分线的画法:(借助量角器、平分角的仪器等),但尺规画图最佳,这些画法的道理可以通过全等三角形的证明来获得.
2、角的平分线的性质:角的平分线上的点到
角两边的距离相等.
3、角的平分线的性质证明线段相等的新途径.
如图,△ABC的角平分线BM、CN相交于点。
求证:点P到三角形三边的距离都相等。
A
B
C
P
E
F
G
M
N
超越自己!(选做)
11.3 角的平分线的性质
托二中 赵晓玉
(第1课时)
学习目标:
1、掌握用尺规作已知角的平分线的方法。
2、掌握角平分线的性质并能初步运用。
3、在探究的过程中,培养我们探究问题的兴
趣,增强解决问题的信心;通过合作、交
流、讨论,增强我们合作、沟通的能力。
如图,是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线。你能说
明它的道理吗?
活动1:
B
A
·
·
·
·
E
D
C
活动2:
用尺子和圆规作角的平分线.
已知:∠AOB
求作: ∠AOB的平分线.
作法:
角的平分线的作法:
(3)画射线OC.
则射线OC即为所求
A
B
O
M
N
C
(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
(2)分别以M,N为圆心.大于 MN的长为半径作弧.两弧在∠AOB的内部交于C.
活动3
将∠AOB对折,再折出一个直角三角形(使第一
条折痕为斜边),然后展开,观察两次折叠形成的
三条折痕,你能得到什么结论
O
A
B
A
O
B
E
D
问题1:第一次的折痕和角有什么关系?
问题2:第二次折叠形成的两条折痕与角的两边有何关系,它
们的长度有何关系?
C
角的平分线的性质:角的平分线上的点到角的两边的距离相等.
分析命题中的题设和结论,结合图形,用数学符号表示已知和求证。
E
D
O
A
B
P
C
题设:一个点在一个角的平分线上
结论:这个点到这个角两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
E
D
O
A
B
P
C
温故知新:
例:△ABC中,AD是∠BAC的平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:EB=FC.
A
B
C
D
E
F
相信自己!
证明:∵ AD平分∠BAC
DE⊥AB,DF⊥AC
∴ DE=DF (角的平分线上的点
到角的两边的距离相等)
在Rt△DEB和Rt△DFC中,
DE=DF
BD=CD
∴ Rt△DEB≌Rt△DFC (HL)
∴ EB=FC
:
辨析:
要在S区建立一个集贸市场,使它到公路、铁路的距离相等,小明工程师说这个集贸市场一定位于公路与铁路夹角的平分线上。(如图示)
火眼金睛
s
小结与收获:
布置作业:P19.练习
P22. 2
1、角的平分线的画法:(借助量角器、平分角的仪器等),但尺规画图最佳,这些画法的道理可以通过全等三角形的证明来获得.
2、角的平分线的性质:角的平分线上的点到
角两边的距离相等.
3、角的平分线的性质证明线段相等的新途径.
如图,△ABC的角平分线BM、CN相交于点。
求证:点P到三角形三边的距离都相等。
A
B
C
P
E
F
G
M
N
超越自己!(选做)
