八年级数学矩形的性质
图片预览





文档简介
(共15张PPT)
19.2.1 矩形(1)
托县第二中学 赵晓玉
学习目标:
1、探索矩形的定义和矩形的性质.
2、会初步运用矩形的定义和性质来 解决简单问题.
3、培养学生的观察能力、动手能力、自学能力、计算能力和逻辑思维能力.
探究(一):
1、用自制的平行四边形,轻轻的推动其中的一点,你会发现什么?
2、当改变平行四边形的内角时,使其一个内角恰好为直角,此时得到一种特殊的平行四边形是什么图形?
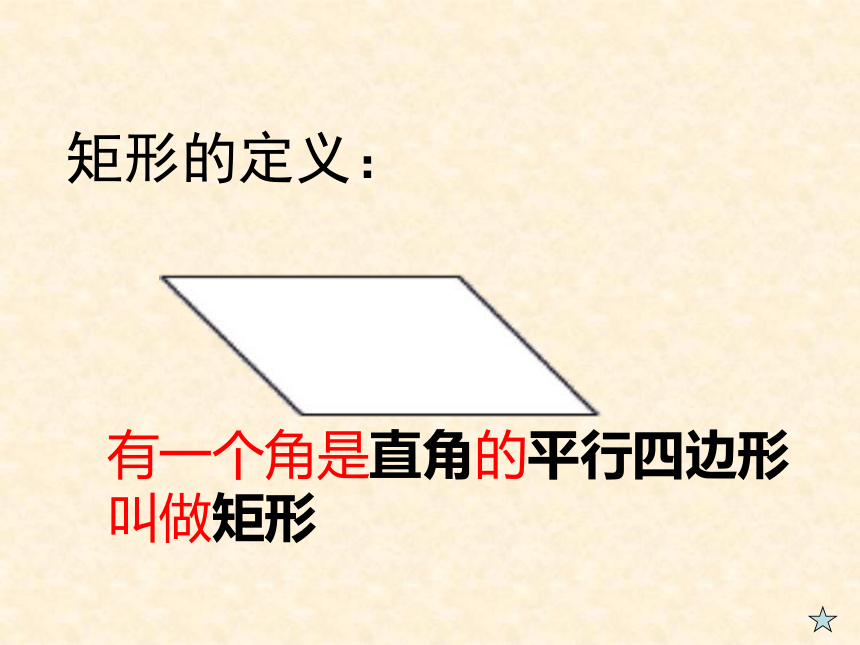
有一个角是直角的平行四边形叫做矩形
矩形的定义:
探究(二):矩形的性质
1、矩形具有平行四边形的性质吗? 2、在一个平行四边形活动框架上,用两根橡皮筋做出两条对角线,拉动一对不相邻的顶点,改变平行四边形的形状. ① 当∠α是直角时,平行四边形变成矩形,此时其它内角是什么样的角呢?
② 当∠α是锐角时,两条对角线的长度相等吗?
当∠α是钝角时,两条对角线的长度相等吗?
当∠α是直角时,平行四边形变为矩形,这时两 条对角线的长度具有怎样的关系?
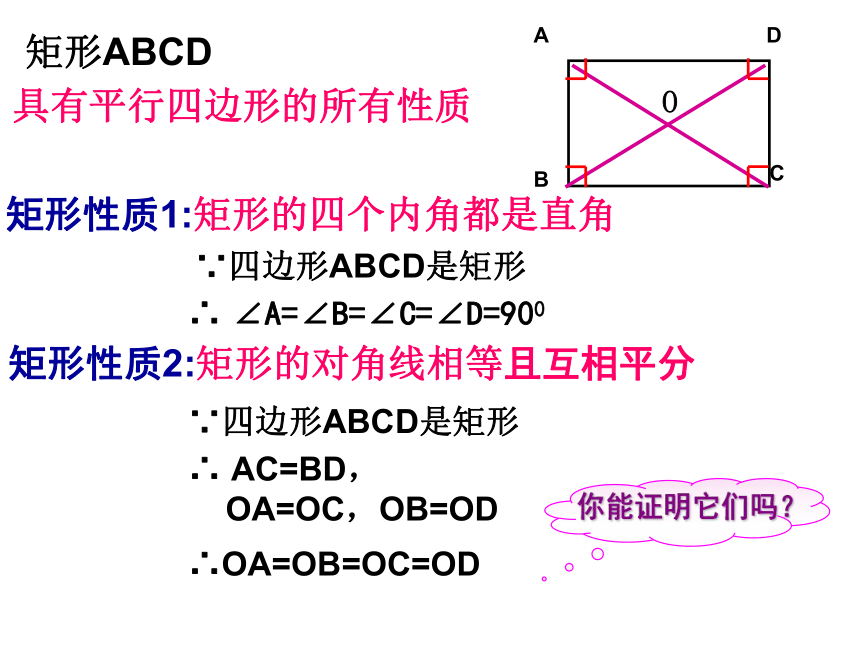
矩形性质1:矩形的四个内角都是直角
矩形性质2:矩形的对角线相等且互相平分
A
B
C
D
∵四边形ABCD是矩形
矩形ABCD
∴ AC=BD,
OA=OC,OB=OD
具有平行四边形的所有性质
O
∵四边形ABCD是矩形
∴ ∠A=∠B=∠C=∠D=900
∴OA=OB=OC=OD
你能证明它们吗?
矩形性质的运用:
例1:已知:如图,矩形ABCD的两条 对角线相交于点 O,∠AOB=60°,AB=4cm
求:矩形对角线的长.
A
B
C
D
O
解:
∵四边形ABCD是矩形.
∴AC与BD相等且互相平分.
∴OA=OB
又∵∠AOB=600
∴△OAB是等边三角形.
∴OA=AB=4(cm)
∴矩形的对角线长为AC=BD=8(cm)
O
A
B
C
D
探究(三):
直角三角形中斜边上的中线等于斜边的一半
D
A
B
C
O
在矩形ABCD中,AC、BD相交于点O,根据矩形的性质2,有AO=( )=( )=( )= ( )= ( ),因此可以得到直角三角形很重要的一个性质:
。
1.有一个角是直角的四边形是矩形( )
2.矩形的对角线相等且互相平分( )
1.矩形具有而平行四边形不具有的性质是( )
A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
2.下列性质中,矩形不一定具有的是( )
A 对边平行且相等 B 四个角都相等
C 对角线互相垂直 D 对角线相等
小结 反思
这节课你学到了什么
矩形的对边平行且相等;
矩形的对角相等且四个角都是直角;
矩形的对角线互相平分且相等;
矩形的性质:
直角三角形的性质:直角三角形斜边上的中线等于斜边的一半。
矩形的定义:
有一个角
是直角
收获与感悟:
我们的收获:
矩形之歌
脸蛋方方是矩形,例如黑板和门窗;
对角线段皆相等,相互交叉且平分;
内有直角三角形,斜边中线半斜边;
若要牢记其定义,直角平行四边形。
19.2.1 矩形(1)
托县第二中学 赵晓玉
学习目标:
1、探索矩形的定义和矩形的性质.
2、会初步运用矩形的定义和性质来 解决简单问题.
3、培养学生的观察能力、动手能力、自学能力、计算能力和逻辑思维能力.
探究(一):
1、用自制的平行四边形,轻轻的推动其中的一点,你会发现什么?
2、当改变平行四边形的内角时,使其一个内角恰好为直角,此时得到一种特殊的平行四边形是什么图形?
有一个角是直角的平行四边形叫做矩形
矩形的定义:
探究(二):矩形的性质
1、矩形具有平行四边形的性质吗? 2、在一个平行四边形活动框架上,用两根橡皮筋做出两条对角线,拉动一对不相邻的顶点,改变平行四边形的形状. ① 当∠α是直角时,平行四边形变成矩形,此时其它内角是什么样的角呢?
② 当∠α是锐角时,两条对角线的长度相等吗?
当∠α是钝角时,两条对角线的长度相等吗?
当∠α是直角时,平行四边形变为矩形,这时两 条对角线的长度具有怎样的关系?
矩形性质1:矩形的四个内角都是直角
矩形性质2:矩形的对角线相等且互相平分
A
B
C
D
∵四边形ABCD是矩形
矩形ABCD
∴ AC=BD,
OA=OC,OB=OD
具有平行四边形的所有性质
O
∵四边形ABCD是矩形
∴ ∠A=∠B=∠C=∠D=900
∴OA=OB=OC=OD
你能证明它们吗?
矩形性质的运用:
例1:已知:如图,矩形ABCD的两条 对角线相交于点 O,∠AOB=60°,AB=4cm
求:矩形对角线的长.
A
B
C
D
O
解:
∵四边形ABCD是矩形.
∴AC与BD相等且互相平分.
∴OA=OB
又∵∠AOB=600
∴△OAB是等边三角形.
∴OA=AB=4(cm)
∴矩形的对角线长为AC=BD=8(cm)
O
A
B
C
D
探究(三):
直角三角形中斜边上的中线等于斜边的一半
D
A
B
C
O
在矩形ABCD中,AC、BD相交于点O,根据矩形的性质2,有AO=( )=( )=( )= ( )= ( ),因此可以得到直角三角形很重要的一个性质:
。
1.有一个角是直角的四边形是矩形( )
2.矩形的对角线相等且互相平分( )
1.矩形具有而平行四边形不具有的性质是( )
A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
2.下列性质中,矩形不一定具有的是( )
A 对边平行且相等 B 四个角都相等
C 对角线互相垂直 D 对角线相等
小结 反思
这节课你学到了什么
矩形的对边平行且相等;
矩形的对角相等且四个角都是直角;
矩形的对角线互相平分且相等;
矩形的性质:
直角三角形的性质:直角三角形斜边上的中线等于斜边的一半。
矩形的定义:
有一个角
是直角
收获与感悟:
我们的收获:
矩形之歌
脸蛋方方是矩形,例如黑板和门窗;
对角线段皆相等,相互交叉且平分;
内有直角三角形,斜边中线半斜边;
若要牢记其定义,直角平行四边形。
