八年级数学12.3.1实数(1)
文档属性
| 名称 | 八年级数学12.3.1实数(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 610.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-06 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是光辉耀眼
老师的幸福是认识了你们
愿你们努力进取 永不言败
致亲爱的同学们
在古希腊,有一个很了不起的数学家,叫毕达哥拉斯,他开了一间学校,教了很多学生,毕达哥拉斯和他的学生们潜心研究数学,作出了好多的数学发现,比如“毕达哥拉斯定理”。这个定理,在我们中国叫“勾股定理”。毕达哥拉斯认为,世界上只存在着整数和分数,除此之外,就再也没有什么别的数了。可是,他有一个学生,叫希伯斯,却发现了一种既不是整数又不是分数的数,例如边长为1的正方形的对角线的长就是这种数。后来,人们就从希伯斯的发现中知道了原来除了整数和分数之外,世界上还存在着一种“新数”。
观察下列各数分别是什么数?
⑴3 ⑵ ⑶ ⑷ ⑸
整数
分数
有理数
有限小数或无限循环小数
(两个1之间依次多一个0)
1.1010010001…
=1.4142135623…
π=3.1415926535…
无限不循环小数
又叫做无理数
你认为对于无理数的理解应抓住几个要点呢?
游戏规则:同桌两人互相合作,一个同学任意说出三个数,另一个同学判断是有理数还是无理数。比一比,看哪个同学判断的最准确,看哪对同桌配合的最默契哟!
例如:
圆周率 及一些含有 的数都是无理数;
◆
◆像 这样根号去不掉的数也是无理数;
◆虽有一定的规律,但还是不循环的无限小数
也是无理数。
例如: 0.1010010001…〔两个1之间依次多1个0〕
-6.232232223…〔两个3之间依次多1个2 〕
无理数常见的三种类型
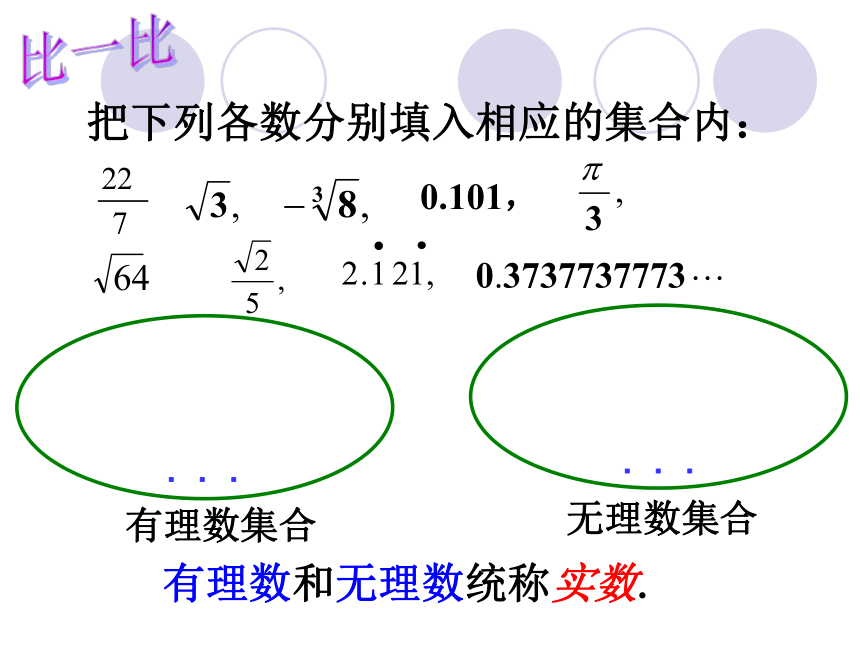
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
有理数和无理数统称实数.
◆ 你能仿照有理数的分类方式对实数
进行分类吗?
实数
有理数 有限小数或无限循环小数
无理数 无限不循环小数
实数的分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
探究
问题1.如图,直径为1个单位长度的圆从原点沿数轴 向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?
无理数可以用数轴上的点表示出来吗?
无理数 可以用数轴上的点来表示.
A
问题2.你能在数轴上表示出 和 - 吗?
1
1
1
1
把两个边长为1的小正方形通过剪、拼,得到一个大
正方形,大正方形的边长为 ,从而说明边长为1 的
小正方形的对角线为 。
探究
探究
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
★平面直角坐标系中的点和有序实数对是 一一对应的.
思考
-2的相反数是 ;-2的绝对值是
的相反数是 ; 的绝对值是
的相反数是 ; 的绝对值是
2
2
0的相反数是 ;0的绝对值是
0
0
观察以上求各数的相反数和绝对值的过程,你有什么发现?
有理数关于相反数和绝对值的意义
同样适合于实数
例1(1) 的相反数是 ,
-3.14的相反数是 ;
(2) 是 相反数,
是 的相反数;
(3) 的绝对值是 ;
(4)绝对值是 的数是 。
3.14-
4
①.一个实数不是有理数就是无理数。( )
②.一个实数不是正数就是负数。( )
2.下列说法正确的是( )
C、带根号的数都是无理数
×
A、无限小数都是无理数
B、无理数都是无限小数
D、不带根号的数都是有理数
B
1.判断正误
3.数轴上到原点的距离是 的点表示的数是 .
4、把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负实数集合:
1、两个概念:无理数、实数;
2、实数的两种分类方法;
3、两种一一对应关系;
4、有理数关于相反数和绝对值的意
义同样适合于实数。
通过本节课的学习,你觉得自己有哪些收获愿意和同学们一起分享呢?
作 业
一、必做题:P86 练习题 T2
习题T2
二、选做题:习题T3
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是光辉耀眼
老师的幸福是认识了你们
愿你们努力进取 永不言败
致亲爱的同学们
在古希腊,有一个很了不起的数学家,叫毕达哥拉斯,他开了一间学校,教了很多学生,毕达哥拉斯和他的学生们潜心研究数学,作出了好多的数学发现,比如“毕达哥拉斯定理”。这个定理,在我们中国叫“勾股定理”。毕达哥拉斯认为,世界上只存在着整数和分数,除此之外,就再也没有什么别的数了。可是,他有一个学生,叫希伯斯,却发现了一种既不是整数又不是分数的数,例如边长为1的正方形的对角线的长就是这种数。后来,人们就从希伯斯的发现中知道了原来除了整数和分数之外,世界上还存在着一种“新数”。
观察下列各数分别是什么数?
⑴3 ⑵ ⑶ ⑷ ⑸
整数
分数
有理数
有限小数或无限循环小数
(两个1之间依次多一个0)
1.1010010001…
=1.4142135623…
π=3.1415926535…
无限不循环小数
又叫做无理数
你认为对于无理数的理解应抓住几个要点呢?
游戏规则:同桌两人互相合作,一个同学任意说出三个数,另一个同学判断是有理数还是无理数。比一比,看哪个同学判断的最准确,看哪对同桌配合的最默契哟!
例如:
圆周率 及一些含有 的数都是无理数;
◆
◆像 这样根号去不掉的数也是无理数;
◆虽有一定的规律,但还是不循环的无限小数
也是无理数。
例如: 0.1010010001…〔两个1之间依次多1个0〕
-6.232232223…〔两个3之间依次多1个2 〕
无理数常见的三种类型
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
有理数和无理数统称实数.
◆ 你能仿照有理数的分类方式对实数
进行分类吗?
实数
有理数 有限小数或无限循环小数
无理数 无限不循环小数
实数的分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
探究
问题1.如图,直径为1个单位长度的圆从原点沿数轴 向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?
无理数可以用数轴上的点表示出来吗?
无理数 可以用数轴上的点来表示.
A
问题2.你能在数轴上表示出 和 - 吗?
1
1
1
1
把两个边长为1的小正方形通过剪、拼,得到一个大
正方形,大正方形的边长为 ,从而说明边长为1 的
小正方形的对角线为 。
探究
探究
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
★平面直角坐标系中的点和有序实数对是 一一对应的.
思考
-2的相反数是 ;-2的绝对值是
的相反数是 ; 的绝对值是
的相反数是 ; 的绝对值是
2
2
0的相反数是 ;0的绝对值是
0
0
观察以上求各数的相反数和绝对值的过程,你有什么发现?
有理数关于相反数和绝对值的意义
同样适合于实数
例1(1) 的相反数是 ,
-3.14的相反数是 ;
(2) 是 相反数,
是 的相反数;
(3) 的绝对值是 ;
(4)绝对值是 的数是 。
3.14-
4
①.一个实数不是有理数就是无理数。( )
②.一个实数不是正数就是负数。( )
2.下列说法正确的是( )
C、带根号的数都是无理数
×
A、无限小数都是无理数
B、无理数都是无限小数
D、不带根号的数都是有理数
B
1.判断正误
3.数轴上到原点的距离是 的点表示的数是 .
4、把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)负实数集合:
1、两个概念:无理数、实数;
2、实数的两种分类方法;
3、两种一一对应关系;
4、有理数关于相反数和绝对值的意
义同样适合于实数。
通过本节课的学习,你觉得自己有哪些收获愿意和同学们一起分享呢?
作 业
一、必做题:P86 练习题 T2
习题T2
二、选做题:习题T3
