河南省新乡市2020-2021学年八年级上学期期中考试数学试卷(word版含答案)
文档属性
| 名称 | 河南省新乡市2020-2021学年八年级上学期期中考试数学试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 416.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 16:05:29 | ||
图片预览

文档简介
2020-2021学年上学期期中考试八年级数学试题卷
总分:120分
考试时间:100分钟
一、选择题(每题3分,共30分)
1.下列图形中,不是轴对称图形的是 ( )
2.多边形的外角是 ( )
A.内角的对顶角
B.内角的邻角
C.与内角有公共顶点的角
D.内角的邻补角
3.
一个正多边形的一个内角是140°,则这个多边形是正多边形的边数为(
)
A.7
B.8
C.9
D.10
4.
已知点P1(a-1,3)和P2(2,b-1)关于x轴对称,则(a+b)2017的值为 ( )
A.0
B.-1
C.1
D.(-3)2017
5.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为 ( )
A.12
B.15
C.12或15
D.18
6.在平面直角坐标系中,
点A的坐标是(2,0),点B的坐标是(0,3),以AB腰画等腰三角形,则另一个顶点在坐标轴上的有(
).
A.3个
B.4个
C.5个
D.6个
7.在△ABC和△A′B′C′中,不能判断△ABC≌△A′B′C′的条件是 ( )
①AB=A′B′②BC=B′C′③AC=A′C′④∠A=∠A′⑤∠B=∠B′⑥∠C=C′
A.①②③
B.
①②⑤
C.①②④
D.②⑤⑥
8.如图,在△ABC中,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则△AMN的周长为(
)
A.6cm
B.5cm
C.4cm
D.3cm
9.如图,点A在DE上,AC=CE,∠1=∠2=∠3,则DE的长等于 ( )
A.DC
B.BC
C.AB
D.AE+AC
10.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,
则S△ABO∶S△BCO∶S△CAO等于 ( )
A.1∶1∶1
B.1∶2∶3
C.
3∶4∶5
D.
2∶3∶4
(第8题图)
(第9题图)
(第10题图)
二、填空题
(每题3分,共15分)
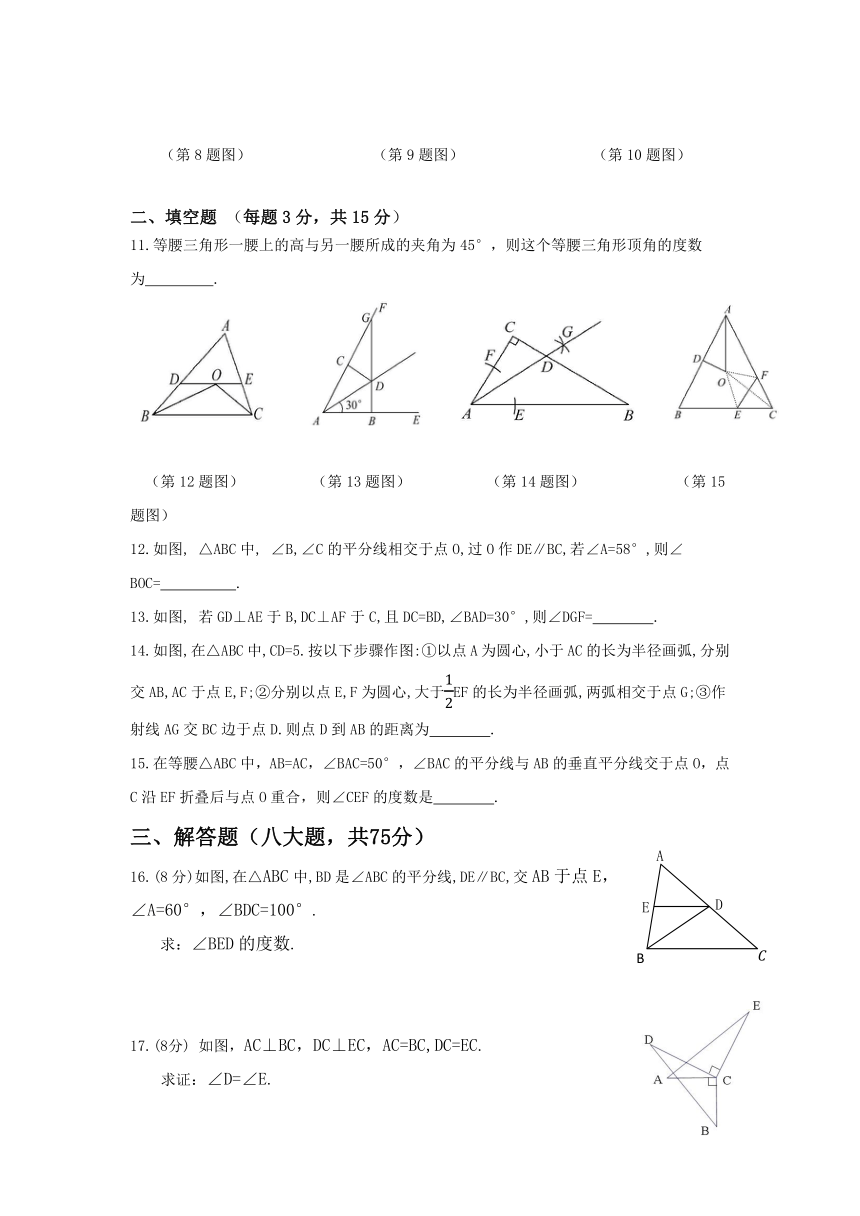
11.等腰三角形一腰上的高与另一腰所成的夹角为45°,则这个等腰三角形顶角的度数为
.
(第12题图)
(第13题图)
(第14题图)
(第15题图)
12.如图,
△ABC中,
∠B,∠C的平分线相交于点O,过O作DE∥BC,若∠A=58°,则∠BOC= .
13.如图,
若GD⊥AE于B,DC⊥AF于C,且DC=BD,∠BAD=30°,则∠DGF= .
14.如图,在△ABC中,CD=5.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则点D到AB的距离为 .
15.在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
三、解答题(八大题,共75分)
16.(8分)如图,在△ABC中,BD是∠ABC的平分线,DE∥BC,交AB于点E,
∠A=60°,∠BDC=100°.
求:∠BED的度数.
17.(8分)
如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC.
求证:∠D=∠E.
18.
(8分)如图,已知AC,BD相交于E点,∠A=∠B,
∠1=∠2.求证:AE=BE.
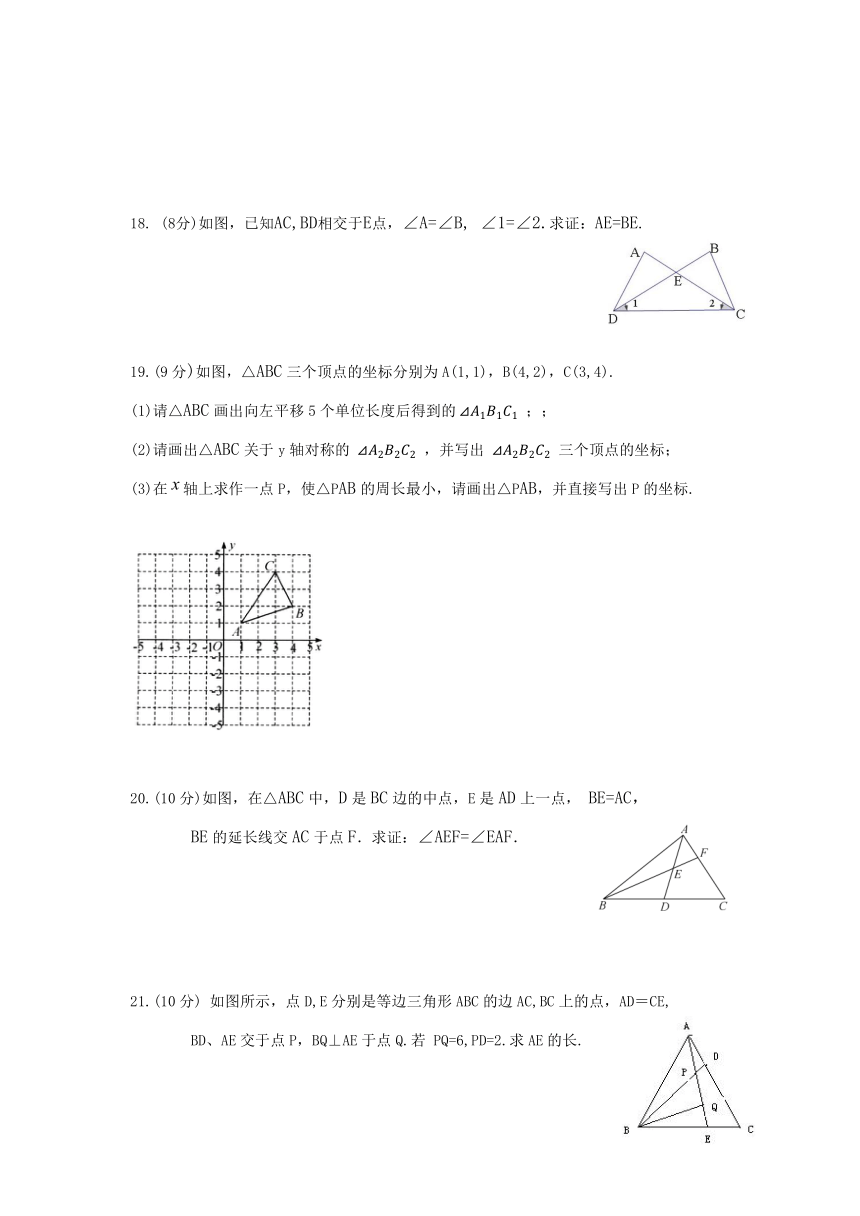
19.(9分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请△ABC画出向左平移5个单位长度后得到的
;;
(2)请画出△ABC关于y轴对称的
,并写出
三个顶点的坐标;
(3)在轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
20.(10分)如图,在△ABC中,D是BC边的中点,E是AD上一点,
BE=AC,
BE的延长线交AC于点F.求证:∠AEF=∠EAF.
21.(10分)
如图所示,点D,E分别是等边三角形ABC的边AC,BC上的点,AD=CE,
BD、AE交于点P,BQ⊥AE于点Q.若
PQ=6,PD=2.求AE的长.
22.
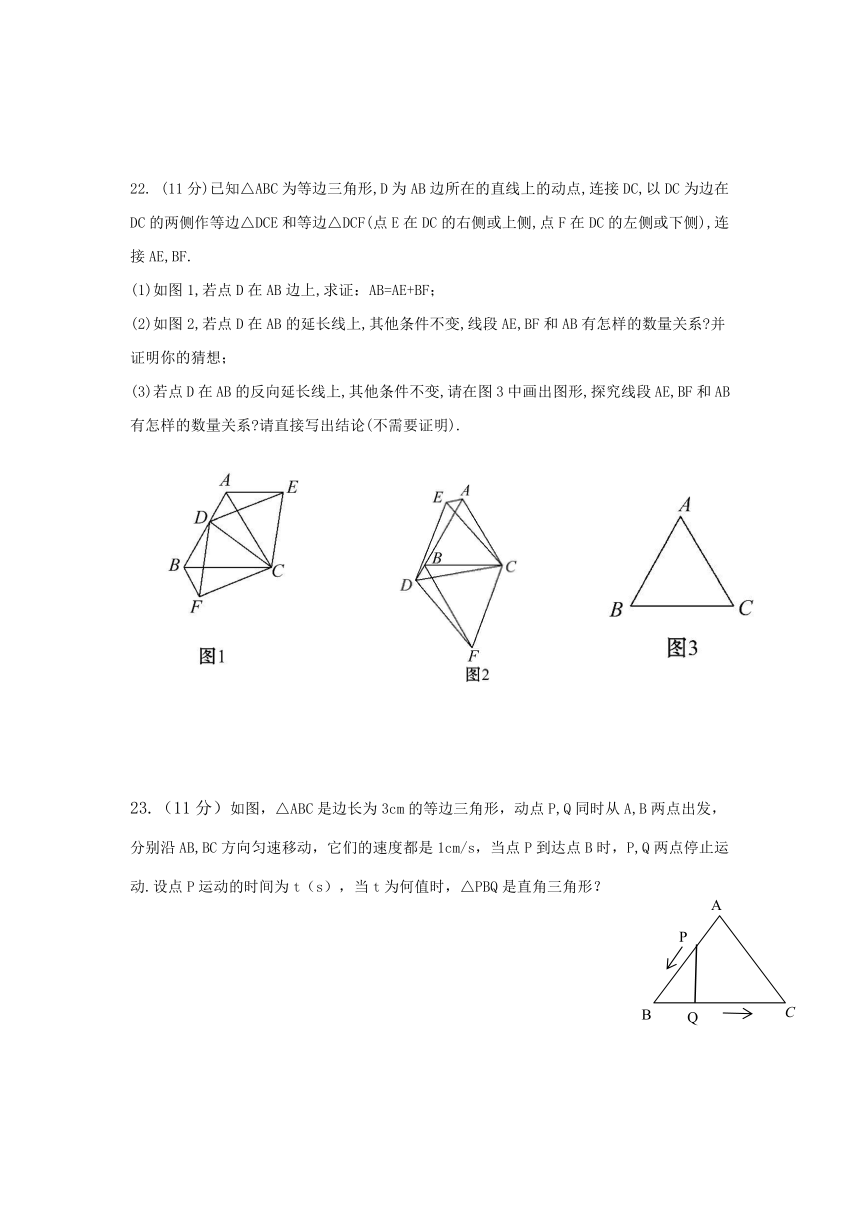
(11分)已知△ABC为等边三角形,D为AB边所在的直线上的动点,连接DC,以DC为边在DC的两侧作等边△DCE和等边△DCF(点E在DC的右侧或上侧,点F在DC的左侧或下侧),连接AE,BF.
(1)如图1,若点D在AB边上,求证:AB=AE+BF;
(2)如图2,若点D在AB的延长线上,其他条件不变,线段AE,BF和AB有怎样的数量关系?并证明你的猜想;
(3)若点D在AB的反向延长线上,其他条件不变,请在图3中画出图形,探究线段AE,BF和AB有怎样的数量关系?请直接写出结论(不需要证明).
23.(11分)如图,△ABC是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点停止运动.设点P运动的时间为t(s),当t为何值时,△PBQ是直角三角形?
2020-2021学年上学期八年级数学期中测试卷答案
一、选择
1.A
2.D
3.C
4.C
5.B
6.D
7.C
8.A
9.C
10.D
二、填空
11.45?或135?
12.
119?
13.
150?
14.
5
15.
50?
三、解答题
16.解:∵∠ABD+∠A=∠BDC=100°
∠A=60°
∴∠ABD=40°----------------------2分
∵
BD平分∠ABC
∴∠DBC=∠ABD=40°---------------4分
∵ED∥BC
∴∠EDB=∠DBC=40°---------------6分
在△BED中
∴∠BED=180°-∠ABD-∠EDB=100°---8分
17.解析:△BCD≌△ACE(SAS)
---------7分
∠D=∠E
----------------------8分
18.(证法不唯一)解析:∵∠1=∠2
∴DE=CE
----------------------------2分
∵∠A=∠B,∠AED=∠BEC
∴△ADE≌△BCE(AAS)
----------7分
∴AE=BE
---------8分
(1)图略
------------------------2分
(2)图略,
(-1,1)
(-4,2)
(-3,4)--7分
(3)图略,P(2,0)
-----------------------9分
20.解析:过B作BM∥AC交AD延长线于点M
或延长AD至点M,使DN=AD,连接BM
----1分
证△BDM≌△CDA
----------------------5分
∴∠M=∠CAD
BM=AC
----------------------6分
∵BE=AC
∴BM=BE
---------------------7分
∴∠M=∠BED
-------------------8分
∴∠CAD=∠BED
---------------9分
∵∠BED=∠AEF
∴∠FAE=∠AEF
--------------10分
21.解析:△ABD≌△CAE(SAS)
------4分
∴BD=AE
∠ABD=∠CAE
---------5分
∵∠BPQ=∠ABD+∠BAE
∴∠BPQ=∠CAE+∠BAE=∠BAC=60°
-----6分
∵BQ⊥AE
∴∠BQO=90°
∴在Rt△BPQ中,∠BPQ=30°------7分
∴BP=2PQ=2×6=12
-----8分
∴BD=BP+PD=14
--------9分
∴AE=BD=14
----10分
22.解析:(1)△ADC≌△BFC(SAS)
∴AD=BF
△BDC≌△AEC(SAS)
∴BD=AE
∵AB=AD+BD
∴AB=BF+AE
-----4分
(2)AB=BF-AE
-----5分
理由:△ADC≌△BFC(SAS)
∴AD=BF
△BDC≌△AEC(SAS)
∴BD=AE
∵AB=AD-BD
∴AB=BF-AE
----9分
(3)AB=AE-BF
---11分
23.解析:依题得
AP=t,PB=3-t,BQ=t
∵△ABC为等边三角形
∴∠B=60°
-------------2分
①若∠BQP=90°时,∠BPQ=30°
在Rt△BQP中,PB=2BQ
即
3-t=2t
解得
t=1
----------6分
②若∠BPQ=90°时,∠BQP=30°
在Rt△BPQ中,BQ=2BP
即
2(3-t)=t
解得
t=2
--------10分
综上所述:当t=1或2时,△BPQ为直角三角形
-----11分
总分:120分
考试时间:100分钟
一、选择题(每题3分,共30分)
1.下列图形中,不是轴对称图形的是 ( )
2.多边形的外角是 ( )
A.内角的对顶角
B.内角的邻角
C.与内角有公共顶点的角
D.内角的邻补角
3.
一个正多边形的一个内角是140°,则这个多边形是正多边形的边数为(
)
A.7
B.8
C.9
D.10
4.
已知点P1(a-1,3)和P2(2,b-1)关于x轴对称,则(a+b)2017的值为 ( )
A.0
B.-1
C.1
D.(-3)2017
5.等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为 ( )
A.12
B.15
C.12或15
D.18
6.在平面直角坐标系中,
点A的坐标是(2,0),点B的坐标是(0,3),以AB腰画等腰三角形,则另一个顶点在坐标轴上的有(
).
A.3个
B.4个
C.5个
D.6个
7.在△ABC和△A′B′C′中,不能判断△ABC≌△A′B′C′的条件是 ( )
①AB=A′B′②BC=B′C′③AC=A′C′④∠A=∠A′⑤∠B=∠B′⑥∠C=C′
A.①②③
B.
①②⑤
C.①②④
D.②⑤⑥
8.如图,在△ABC中,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则△AMN的周长为(
)
A.6cm
B.5cm
C.4cm
D.3cm
9.如图,点A在DE上,AC=CE,∠1=∠2=∠3,则DE的长等于 ( )
A.DC
B.BC
C.AB
D.AE+AC
10.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,
则S△ABO∶S△BCO∶S△CAO等于 ( )
A.1∶1∶1
B.1∶2∶3
C.
3∶4∶5
D.
2∶3∶4
(第8题图)
(第9题图)
(第10题图)
二、填空题
(每题3分,共15分)
11.等腰三角形一腰上的高与另一腰所成的夹角为45°,则这个等腰三角形顶角的度数为
.
(第12题图)
(第13题图)
(第14题图)
(第15题图)
12.如图,
△ABC中,
∠B,∠C的平分线相交于点O,过O作DE∥BC,若∠A=58°,则∠BOC= .
13.如图,
若GD⊥AE于B,DC⊥AF于C,且DC=BD,∠BAD=30°,则∠DGF= .
14.如图,在△ABC中,CD=5.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则点D到AB的距离为 .
15.在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
三、解答题(八大题,共75分)
16.(8分)如图,在△ABC中,BD是∠ABC的平分线,DE∥BC,交AB于点E,
∠A=60°,∠BDC=100°.
求:∠BED的度数.
17.(8分)
如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC.
求证:∠D=∠E.
18.
(8分)如图,已知AC,BD相交于E点,∠A=∠B,
∠1=∠2.求证:AE=BE.
19.(9分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请△ABC画出向左平移5个单位长度后得到的
;;
(2)请画出△ABC关于y轴对称的
,并写出
三个顶点的坐标;
(3)在轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
20.(10分)如图,在△ABC中,D是BC边的中点,E是AD上一点,
BE=AC,
BE的延长线交AC于点F.求证:∠AEF=∠EAF.
21.(10分)
如图所示,点D,E分别是等边三角形ABC的边AC,BC上的点,AD=CE,
BD、AE交于点P,BQ⊥AE于点Q.若
PQ=6,PD=2.求AE的长.
22.
(11分)已知△ABC为等边三角形,D为AB边所在的直线上的动点,连接DC,以DC为边在DC的两侧作等边△DCE和等边△DCF(点E在DC的右侧或上侧,点F在DC的左侧或下侧),连接AE,BF.
(1)如图1,若点D在AB边上,求证:AB=AE+BF;
(2)如图2,若点D在AB的延长线上,其他条件不变,线段AE,BF和AB有怎样的数量关系?并证明你的猜想;
(3)若点D在AB的反向延长线上,其他条件不变,请在图3中画出图形,探究线段AE,BF和AB有怎样的数量关系?请直接写出结论(不需要证明).
23.(11分)如图,△ABC是边长为3cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点停止运动.设点P运动的时间为t(s),当t为何值时,△PBQ是直角三角形?
2020-2021学年上学期八年级数学期中测试卷答案
一、选择
1.A
2.D
3.C
4.C
5.B
6.D
7.C
8.A
9.C
10.D
二、填空
11.45?或135?
12.
119?
13.
150?
14.
5
15.
50?
三、解答题
16.解:∵∠ABD+∠A=∠BDC=100°
∠A=60°
∴∠ABD=40°----------------------2分
∵
BD平分∠ABC
∴∠DBC=∠ABD=40°---------------4分
∵ED∥BC
∴∠EDB=∠DBC=40°---------------6分
在△BED中
∴∠BED=180°-∠ABD-∠EDB=100°---8分
17.解析:△BCD≌△ACE(SAS)
---------7分
∠D=∠E
----------------------8分
18.(证法不唯一)解析:∵∠1=∠2
∴DE=CE
----------------------------2分
∵∠A=∠B,∠AED=∠BEC
∴△ADE≌△BCE(AAS)
----------7分
∴AE=BE
---------8分
(1)图略
------------------------2分
(2)图略,
(-1,1)
(-4,2)
(-3,4)--7分
(3)图略,P(2,0)
-----------------------9分
20.解析:过B作BM∥AC交AD延长线于点M
或延长AD至点M,使DN=AD,连接BM
----1分
证△BDM≌△CDA
----------------------5分
∴∠M=∠CAD
BM=AC
----------------------6分
∵BE=AC
∴BM=BE
---------------------7分
∴∠M=∠BED
-------------------8分
∴∠CAD=∠BED
---------------9分
∵∠BED=∠AEF
∴∠FAE=∠AEF
--------------10分
21.解析:△ABD≌△CAE(SAS)
------4分
∴BD=AE
∠ABD=∠CAE
---------5分
∵∠BPQ=∠ABD+∠BAE
∴∠BPQ=∠CAE+∠BAE=∠BAC=60°
-----6分
∵BQ⊥AE
∴∠BQO=90°
∴在Rt△BPQ中,∠BPQ=30°------7分
∴BP=2PQ=2×6=12
-----8分
∴BD=BP+PD=14
--------9分
∴AE=BD=14
----10分
22.解析:(1)△ADC≌△BFC(SAS)
∴AD=BF
△BDC≌△AEC(SAS)
∴BD=AE
∵AB=AD+BD
∴AB=BF+AE
-----4分
(2)AB=BF-AE
-----5分
理由:△ADC≌△BFC(SAS)
∴AD=BF
△BDC≌△AEC(SAS)
∴BD=AE
∵AB=AD-BD
∴AB=BF-AE
----9分
(3)AB=AE-BF
---11分
23.解析:依题得
AP=t,PB=3-t,BQ=t
∵△ABC为等边三角形
∴∠B=60°
-------------2分
①若∠BQP=90°时,∠BPQ=30°
在Rt△BQP中,PB=2BQ
即
3-t=2t
解得
t=1
----------6分
②若∠BPQ=90°时,∠BQP=30°
在Rt△BPQ中,BQ=2BP
即
2(3-t)=t
解得
t=2
--------10分
综上所述:当t=1或2时,△BPQ为直角三角形
-----11分
同课章节目录
