4.2.1 图形的旋转同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
2 图形的旋转
第1课时
考点突破
考点1 旋转的概念
例1 如图,△ABC为等边三角形,点P在△ABC中,将△ABP旋转后能与△CBP'重合.
(1)旋转中心是哪一点?
(2)旋转角是多少度?
(3)△BPP'是什么三角形?
思路导引: 确定一个图形经过旋转得到另一个图形的旋转中心,关键看对应点是否都旋转了相同的角度,或者对应点到旋转中心的距离是否相等来判断.
方法归纳
1.我们可以从旋转过程中的不动点,或根据对应点到旋转中心的距离相等,或对应点所连线段的垂直平分线的交点等方面来确定旋转中心。
2.找旋转角时,一般先找出对应点,然后连接对应点和旋转中心,其夹角即为旋转角.
题组训练
1.下列运动属于旋转的是( )
A.滚动过程中的篮球的滚动 B.风筝在空中飘动
C.钟表的钟摆的摆动 D.一个图形沿某直线对折的过程
2.将左图按顺时针方向旋转90°后得到的是( )
3.观察下列四组图形,其中与另外三组不同的是( )
4.如图所示,如果把钟表的指针看成四边形AOBC,它绕着点O旋转到四边形DOEF位置,在这个旋转过程中:旋转中心是_________,旋转角是_________,经过旋转点A转到点________,线段OB的对应线段是_________,∠C与__________是对应角.
考点2 旋转的性质
例2 如图,点E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE'的位置,若AE=1 cm,BE= 2 cm,CE = 3 cm,求∠BE'C的度数.
思路导引: 连接EE',由旋转的性质可得CE'和BE'的长由勾股定理的逆定理可得△ECE是直角三角形进而可求出∠BE'C的度数.
方法归纳
旋转性质的基本应用:
1.证明线段或角相等
(1)根据旋转角相等,对应点与旋转中心的连线相等可得线段或角相等;
(2)根据旋转前、后的图形全等,可得图形的对应线段、对应角相等
(2.计算图形的面积、线段的长度或角的大小.
题组训练
5.如图,△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°得到△A'OB',边A'B'与边OB交于点C(A'不在OB上),则∠A'CO的度数为( )
A. 22? B. 82° C. 60° D.52°
第5题图 第6题图
6.(庆阳)如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB′,若∠AOB=21°,则∠AOB'的度数是( )
A. 21° B. 45° C. 42° D. 24°
7.(怀化)旋转不改变图形的___________和___________.
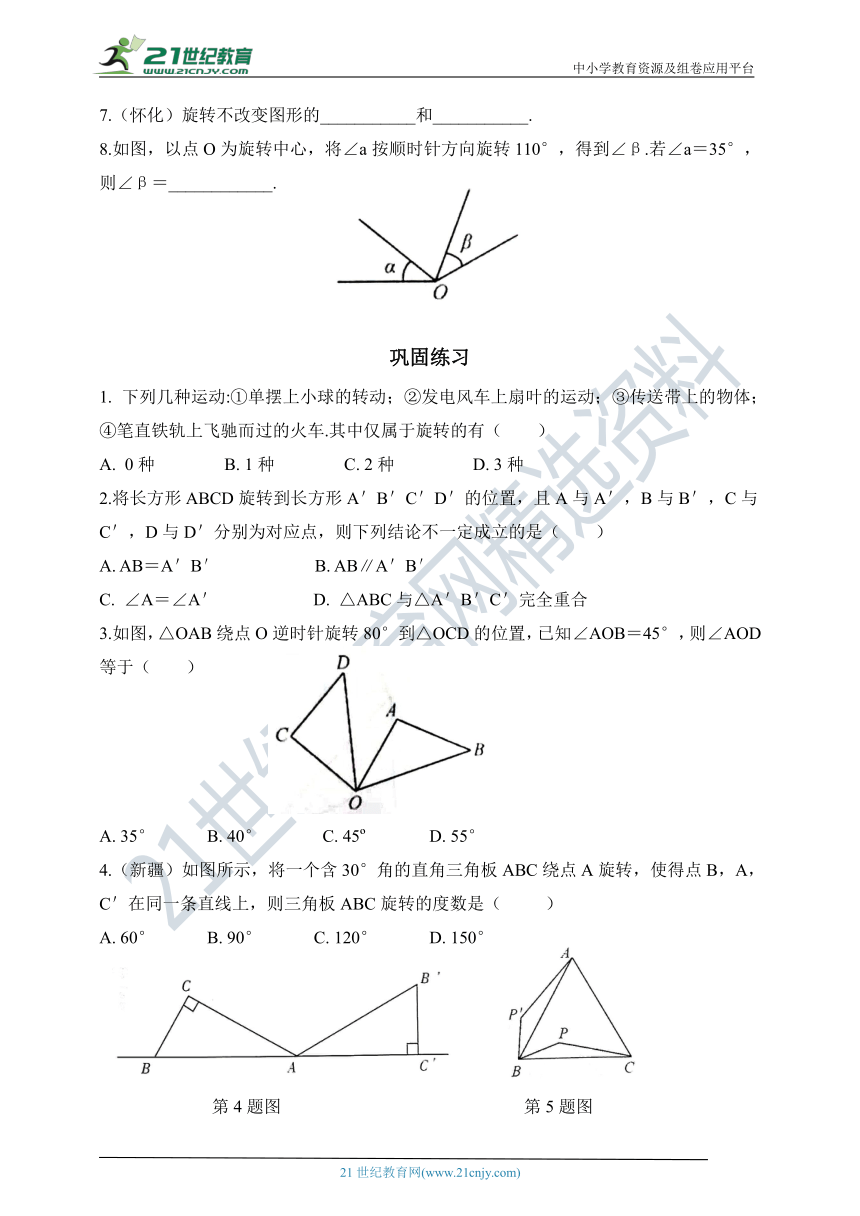
8.如图,以点O为旋转中心,将∠a按顺时针方向旋转110°,得到∠β.若∠a=35°,则∠β=____________.
巩固练习
下列几种运动:①单摆上小球的转动;②发电风车上扇叶的运动;③传送带上的物体;④笔直铁轨上飞驰而过的火车.其中仅属于旋转的有( )
0种 B. 1种 C. 2种 D. 3种
2.将长方形ABCD旋转到长方形A'B'C'D'的位置,且A与A',B与B',C与C',D与D'分别为对应点,则下列结论不一定成立的是( )
A. AB=A'B′ B. AB∥A'B′
C. ∠A=∠A' D. △ABC与△A'B'C'完全重合
3.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
A. 35° B. 40° C. 45? D. 55°
4.(新疆)如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C'在同一条直线上,则三角板ABC旋转的度数是( )
A. 60° B. 90° C. 120° D. 150°
第4题图 第5题图
5.如图所示,P是正△ABC内的一点,若将△PBC绕点B逆时针旋转到△P'BA的位置,则点C的对应点是_________;∠PBC的对应角是_________;边PC的对应线段是________;∠PBP'的度数是__________。
6.如图,∠MPN=48°,如果线段AB关于PM对称的线段是A′B′,关于PN对称的线段是A"B",那么线段A"B"可以看成由A′B′绕点P按________方向旋转_________°得到的.
第6题图 第7题图
7.(镇江)如图,将△OAB绕着点O逆时针旋转两次得到△OA"B",每次旋转的角度都是50°,若∠B"OA=120°,则∠AOB=__________.
8.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA′,若∠1=20°,则∠B的度数是( )
70° B. 65° C. 60° D. 55°
9.如图,已知P是正方形ABCD内的一点,以点B为旋转中心,把△PBC沿逆时针方向旋转90°,得到△P'BA,连接P'P,若PB=3cm,则 P'P=_________,∠P'PB=____________.
第9题图 第10题图
10.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°到OA′,则点A'的坐标是___________。
11.(荆州)如图①,正方形ABCD的边AB,AD分别在等腰直角△AEF的腰AE,AF上,点C在△AEF内,则有DF=BE(不必证明).将正方形ABCD绕点A逆时针旋转一定角度a(0°<a<90°)后,连接BE,DF.请在图②中用实线补全图形,这时DF=BE还成立吗?请说明理由.
参考答案
考点突破
例1 解:(1)旋转中心是点B.
(2)∠ABC与∠PBP′是旋转角
(3)由旋转知BP=BP',又∵△ABC为等边三角形∴∠ABC=60°∴BPP'是等边三角形。
题组训练
C 2. A 3. C
4.点O ∠AOD(或∠BOE) D E ∠F
例2 解:连接EE',由旋转的性质可知, CE'=AE=1 cm, BE'=BE=2 cm,
∠EBE'=∠ABC=90°,∴∠BE'E=45°且由勾股定理,得EE'=.又∵12+(2)2=32,即EC'2+E'E2=CE2,∴△ECE'是直角三角形,∠EE'C=90°∴∠BE'C=∠BE'E+∠EE'C=45°+90°=135°.
题组训练
B 6. D 7. 形状 大小 8. 35?
巩固练习
C 2. B 3. A 4. D 5. A
逆时针 96 7. 20
8. B 9. 3 10. (-4,3)
11.解:补全图形如图所示,DF=BE还成立,理由是:在正方形ABCD和等腰直角△AEF中,AD=AB,AF=AE,∠FAE=∠DAB=90°。
∴∠FAD=∠EAB.∴△ADF≌△ABE(SAS)∴DF=BE。
_21?????????è?????(www.21cnjy.com)_
第四章 图形的平移与旋转
2 图形的旋转
第1课时
考点突破
考点1 旋转的概念
例1 如图,△ABC为等边三角形,点P在△ABC中,将△ABP旋转后能与△CBP'重合.
(1)旋转中心是哪一点?
(2)旋转角是多少度?
(3)△BPP'是什么三角形?
思路导引: 确定一个图形经过旋转得到另一个图形的旋转中心,关键看对应点是否都旋转了相同的角度,或者对应点到旋转中心的距离是否相等来判断.
方法归纳
1.我们可以从旋转过程中的不动点,或根据对应点到旋转中心的距离相等,或对应点所连线段的垂直平分线的交点等方面来确定旋转中心。
2.找旋转角时,一般先找出对应点,然后连接对应点和旋转中心,其夹角即为旋转角.
题组训练
1.下列运动属于旋转的是( )
A.滚动过程中的篮球的滚动 B.风筝在空中飘动
C.钟表的钟摆的摆动 D.一个图形沿某直线对折的过程
2.将左图按顺时针方向旋转90°后得到的是( )
3.观察下列四组图形,其中与另外三组不同的是( )
4.如图所示,如果把钟表的指针看成四边形AOBC,它绕着点O旋转到四边形DOEF位置,在这个旋转过程中:旋转中心是_________,旋转角是_________,经过旋转点A转到点________,线段OB的对应线段是_________,∠C与__________是对应角.
考点2 旋转的性质
例2 如图,点E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE'的位置,若AE=1 cm,BE= 2 cm,CE = 3 cm,求∠BE'C的度数.
思路导引: 连接EE',由旋转的性质可得CE'和BE'的长由勾股定理的逆定理可得△ECE是直角三角形进而可求出∠BE'C的度数.
方法归纳
旋转性质的基本应用:
1.证明线段或角相等
(1)根据旋转角相等,对应点与旋转中心的连线相等可得线段或角相等;
(2)根据旋转前、后的图形全等,可得图形的对应线段、对应角相等
(2.计算图形的面积、线段的长度或角的大小.
题组训练
5.如图,△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°得到△A'OB',边A'B'与边OB交于点C(A'不在OB上),则∠A'CO的度数为( )
A. 22? B. 82° C. 60° D.52°
第5题图 第6题图
6.(庆阳)如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB′,若∠AOB=21°,则∠AOB'的度数是( )
A. 21° B. 45° C. 42° D. 24°
7.(怀化)旋转不改变图形的___________和___________.
8.如图,以点O为旋转中心,将∠a按顺时针方向旋转110°,得到∠β.若∠a=35°,则∠β=____________.
巩固练习
下列几种运动:①单摆上小球的转动;②发电风车上扇叶的运动;③传送带上的物体;④笔直铁轨上飞驰而过的火车.其中仅属于旋转的有( )
0种 B. 1种 C. 2种 D. 3种
2.将长方形ABCD旋转到长方形A'B'C'D'的位置,且A与A',B与B',C与C',D与D'分别为对应点,则下列结论不一定成立的是( )
A. AB=A'B′ B. AB∥A'B′
C. ∠A=∠A' D. △ABC与△A'B'C'完全重合
3.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
A. 35° B. 40° C. 45? D. 55°
4.(新疆)如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C'在同一条直线上,则三角板ABC旋转的度数是( )
A. 60° B. 90° C. 120° D. 150°
第4题图 第5题图
5.如图所示,P是正△ABC内的一点,若将△PBC绕点B逆时针旋转到△P'BA的位置,则点C的对应点是_________;∠PBC的对应角是_________;边PC的对应线段是________;∠PBP'的度数是__________。
6.如图,∠MPN=48°,如果线段AB关于PM对称的线段是A′B′,关于PN对称的线段是A"B",那么线段A"B"可以看成由A′B′绕点P按________方向旋转_________°得到的.
第6题图 第7题图
7.(镇江)如图,将△OAB绕着点O逆时针旋转两次得到△OA"B",每次旋转的角度都是50°,若∠B"OA=120°,则∠AOB=__________.
8.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA′,若∠1=20°,则∠B的度数是( )
70° B. 65° C. 60° D. 55°
9.如图,已知P是正方形ABCD内的一点,以点B为旋转中心,把△PBC沿逆时针方向旋转90°,得到△P'BA,连接P'P,若PB=3cm,则 P'P=_________,∠P'PB=____________.
第9题图 第10题图
10.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°到OA′,则点A'的坐标是___________。
11.(荆州)如图①,正方形ABCD的边AB,AD分别在等腰直角△AEF的腰AE,AF上,点C在△AEF内,则有DF=BE(不必证明).将正方形ABCD绕点A逆时针旋转一定角度a(0°<a<90°)后,连接BE,DF.请在图②中用实线补全图形,这时DF=BE还成立吗?请说明理由.
参考答案
考点突破
例1 解:(1)旋转中心是点B.
(2)∠ABC与∠PBP′是旋转角
(3)由旋转知BP=BP',又∵△ABC为等边三角形∴∠ABC=60°∴BPP'是等边三角形。
题组训练
C 2. A 3. C
4.点O ∠AOD(或∠BOE) D E ∠F
例2 解:连接EE',由旋转的性质可知, CE'=AE=1 cm, BE'=BE=2 cm,
∠EBE'=∠ABC=90°,∴∠BE'E=45°且由勾股定理,得EE'=.又∵12+(2)2=32,即EC'2+E'E2=CE2,∴△ECE'是直角三角形,∠EE'C=90°∴∠BE'C=∠BE'E+∠EE'C=45°+90°=135°.
题组训练
B 6. D 7. 形状 大小 8. 35?
巩固练习
C 2. B 3. A 4. D 5. A
逆时针 96 7. 20
8. B 9. 3 10. (-4,3)
11.解:补全图形如图所示,DF=BE还成立,理由是:在正方形ABCD和等腰直角△AEF中,AD=AB,AF=AE,∠FAE=∠DAB=90°。
∴∠FAD=∠EAB.∴△ADF≌△ABE(SAS)∴DF=BE。
_21?????????è?????(www.21cnjy.com)_
