人教版数学九年级上册25 概率初步 单元练习(Word版 附答案)
文档属性
| 名称 | 人教版数学九年级上册25 概率初步 单元练习(Word版 附答案) | 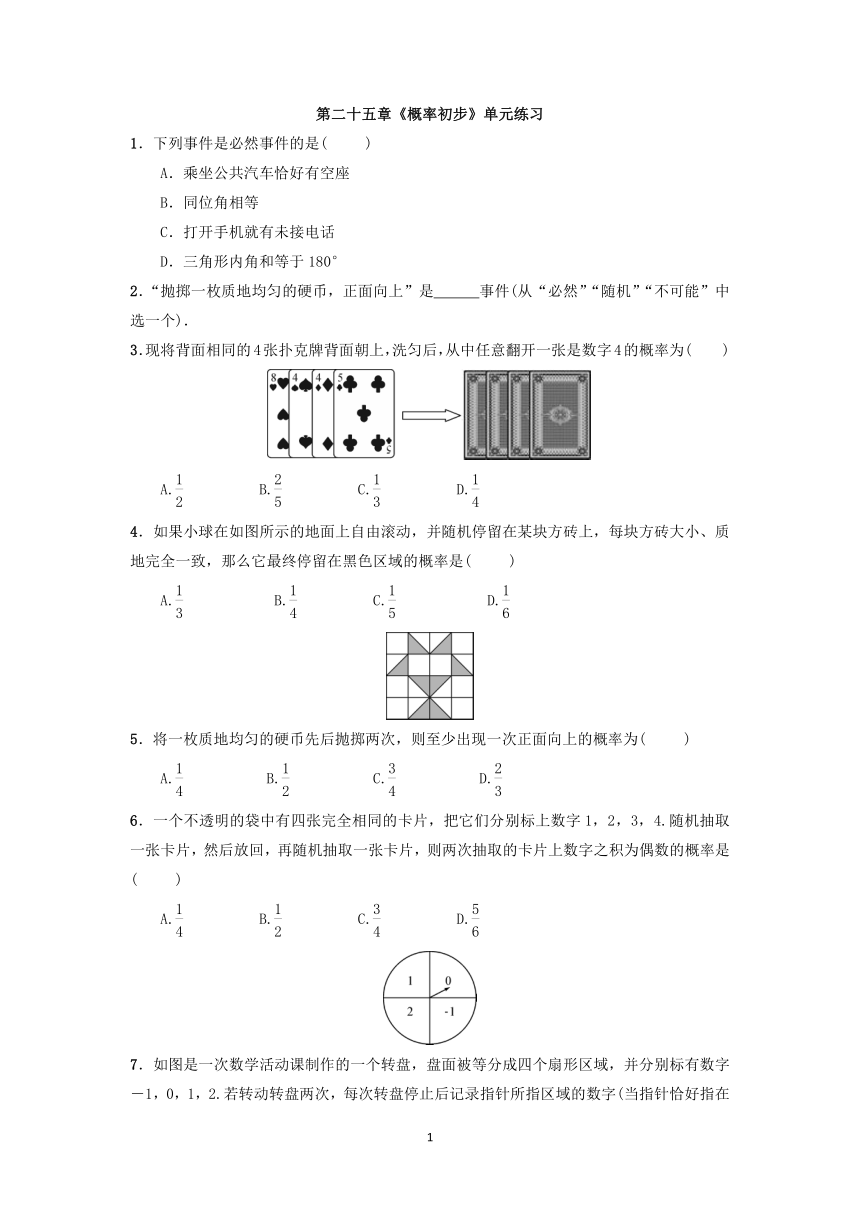 | |
| 格式 | docx | ||
| 文件大小 | 330.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 12:43:15 | ||
图片预览



文档简介
第二十五章《概率初步》单元练习
1.下列事件是必然事件的是( )
A.乘坐公共汽车恰好有空座
B.同位角相等
C.打开手机就有未接电话
D.三角形内角和等于180°
2.“抛掷一枚质地均匀的硬币,正面向上”是 事件(从“必然”“随机”“不可能”中选一个).
3.现将背面相同的4张扑克牌背面朝上,洗匀后,从中任意翻开一张是数字4的概率为( )
A. B. C. D.
4.如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
A. B. C. D.
5.将一枚质地均匀的硬币先后抛掷两次,则至少出现一次正面向上的概率为( )
A. B. C. D.
6.一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1,2,3,4.随机抽取一张卡片,然后放回,再随机抽取一张卡片,则两次抽取的卡片上数字之积为偶数的概率是( )
A. B. C. D.
7.如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
A. B. C. D.
8.甲、乙两位同学各抛掷一枚质地均匀的骰子,他们抛掷的点数分别记为a,b,则a+b=9的概率为 .
9.有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3 cm,7 cm,9 cm;乙盒子中装有4张卡片,卡片上分别写着2 cm,4 cm,6 cm,8 cm;盒子外有一张写着5 cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
10.袋子中有红球、白球共10个,这些球除颜色外都相同,将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断重复这一过程,摸了100次后,发现有30次摸到红球,请你估计这个袋中红球约有 个.
11.现有4张卡片,其中3张卡片正面上的图案是“”,1张卡片正面上的图案是“”,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取2张,则这2张卡片正面图案相同的概率是( )
A. B. C. D.
12.毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小明将这五位名人介绍分别写在五张完全相同的知识卡片上,小亮从中随机抽取一张,卡片上介绍的人物是汉朝以后出生的概率是 .
13.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m-n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
14.“服务他人,提升自我”,来自九年级的5名同学(3男2女)成立了“交通秩序维护”小分队.若从该小分队中任选两名同学进行交通秩序维护,则恰好是一男一女的概率是 .
15.为进一步深化基础教育课程改革,构建符合素质教育要求的学校课程体系,某学校自主开发了A:书法,B:阅读,C:足球,D:器乐四门校本选修课程供学生选择,每门课程被选到的机会均等.
(1)学生小红计划选修两门课程,求她恰好选修书法和器乐的概率;
(2)若学生小明和小刚各计划选修一门课程,则他们两人恰好选修同一门课程的概率为多少?
16.主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重;
B.放下利益,彼此平衡;
C.放下性格,彼此成就;
D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如下两幅不完整的图表.
观点
频数
频率
A
a
0.2
B
12
0.24
C
8
b
D
20
0.4
354330584200
请根据图表中提供的信息,解答下列问题:
(1)参加本次讨论的学生共有 人;
(2)表中a= ,b= ;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.
参考答案:
1.D
2. 随机 .
3.A
4.B
5.C
6.C
7.C
8. .
9.解:(1)画树状图:
共有12种等可能的结果,其中能组成三角形的有7种,
∴P(能组成三角形)=.
(2)∵能与5 cm组成直角三角形的有1种,
∴P(能组成直角三角形)=.
10.3.
11.D
12. .
13.B
14. .
15.解:(1)列表如下:
A
B
C
D
A
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,D)
D
(D,A)
(D,B)
(D,C)
由表格可知,共有12种等可能的结果,其中小红选修书法和器乐的结果有2种,
∴P(小红选修书法和器乐)==.
(2)画树状图如下:
由树状图可知共有16种等可能的结果,其中小明和小刚恰好选修同一门课程的结果有4种,
∴P(小明和小刚恰好选修同一门课程)==.
16.(1)50;
(2)a=10,b=0.16;
解:(3)如图.
(4)画树状图如下:
由树状图可知,共有12种等可能情况,选中观点D(合理竞争,合作双赢)的情况有6种,
∴选中观点D(合理竞争,合作双赢)的概率为=.
1.下列事件是必然事件的是( )
A.乘坐公共汽车恰好有空座
B.同位角相等
C.打开手机就有未接电话
D.三角形内角和等于180°
2.“抛掷一枚质地均匀的硬币,正面向上”是 事件(从“必然”“随机”“不可能”中选一个).
3.现将背面相同的4张扑克牌背面朝上,洗匀后,从中任意翻开一张是数字4的概率为( )
A. B. C. D.
4.如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
A. B. C. D.
5.将一枚质地均匀的硬币先后抛掷两次,则至少出现一次正面向上的概率为( )
A. B. C. D.
6.一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1,2,3,4.随机抽取一张卡片,然后放回,再随机抽取一张卡片,则两次抽取的卡片上数字之积为偶数的概率是( )
A. B. C. D.
7.如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
A. B. C. D.
8.甲、乙两位同学各抛掷一枚质地均匀的骰子,他们抛掷的点数分别记为a,b,则a+b=9的概率为 .
9.有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3 cm,7 cm,9 cm;乙盒子中装有4张卡片,卡片上分别写着2 cm,4 cm,6 cm,8 cm;盒子外有一张写着5 cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
10.袋子中有红球、白球共10个,这些球除颜色外都相同,将袋中的球搅匀,从中随机摸出一个球,记下颜色后再放回袋中,不断重复这一过程,摸了100次后,发现有30次摸到红球,请你估计这个袋中红球约有 个.
11.现有4张卡片,其中3张卡片正面上的图案是“”,1张卡片正面上的图案是“”,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取2张,则这2张卡片正面图案相同的概率是( )
A. B. C. D.
12.毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小明将这五位名人介绍分别写在五张完全相同的知识卡片上,小亮从中随机抽取一张,卡片上介绍的人物是汉朝以后出生的概率是 .
13.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m-n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
14.“服务他人,提升自我”,来自九年级的5名同学(3男2女)成立了“交通秩序维护”小分队.若从该小分队中任选两名同学进行交通秩序维护,则恰好是一男一女的概率是 .
15.为进一步深化基础教育课程改革,构建符合素质教育要求的学校课程体系,某学校自主开发了A:书法,B:阅读,C:足球,D:器乐四门校本选修课程供学生选择,每门课程被选到的机会均等.
(1)学生小红计划选修两门课程,求她恰好选修书法和器乐的概率;
(2)若学生小明和小刚各计划选修一门课程,则他们两人恰好选修同一门课程的概率为多少?
16.主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重;
B.放下利益,彼此平衡;
C.放下性格,彼此成就;
D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如下两幅不完整的图表.
观点
频数
频率
A
a
0.2
B
12
0.24
C
8
b
D
20
0.4
354330584200
请根据图表中提供的信息,解答下列问题:
(1)参加本次讨论的学生共有 人;
(2)表中a= ,b= ;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.
参考答案:
1.D
2. 随机 .
3.A
4.B
5.C
6.C
7.C
8. .
9.解:(1)画树状图:
共有12种等可能的结果,其中能组成三角形的有7种,
∴P(能组成三角形)=.
(2)∵能与5 cm组成直角三角形的有1种,
∴P(能组成直角三角形)=.
10.3.
11.D
12. .
13.B
14. .
15.解:(1)列表如下:
A
B
C
D
A
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,D)
D
(D,A)
(D,B)
(D,C)
由表格可知,共有12种等可能的结果,其中小红选修书法和器乐的结果有2种,
∴P(小红选修书法和器乐)==.
(2)画树状图如下:
由树状图可知共有16种等可能的结果,其中小明和小刚恰好选修同一门课程的结果有4种,
∴P(小明和小刚恰好选修同一门课程)==.
16.(1)50;
(2)a=10,b=0.16;
解:(3)如图.
(4)画树状图如下:
由树状图可知,共有12种等可能情况,选中观点D(合理竞争,合作双赢)的情况有6种,
∴选中观点D(合理竞争,合作双赢)的概率为=.
同课章节目录
