六年级数学下册课件总复习数与代数数的运算(2)人教版(14张)
文档属性
| 名称 | 六年级数学下册课件总复习数与代数数的运算(2)人教版(14张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览



文档简介
整理和复习
2 数的运算
第2课时 数的运算(2)
——数与代数
一、回顾整理
运算定律
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
文字描述
字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
两数相加,交换加数的位置,它们的和不变
a+b=b+a
三个数相加,先把前两个数相加,再加上第三个数,或者先把后两个数相加,再和第一个数相加,和不变
(a+b)+c=a+(b+c)
两数相乘,交换因数的位置,它们的积不变
a×b=b×a
三个数相乘,先把前两个数相乘,再乘第三个数,或者先把后两个数相乘,再和第一个数相乘,积不变
(a×b)×c=a×(b×c)
两个数的和与一个数相乘,等于把这两个数分别与这个数相乘,再把两个积相加
(a+b)×c=a×c+b×c
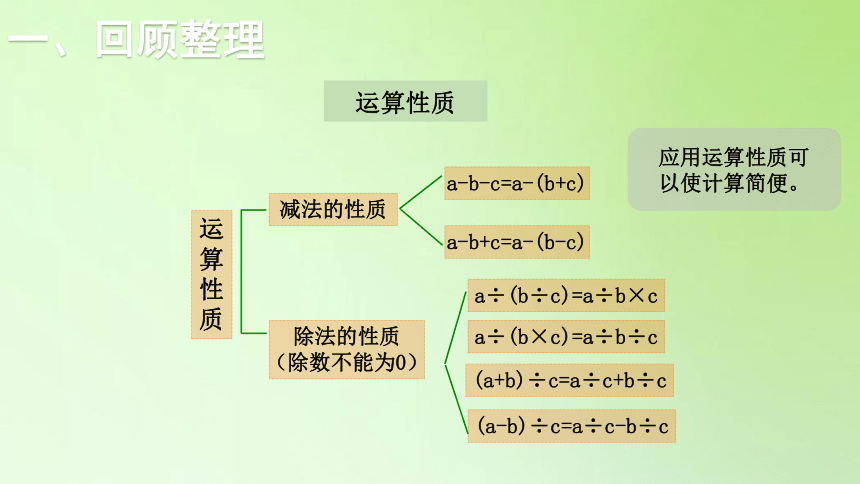
一、回顾整理
运算性质
减法的性质
除法的性质
(除数不能为0)
运
算
性
质
a-b-c=a-(b+c)
a÷(b×c)=a÷b÷c
a-b+c=a-(b-c)
应用运算性质可以使计算简便。
a÷(b÷c)=a÷b×c
(a+b)÷c=a÷c+b÷c
(a-b)÷c=a÷c-b÷c
一、回顾整理
估算
对事物的数量或计算结果作出粗略的推断或估计叫估算。
根据算式中各数的特点,估算时一般将其中较大的数看作与它最接近的整十、整百、整千……的数,使原式通过口算便可求出得数。由于得数是近似值,所以书写结果时要用“≈”连接。
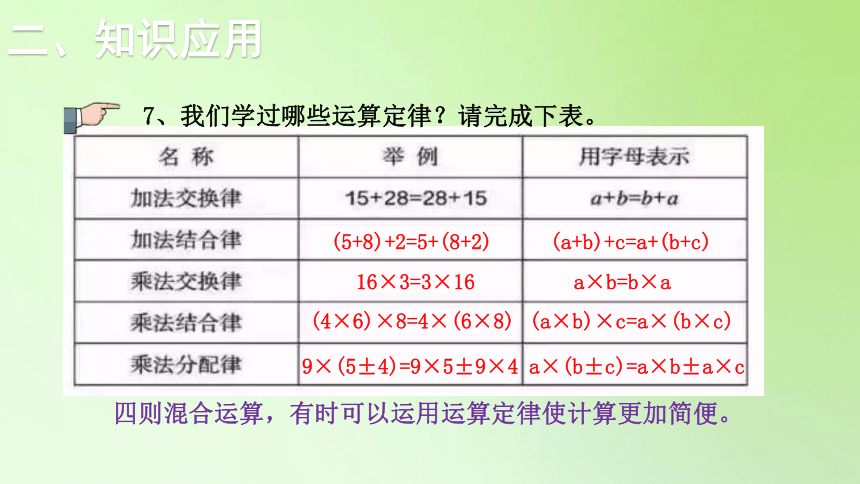
二、知识应用
7、我们学过哪些运算定律?请完成下表。
四则混合运算,有时可以运用运算定律使计算更加简便。
(a+b)+c=a+(b+c)
(5+8)+2=5+(8+2)
a×b=b×a
16×3=3×16
(a×b)×c=a×(b×c)
(4×6)×8=4×(6×8)
a×(b±c)=a×b±a×c
9×(5±4)=9×5±9×4
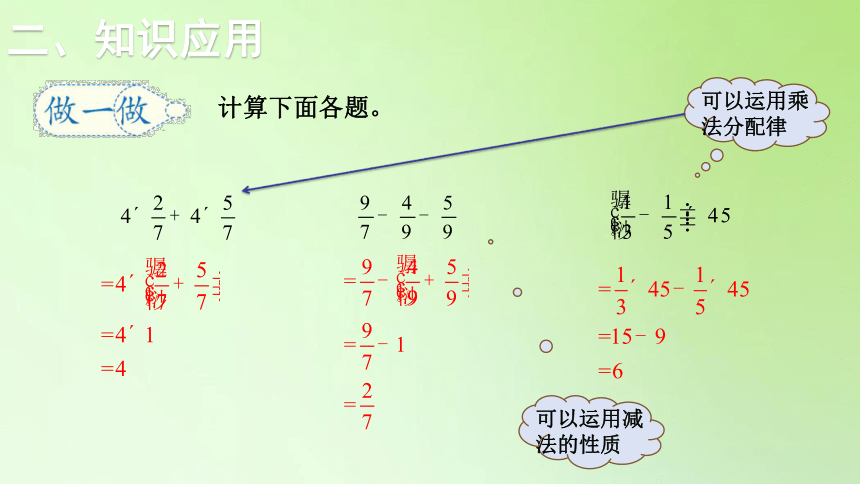
二、知识应用
计算下面各题。
可以运用乘法分配律
可以运用减法的性质
二、知识应用
8、举例说明估算的应用,你知道哪些估算策略?
(1)7.99×9.99与80比,哪个大?
将7.99和9.99分别估算成8和10计算,得乘积为80,由于两个数被估大了,所以它们的乘积比80小。
(2) 比1大吗?
将 估算成 计算,得和为1,由于 被估小了,所以它们的和比1大。
8、举例说明估算的应用,你知道哪些估算策略?
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6元;又花39.6元买了一本汉语词典;之后,妈妈还想买一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪一本?
将20.6估算成21,将39.6估算成40。
二、知识应用
20.6×2=41.2(元)≈41(元)
41+40=81(元)
100-81=19(元)
13.7<19<23.8
答:估算后,妈妈的钱只够买薄本的菜谱。
二、知识应用
六年级有5个班,1至5班的人数依次为:43、40、41、44、42,学校小礼堂有200个座位,如果召开六年级毕业典礼,需要加椅子吗?
因为把43、41、44、42看成40计算时,都把原数看小了,所以这5个数的和的准确值要比近似值200大,说明开会的人数比椅子数多。因此需要加椅子。
答:如果召开六年级毕业典礼,需要加椅子。
三、巩固反馈
5、计算。
59×101 12.7-3.6-5.4 12.5×8÷12.5×8
=5959
=3.7
=64
练
习
十
五
=6+20-21
=5
三、巩固反馈
0.91÷0.3≈( )
41.3×2.5≈( )
70
27
3
100
41.8÷0.6≈( )
3.1×8.9≈( )
3、估算。
四、课堂小结
通过本节课的复习,你对运算律和运算性质又有什么新的体会和收获?
作业:
五、作业布置
2 数的运算
第2课时 数的运算(2)
——数与代数
一、回顾整理
运算定律
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
文字描述
字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
两数相加,交换加数的位置,它们的和不变
a+b=b+a
三个数相加,先把前两个数相加,再加上第三个数,或者先把后两个数相加,再和第一个数相加,和不变
(a+b)+c=a+(b+c)
两数相乘,交换因数的位置,它们的积不变
a×b=b×a
三个数相乘,先把前两个数相乘,再乘第三个数,或者先把后两个数相乘,再和第一个数相乘,积不变
(a×b)×c=a×(b×c)
两个数的和与一个数相乘,等于把这两个数分别与这个数相乘,再把两个积相加
(a+b)×c=a×c+b×c
一、回顾整理
运算性质
减法的性质
除法的性质
(除数不能为0)
运
算
性
质
a-b-c=a-(b+c)
a÷(b×c)=a÷b÷c
a-b+c=a-(b-c)
应用运算性质可以使计算简便。
a÷(b÷c)=a÷b×c
(a+b)÷c=a÷c+b÷c
(a-b)÷c=a÷c-b÷c
一、回顾整理
估算
对事物的数量或计算结果作出粗略的推断或估计叫估算。
根据算式中各数的特点,估算时一般将其中较大的数看作与它最接近的整十、整百、整千……的数,使原式通过口算便可求出得数。由于得数是近似值,所以书写结果时要用“≈”连接。
二、知识应用
7、我们学过哪些运算定律?请完成下表。
四则混合运算,有时可以运用运算定律使计算更加简便。
(a+b)+c=a+(b+c)
(5+8)+2=5+(8+2)
a×b=b×a
16×3=3×16
(a×b)×c=a×(b×c)
(4×6)×8=4×(6×8)
a×(b±c)=a×b±a×c
9×(5±4)=9×5±9×4
二、知识应用
计算下面各题。
可以运用乘法分配律
可以运用减法的性质
二、知识应用
8、举例说明估算的应用,你知道哪些估算策略?
(1)7.99×9.99与80比,哪个大?
将7.99和9.99分别估算成8和10计算,得乘积为80,由于两个数被估大了,所以它们的乘积比80小。
(2) 比1大吗?
将 估算成 计算,得和为1,由于 被估小了,所以它们的和比1大。
8、举例说明估算的应用,你知道哪些估算策略?
(3)妈妈带100元去书店买书,她买了两本文学书,每本20.6元;又花39.6元买了一本汉语词典;之后,妈妈还想买一本家庭菜谱,有两本菜谱可供选择:薄本的13.7元,厚本的23.8元。请帮妈妈估算一下,这时她的钱够买哪一本?
将20.6估算成21,将39.6估算成40。
二、知识应用
20.6×2=41.2(元)≈41(元)
41+40=81(元)
100-81=19(元)
13.7<19<23.8
答:估算后,妈妈的钱只够买薄本的菜谱。
二、知识应用
六年级有5个班,1至5班的人数依次为:43、40、41、44、42,学校小礼堂有200个座位,如果召开六年级毕业典礼,需要加椅子吗?
因为把43、41、44、42看成40计算时,都把原数看小了,所以这5个数的和的准确值要比近似值200大,说明开会的人数比椅子数多。因此需要加椅子。
答:如果召开六年级毕业典礼,需要加椅子。
三、巩固反馈
5、计算。
59×101 12.7-3.6-5.4 12.5×8÷12.5×8
=5959
=3.7
=64
练
习
十
五
=6+20-21
=5
三、巩固反馈
0.91÷0.3≈( )
41.3×2.5≈( )
70
27
3
100
41.8÷0.6≈( )
3.1×8.9≈( )
3、估算。
四、课堂小结
通过本节课的复习,你对运算律和运算性质又有什么新的体会和收获?
作业:
五、作业布置
