六年级数学下册课件 总复习 数与形-人教版(17页ppt)
文档属性
| 名称 | 六年级数学下册课件 总复习 数与形-人教版(17页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 16:58:41 | ||
图片预览





文档简介
整理和复习
第1课时 数与形
——数学思考
一、复习引入
找规律
2021年1月的第一个星期六是2号,那么请大家想一想,第二个、第三个和第四个星期六分别是多少号?
我们知道每个星期是7天,那么利用这个规律,我们很容易就知道2021年1月的第二个、第三个和第四个星期六分别是9号、16号、23号。
二、知识应用
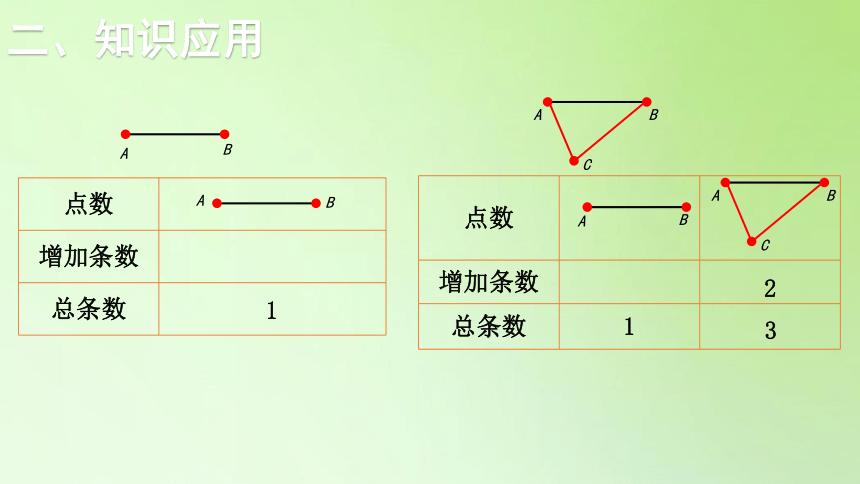
1. 6个点可以连多少条线段?8个点呢?
每两点之间都能连一条线段。
别着急,从2个点开始,逐渐增加点数,找找规律。
二、知识应用
{5940675A-B579-460E-94D1-54222C63F5DA}点数
增加条数
总条数
A
B
A
B
1
{5940675A-B579-460E-94D1-54222C63F5DA}点数
增加条数
总条数
1
A
B
C
A
B
A
B
C
2
3
二、知识应用
{5940675A-B579-460E-94D1-54222C63F5DA}点数
增加条数
2
总条数
1
3
A
B
C
A
B
C
D
A
B
C
D
A
B
3
6
二、知识应用
A
B
C
D
E
{5940675A-B579-460E-94D1-54222C63F5DA}点数
增加
条数
2
3
总条数
1
3
6
A
B
C
D
A
B
C
A
B
C
D
E
A
B
4
10
二、知识应用
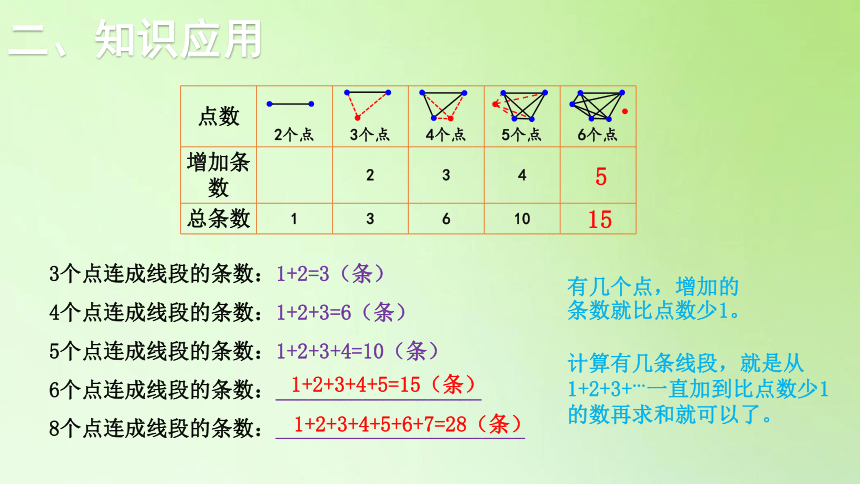
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
5个点连成线段的条数:1+2+3+4=10(条)
6个点连成线段的条数:___________________
8个点连成线段的条数:_______________________
{5940675A-B579-460E-94D1-54222C63F5DA}点数
2个点
3个点
4个点
5个点
6个点
增加条数
2
3
4
总条数
1
3
6
10
1+2+3+4+5=15(条)
5
15
1+2+3+4+5+6+7=28(条)
有几个点,增加的条数就比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
二、知识应用
n个点共连
12个点共连
20个点共连
根据规律,你知道12个点、20个点能连多少条线段吗?请写出算式。想一想,n个点能连多少条线段?
1+2+3+4+5+6+7+8+9+10+11=66(条)
1+2+3+…+19=190(条)
1+2+3+…+(n-1)=n(n-1)÷2
和=(首项+末项)×项数÷2
三、巩固反馈
1. 观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
(1)
(2)
(3)
(4)
7×7=49(个)
15×15=225(个)
答:第7幅图有49个棋子,第15幅图有225个棋子。
三、巩固反馈
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2 =棋子总数
答:第n幅图每边有n个棋子,一共有n2个棋子。
1. 观察下图,想一想。
(2)第 n 幅图有多少个棋子?
(1)
(2)
(3)
(4)
相等
{5940675A-B579-460E-94D1-54222C63F5DA}
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
{5940675A-B579-460E-94D1-54222C63F5DA}
n
n
……
……
三、巩固反馈
1、找规律,填数。
(1)3,11,20,30,_____,53,_____,…
+8
+9
+10
+11
+12
+13
41
66
(2)1,3,2,6,4,9,8,_____,_____,15,____,18,…
12
16
32
练
习
二
十
二
三、巩固反馈
2、摆一摆,找规律。
(1)第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
1+2×7=15(根)
(3)摆第n个图形需要用多少根小棒?
答:摆第7个图形需要用15根小棒。
答:摆第n个图形需要用(2n+1)根小棒。
假设第一个三角形的第一根小棒不动,每增加一个三角形,就增加两根小棒。
(平行四边形)
练
习
二
十
二
三、巩固反馈
3、节日期间广场上有一排彩旗,按照1面红旗、2面黄旗、3面绿旗的顺序排列。第55面彩旗是什么颜色?第100面呢?
故第55面彩旗是红色的。
55÷(1+2+3)=9(组)……1(面),
100÷(1+2+3)=16(组)……4(面),
故第100面彩旗是绿色的。
练
习
二
十
二
三、巩固反馈
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
4.(1)多边形内角和与它的边数有什么关系?
多边形里分成的三角形个数,正好是这个多边形的边数-2。
多边形内角和=(边数-2)×180°
练
习
二
十
二
三、巩固反馈
(2)一个九边形的内角和是多少度?
(3)一个n边形的内角和是多少度?
(9-2)×180°=1260°
(n-2)×180°
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
四、课堂小结
通过这节课,我们发现了一些数与形的规律,通过这些规律,我们能解决一些实际问题。我们知道了世界上的一切事物都有它自己的规律,虽然我们不能去打破她,但我们能够去发现并利用规律。
作业:
五、作业布置
第1课时 数与形
——数学思考
一、复习引入
找规律
2021年1月的第一个星期六是2号,那么请大家想一想,第二个、第三个和第四个星期六分别是多少号?
我们知道每个星期是7天,那么利用这个规律,我们很容易就知道2021年1月的第二个、第三个和第四个星期六分别是9号、16号、23号。
二、知识应用
1. 6个点可以连多少条线段?8个点呢?
每两点之间都能连一条线段。
别着急,从2个点开始,逐渐增加点数,找找规律。
二、知识应用
{5940675A-B579-460E-94D1-54222C63F5DA}点数
增加条数
总条数
A
B
A
B
1
{5940675A-B579-460E-94D1-54222C63F5DA}点数
增加条数
总条数
1
A
B
C
A
B
A
B
C
2
3
二、知识应用
{5940675A-B579-460E-94D1-54222C63F5DA}点数
增加条数
2
总条数
1
3
A
B
C
A
B
C
D
A
B
C
D
A
B
3
6
二、知识应用
A
B
C
D
E
{5940675A-B579-460E-94D1-54222C63F5DA}点数
增加
条数
2
3
总条数
1
3
6
A
B
C
D
A
B
C
A
B
C
D
E
A
B
4
10
二、知识应用
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
5个点连成线段的条数:1+2+3+4=10(条)
6个点连成线段的条数:___________________
8个点连成线段的条数:_______________________
{5940675A-B579-460E-94D1-54222C63F5DA}点数
2个点
3个点
4个点
5个点
6个点
增加条数
2
3
4
总条数
1
3
6
10
1+2+3+4+5=15(条)
5
15
1+2+3+4+5+6+7=28(条)
有几个点,增加的条数就比点数少1。
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和就可以了。
二、知识应用
n个点共连
12个点共连
20个点共连
根据规律,你知道12个点、20个点能连多少条线段吗?请写出算式。想一想,n个点能连多少条线段?
1+2+3+4+5+6+7+8+9+10+11=66(条)
1+2+3+…+19=190(条)
1+2+3+…+(n-1)=n(n-1)÷2
和=(首项+末项)×项数÷2
三、巩固反馈
1. 观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
(1)
(2)
(3)
(4)
7×7=49(个)
15×15=225(个)
答:第7幅图有49个棋子,第15幅图有225个棋子。
三、巩固反馈
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2 =棋子总数
答:第n幅图每边有n个棋子,一共有n2个棋子。
1. 观察下图,想一想。
(2)第 n 幅图有多少个棋子?
(1)
(2)
(3)
(4)
相等
{5940675A-B579-460E-94D1-54222C63F5DA}
图形的序号
每边的棋子数
1
2
1
4
3
2
3
4
{5940675A-B579-460E-94D1-54222C63F5DA}
n
n
……
……
三、巩固反馈
1、找规律,填数。
(1)3,11,20,30,_____,53,_____,…
+8
+9
+10
+11
+12
+13
41
66
(2)1,3,2,6,4,9,8,_____,_____,15,____,18,…
12
16
32
练
习
二
十
二
三、巩固反馈
2、摆一摆,找规律。
(1)第6个图形是什么图形?
(2)摆第7个图形需要用多少根小棒?
1+2×7=15(根)
(3)摆第n个图形需要用多少根小棒?
答:摆第7个图形需要用15根小棒。
答:摆第n个图形需要用(2n+1)根小棒。
假设第一个三角形的第一根小棒不动,每增加一个三角形,就增加两根小棒。
(平行四边形)
练
习
二
十
二
三、巩固反馈
3、节日期间广场上有一排彩旗,按照1面红旗、2面黄旗、3面绿旗的顺序排列。第55面彩旗是什么颜色?第100面呢?
故第55面彩旗是红色的。
55÷(1+2+3)=9(组)……1(面),
100÷(1+2+3)=16(组)……4(面),
故第100面彩旗是绿色的。
练
习
二
十
二
三、巩固反馈
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
4.(1)多边形内角和与它的边数有什么关系?
多边形里分成的三角形个数,正好是这个多边形的边数-2。
多边形内角和=(边数-2)×180°
练
习
二
十
二
三、巩固反馈
(2)一个九边形的内角和是多少度?
(3)一个n边形的内角和是多少度?
(9-2)×180°=1260°
(n-2)×180°
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
四、课堂小结
通过这节课,我们发现了一些数与形的规律,通过这些规律,我们能解决一些实际问题。我们知道了世界上的一切事物都有它自己的规律,虽然我们不能去打破她,但我们能够去发现并利用规律。
作业:
五、作业布置
