六年级数学下册课件-总复习 图形的运动-人教版(18页ppt)
文档属性
| 名称 | 六年级数学下册课件-总复习 图形的运动-人教版(18页ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 00:00:00 | ||
图片预览





文档简介
整理和复习
2 图形的运动
——图形与几何
一、回顾整理
我们学过哪些图形运动的知识?这些图案用到了什么数学知识?
轴对称、平移、旋转、图形的放大与缩小。
一、回顾整理
图形的平移
{5940675A-B579-460E-94D1-54222C63F5DA}
意 义
特 点
要 素
画 法
物体或图形在同一平面内沿直线运动,而本身没有发生方向上的改变,像这样的物体或图形所做的运动叫做平移。
平移不改变图形的大小和形状,只是图形的位置发生变化。
一是平移的方向,二是平移的距离。
要先确定方向,再确定平移的距离。
①平移的方向
图形平移两个关键点:
②平移的距离
一、回顾整理
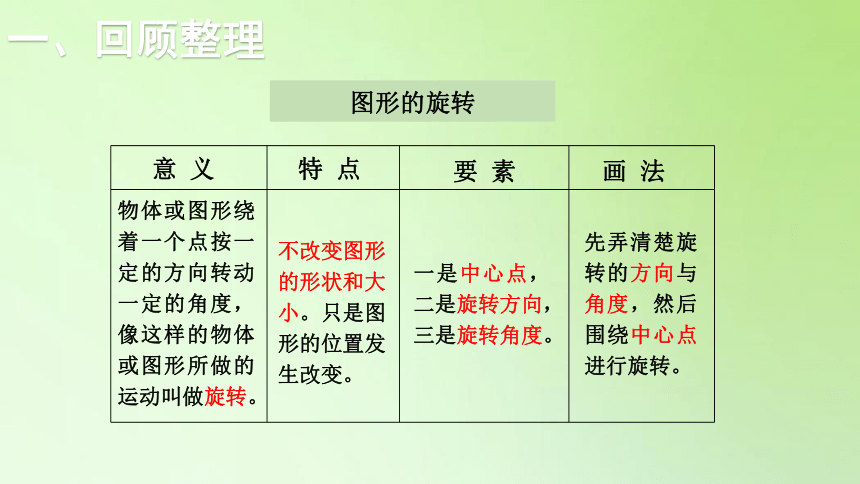
图形的旋转
{5940675A-B579-460E-94D1-54222C63F5DA}
意 义
特 点
要 素
画 法
物体或图形绕着一个点按一定的方向转动一定的角度,像这样的物体或图形所做的运动叫做旋转。
不改变图形的形状和大小。只是图形的位置发生改变。
一是中心点,二是旋转方向,三是旋转角度。
先弄清楚旋转的方向与角度,然后围绕中心点进行旋转。
一、回顾整理
轴对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}
意 义
特 点
画 法
把一个图形沿着某一条直线折叠,如果它能与另一个图形完全重合,那么就说这两个图形关于这条直线对称,叫做轴对称。这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。
对称轴两侧相对的点到对称轴的距离相等。
先确定各对称点的位置,再连线。
注意:平移、旋转和轴对称不改变图形的大小。
一、回顾整理
图形的放大和缩小
可以把一个图形的各边按一定的比进行放大或缩小,从而得到该图形的放大图或缩小图(放大图或缩小图统称为原图形的相似图)。
特征:只改变图形的大小,不改变图形的形状。
一、回顾整理
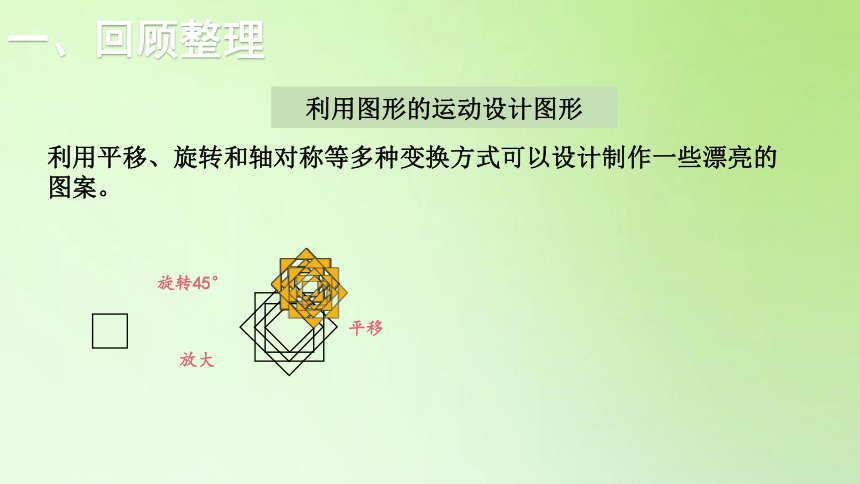
利用图形的运动设计图形
旋转45°
放大
平移
利用平移、旋转和轴对称等多种变换方式可以设计制作一些漂亮的图案。
二、知识应用
1.如图的图案各是从哪张纸上剪下来的?连一连。
二、知识应用
2.图形A是如何变换得到图形B的?
A→B
先向右平移6个格子,
然后再向下平移6格即可得到
二、知识应用
3.画出三角形AOB绕点O点逆时针旋转90°后的图形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
A
B
三、巩固反馈
1、下面哪些图形是轴对称图形?画出它们的对称轴。
第1、2幅图不是轴对称图形,第3、4幅图是轴对称图形。
练
习
十
九
三、巩固反馈
2、根据给定的对称轴画出图形的另一半。
练
习
十
九
3、用圆规和三角尺画出下面的图案。你还能设计什么图案?
三、巩固反馈
还能设计很多好看的图案。
举例:
练
习
十
九
三、巩固反馈
4、下面4个图形的涂色部分面积相等吗?为什么?
相等。因为这4个图形涂色部分的面积都等于一个大圆的面积减去一个中圆的面积,再加上一个小圆的面积。
练
习
十
九
三、巩固反馈
(1)小旗子向左平移8格后的图形。
(2)小旗子绕O点按顺时针方向旋转90°后的图形。
(3)小旗子按2∶1扩大后的图形。
5、画一画。
{5940675A-B579-460E-94D1-54222C63F5DA}
O
{5940675A-B579-460E-94D1-54222C63F5DA}
练
习
十
九
三、巩固反馈
6、一个直角三角形ABC的两条直角边长分别是3cm和4cm,把它按2∶1放大后得到三角形DEF。三角形ABC与DEF的周长之比是多少?面积之比呢?
4
1cm
3
B
A
C
D
E
8
6
CDEF
CABC
∶
=1∶2
=6×8÷2=24(cm2)
SDEF
=3×4÷2=6(cm2)
SABC
∶
=6∶24
=1∶4
SABC
SDEF
答:三角形ABC与DEF的周长之比是1∶2,面积之比是1∶4。
F
练
习
十
九
四、课堂小结
通过本节课的复习,你对图形的运动又有什么新的体会和收获?
作业:
五、作业布置
2 图形的运动
——图形与几何
一、回顾整理
我们学过哪些图形运动的知识?这些图案用到了什么数学知识?
轴对称、平移、旋转、图形的放大与缩小。
一、回顾整理
图形的平移
{5940675A-B579-460E-94D1-54222C63F5DA}
意 义
特 点
要 素
画 法
物体或图形在同一平面内沿直线运动,而本身没有发生方向上的改变,像这样的物体或图形所做的运动叫做平移。
平移不改变图形的大小和形状,只是图形的位置发生变化。
一是平移的方向,二是平移的距离。
要先确定方向,再确定平移的距离。
①平移的方向
图形平移两个关键点:
②平移的距离
一、回顾整理
图形的旋转
{5940675A-B579-460E-94D1-54222C63F5DA}
意 义
特 点
要 素
画 法
物体或图形绕着一个点按一定的方向转动一定的角度,像这样的物体或图形所做的运动叫做旋转。
不改变图形的形状和大小。只是图形的位置发生改变。
一是中心点,二是旋转方向,三是旋转角度。
先弄清楚旋转的方向与角度,然后围绕中心点进行旋转。
一、回顾整理
轴对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}
意 义
特 点
画 法
把一个图形沿着某一条直线折叠,如果它能与另一个图形完全重合,那么就说这两个图形关于这条直线对称,叫做轴对称。这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。
对称轴两侧相对的点到对称轴的距离相等。
先确定各对称点的位置,再连线。
注意:平移、旋转和轴对称不改变图形的大小。
一、回顾整理
图形的放大和缩小
可以把一个图形的各边按一定的比进行放大或缩小,从而得到该图形的放大图或缩小图(放大图或缩小图统称为原图形的相似图)。
特征:只改变图形的大小,不改变图形的形状。
一、回顾整理
利用图形的运动设计图形
旋转45°
放大
平移
利用平移、旋转和轴对称等多种变换方式可以设计制作一些漂亮的图案。
二、知识应用
1.如图的图案各是从哪张纸上剪下来的?连一连。
二、知识应用
2.图形A是如何变换得到图形B的?
A→B
先向右平移6个格子,
然后再向下平移6格即可得到
二、知识应用
3.画出三角形AOB绕点O点逆时针旋转90°后的图形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
A
B
三、巩固反馈
1、下面哪些图形是轴对称图形?画出它们的对称轴。
第1、2幅图不是轴对称图形,第3、4幅图是轴对称图形。
练
习
十
九
三、巩固反馈
2、根据给定的对称轴画出图形的另一半。
练
习
十
九
3、用圆规和三角尺画出下面的图案。你还能设计什么图案?
三、巩固反馈
还能设计很多好看的图案。
举例:
练
习
十
九
三、巩固反馈
4、下面4个图形的涂色部分面积相等吗?为什么?
相等。因为这4个图形涂色部分的面积都等于一个大圆的面积减去一个中圆的面积,再加上一个小圆的面积。
练
习
十
九
三、巩固反馈
(1)小旗子向左平移8格后的图形。
(2)小旗子绕O点按顺时针方向旋转90°后的图形。
(3)小旗子按2∶1扩大后的图形。
5、画一画。
{5940675A-B579-460E-94D1-54222C63F5DA}
O
{5940675A-B579-460E-94D1-54222C63F5DA}
练
习
十
九
三、巩固反馈
6、一个直角三角形ABC的两条直角边长分别是3cm和4cm,把它按2∶1放大后得到三角形DEF。三角形ABC与DEF的周长之比是多少?面积之比呢?
4
1cm
3
B
A
C
D
E
8
6
CDEF
CABC
∶
=1∶2
=6×8÷2=24(cm2)
SDEF
=3×4÷2=6(cm2)
SABC
∶
=6∶24
=1∶4
SABC
SDEF
答:三角形ABC与DEF的周长之比是1∶2,面积之比是1∶4。
F
练
习
十
九
四、课堂小结
通过本节课的复习,你对图形的运动又有什么新的体会和收获?
作业:
五、作业布置
