六年级数学下册课件-总复习 第4课时 图形的认识与测量(练习课)-人教版(17页ppt)
文档属性
| 名称 | 六年级数学下册课件-总复习 第4课时 图形的认识与测量(练习课)-人教版(17页ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 00:00:00 | ||
图片预览




文档简介
整理和复习
1 图形的认识与测量
第4课时 练习课
——图形与几何
一、基础练习
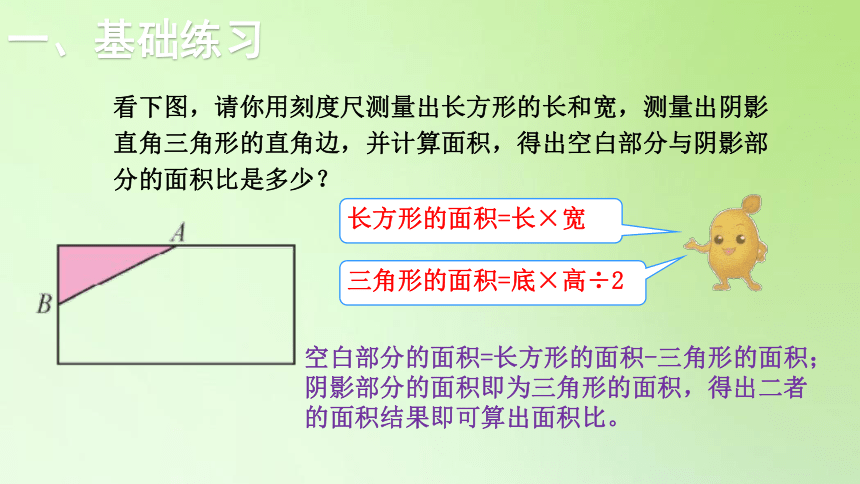
看下图,请你用刻度尺测量出长方形的长和宽,测量出阴影直角三角形的直角边,并计算面积,得出空白部分与阴影部分的面积比是多少?
长方形的面积=长×宽
三角形的面积=底×高÷2
空白部分的面积=长方形的面积-三角形的面积;
阴影部分的面积即为三角形的面积,得出二者的面积结果即可算出面积比。
二、指导练习
1、判断对错,对的画“√”,错的画“×”。
(1)大于90°的角就是钝角。 ( )
(2)两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。 ( )
(3)任何两个等底等高的梯形都能拼成一个平行四边形。
( )
√
×
×
钝角大于90°,小于180°
等底等高不代表形状相同,因此不一定能拼成平行四边形。
练
习
十
八
二、指导练习
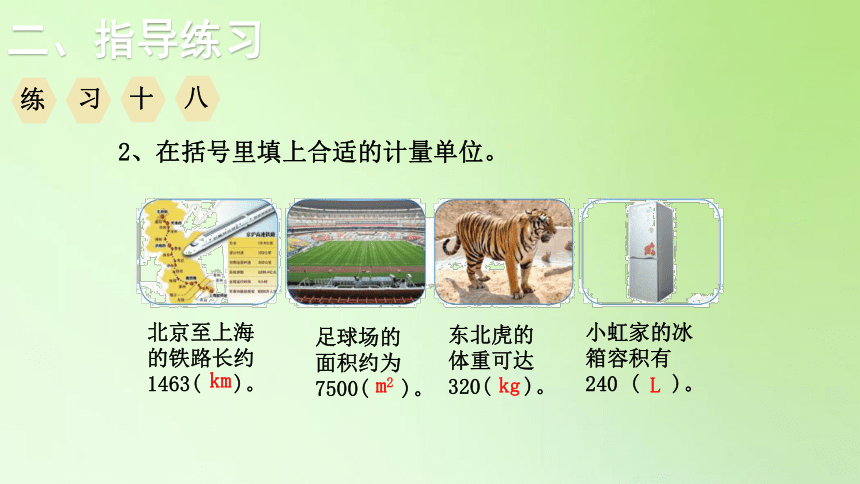
2、在括号里填上合适的计量单位。
北京至上海的铁路长约1463( )。
足球场的面积约为7500( )。
东北虎的体重可达320( )。
小虹家的冰箱容积有240 ( )。
km
kg
m2
L
练
习
十
八
二、指导练习
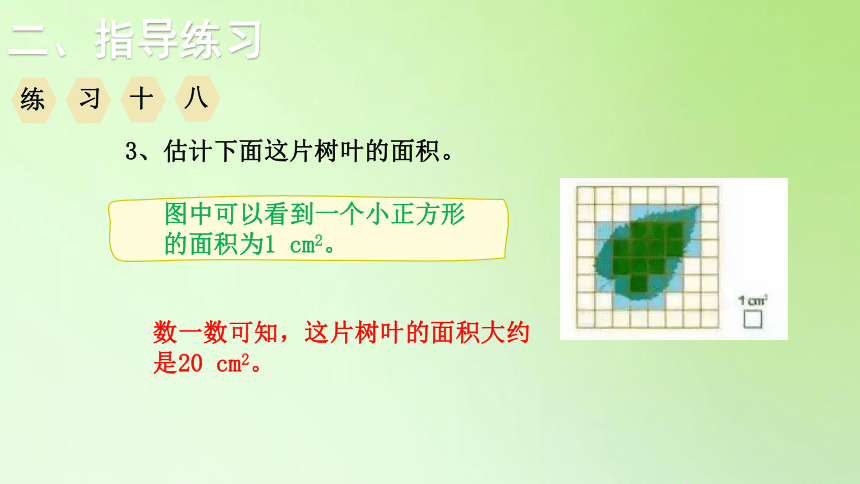
3、估计下面这片树叶的面积。
图中可以看到一个小正方形的面积为1 cm2。
数一数可知,这片树叶的面积大约是20 cm2。
练
习
十
八
二、指导练习
4、每一组中两个图形的周长相等吗?面积呢?
长方形和平行四边形面积相等,周长不等。
周长相等,面积不等。
两个平面图形的面积相等,周长不一定相等。
两个平面图形的周长相等,面积不一定相等。
练
习
十
八
二、指导练习
7、在长12.4cm、宽7.2cm的长方形纸中,剪半径是1cm的圆,能剪多少个?画一画,剪一剪。
可以把长方形纸划分为边长2cm的正方形,则一行有6个,有这样的3行,共有18个正方形,每个正方形里可以剪出一个符合要求的圆,即可剪18个圆。
若第一行画出6个圆,第二行的圆可以同时和第一行的两个圆相切,则第二行可以剪出5个这样的圆,这样宽7.2cm的长方形可以剪出四行这样的圆。6+5+6+5=22(个)。
练
习
十
八
在长方形纸上剪圆,圆和圆就算挨在一起必然还会有间隙,产生废纸,所以用长方形的面积除以一个圆的面积得出的28个,是剪不出来的。
只能画18个。
能画28个。
12、把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米。)
V =103=1000(cm3)
正方体
V = πr2h
圆锥
答:这个圆锥形铁块的高约是10cm。
正方体铁块变成圆锥形铁块,形状变了,前后体积没变。
h=1000×3÷π÷(20÷2)2≈10(cm)
二、指导练习
练
习
十
八
二、指导练习
16、一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
3.14×10=31.4(cm2)
正方形的面积是10,
圆半径的平方就是10。
答:涂色部分的面积是7.85 cm2。
31.4× =7.85(cm2)
练
习
十
八
二、指导练习
17、用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围用纸最多?
用纸最多就是表面积最大。
棱长:24÷12=2(cm)
表面积:2×2×6=24(cm2)
围成正方体
棱长之和:24÷4=6(cm)
假设长为3cm,宽为2cm,高为1cm,
表面积:
3×2×2+3×1×2+2×1×2=22(cm2)
围成长方体
答:围成正方体用纸多,最多是24 cm2。
24>22
练
习
十
八
三、巩固练习
1、填空。
(1)边长是8cm的正方形,面积是( )cm2。
(2)将棱长是3m的正方体木箱放在地上,占地面积为( )m2,和它等体积的长方体木箱面积是12m2,高是( )m。
(3)一个圆的直径是16cm,圆的面积是( )cm2。
(4)将18个相同的铁圆锥,可以熔铸成( )个和它们等底等高的圆柱。
(5)把一个圆柱的侧面展开后,得到一个长方形,长方形的长6.28cm,宽是3.14cm,这个圆柱的底面半径是( )cm。
64
200.96
2.25
9
6
1或0.5
三、巩固练习
2、判断。
(1)正方形是特殊的长方形。 ( )
(2)正方体、长方体、圆柱和圆锥都可以用公式V=Sh求体积。( )
(3)两个圆的面积相等,它们的周长也一定相等。 ( )
√
√
×
三、巩固练习
3、解决问题。
答:它的体积是15.625 cm3。
(1)正方体的棱长扩大到原来的2倍,它的表面积扩大到原来的多少倍?如果原来的正方体棱长是25dm,它的体积是多少立方米?
25 dm=2.5 m 2.5×2.5×2.5=15.625(cm3)
它的表面积扩大到原来的4倍。
三、巩固练习
3.14×(6÷2+1)2-3.14×(6÷2)2
=21.98(cm2)
(2)一个圆环,内圆直径是6cm,环宽1cm,那么圆环的面积是多少平方厘米?
答:圆环的面积是21.98 cm2。
3、解决问题。
答:它的体积是2392.5 cm3。
(3)根据图中尺寸,求出下面物体的体积。(注:长方体的底面为正方形,单位:cm)
20×20×5+ ×3.14×(10÷2)2×(20-5) =2392.5(cm3)
三、巩固练习
3、解决问题。
四、课堂小结
通过本课时的学习,请你说一说对图形的认识和测量过程中有哪些需要注意的地方,我们怎样可以将图形画得又快又好。
作业:
五、作业布置
1 图形的认识与测量
第4课时 练习课
——图形与几何
一、基础练习
看下图,请你用刻度尺测量出长方形的长和宽,测量出阴影直角三角形的直角边,并计算面积,得出空白部分与阴影部分的面积比是多少?
长方形的面积=长×宽
三角形的面积=底×高÷2
空白部分的面积=长方形的面积-三角形的面积;
阴影部分的面积即为三角形的面积,得出二者的面积结果即可算出面积比。
二、指导练习
1、判断对错,对的画“√”,错的画“×”。
(1)大于90°的角就是钝角。 ( )
(2)两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。 ( )
(3)任何两个等底等高的梯形都能拼成一个平行四边形。
( )
√
×
×
钝角大于90°,小于180°
等底等高不代表形状相同,因此不一定能拼成平行四边形。
练
习
十
八
二、指导练习
2、在括号里填上合适的计量单位。
北京至上海的铁路长约1463( )。
足球场的面积约为7500( )。
东北虎的体重可达320( )。
小虹家的冰箱容积有240 ( )。
km
kg
m2
L
练
习
十
八
二、指导练习
3、估计下面这片树叶的面积。
图中可以看到一个小正方形的面积为1 cm2。
数一数可知,这片树叶的面积大约是20 cm2。
练
习
十
八
二、指导练习
4、每一组中两个图形的周长相等吗?面积呢?
长方形和平行四边形面积相等,周长不等。
周长相等,面积不等。
两个平面图形的面积相等,周长不一定相等。
两个平面图形的周长相等,面积不一定相等。
练
习
十
八
二、指导练习
7、在长12.4cm、宽7.2cm的长方形纸中,剪半径是1cm的圆,能剪多少个?画一画,剪一剪。
可以把长方形纸划分为边长2cm的正方形,则一行有6个,有这样的3行,共有18个正方形,每个正方形里可以剪出一个符合要求的圆,即可剪18个圆。
若第一行画出6个圆,第二行的圆可以同时和第一行的两个圆相切,则第二行可以剪出5个这样的圆,这样宽7.2cm的长方形可以剪出四行这样的圆。6+5+6+5=22(个)。
练
习
十
八
在长方形纸上剪圆,圆和圆就算挨在一起必然还会有间隙,产生废纸,所以用长方形的面积除以一个圆的面积得出的28个,是剪不出来的。
只能画18个。
能画28个。
12、把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米。)
V =103=1000(cm3)
正方体
V = πr2h
圆锥
答:这个圆锥形铁块的高约是10cm。
正方体铁块变成圆锥形铁块,形状变了,前后体积没变。
h=1000×3÷π÷(20÷2)2≈10(cm)
二、指导练习
练
习
十
八
二、指导练习
16、一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
3.14×10=31.4(cm2)
正方形的面积是10,
圆半径的平方就是10。
答:涂色部分的面积是7.85 cm2。
31.4× =7.85(cm2)
练
习
十
八
二、指导练习
17、用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围用纸最多?
用纸最多就是表面积最大。
棱长:24÷12=2(cm)
表面积:2×2×6=24(cm2)
围成正方体
棱长之和:24÷4=6(cm)
假设长为3cm,宽为2cm,高为1cm,
表面积:
3×2×2+3×1×2+2×1×2=22(cm2)
围成长方体
答:围成正方体用纸多,最多是24 cm2。
24>22
练
习
十
八
三、巩固练习
1、填空。
(1)边长是8cm的正方形,面积是( )cm2。
(2)将棱长是3m的正方体木箱放在地上,占地面积为( )m2,和它等体积的长方体木箱面积是12m2,高是( )m。
(3)一个圆的直径是16cm,圆的面积是( )cm2。
(4)将18个相同的铁圆锥,可以熔铸成( )个和它们等底等高的圆柱。
(5)把一个圆柱的侧面展开后,得到一个长方形,长方形的长6.28cm,宽是3.14cm,这个圆柱的底面半径是( )cm。
64
200.96
2.25
9
6
1或0.5
三、巩固练习
2、判断。
(1)正方形是特殊的长方形。 ( )
(2)正方体、长方体、圆柱和圆锥都可以用公式V=Sh求体积。( )
(3)两个圆的面积相等,它们的周长也一定相等。 ( )
√
√
×
三、巩固练习
3、解决问题。
答:它的体积是15.625 cm3。
(1)正方体的棱长扩大到原来的2倍,它的表面积扩大到原来的多少倍?如果原来的正方体棱长是25dm,它的体积是多少立方米?
25 dm=2.5 m 2.5×2.5×2.5=15.625(cm3)
它的表面积扩大到原来的4倍。
三、巩固练习
3.14×(6÷2+1)2-3.14×(6÷2)2
=21.98(cm2)
(2)一个圆环,内圆直径是6cm,环宽1cm,那么圆环的面积是多少平方厘米?
答:圆环的面积是21.98 cm2。
3、解决问题。
答:它的体积是2392.5 cm3。
(3)根据图中尺寸,求出下面物体的体积。(注:长方体的底面为正方形,单位:cm)
20×20×5+ ×3.14×(10÷2)2×(20-5) =2392.5(cm3)
三、巩固练习
3、解决问题。
四、课堂小结
通过本课时的学习,请你说一说对图形的认识和测量过程中有哪些需要注意的地方,我们怎样可以将图形画得又快又好。
作业:
五、作业布置
