六年级数学下册课件总复习图形与几何立体图形人教版(14张)
文档属性
| 名称 | 六年级数学下册课件总复习图形与几何立体图形人教版(14张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览



文档简介
整理和复习
1 图形的认识与测量
第3课时 立体图形
——图形与几何
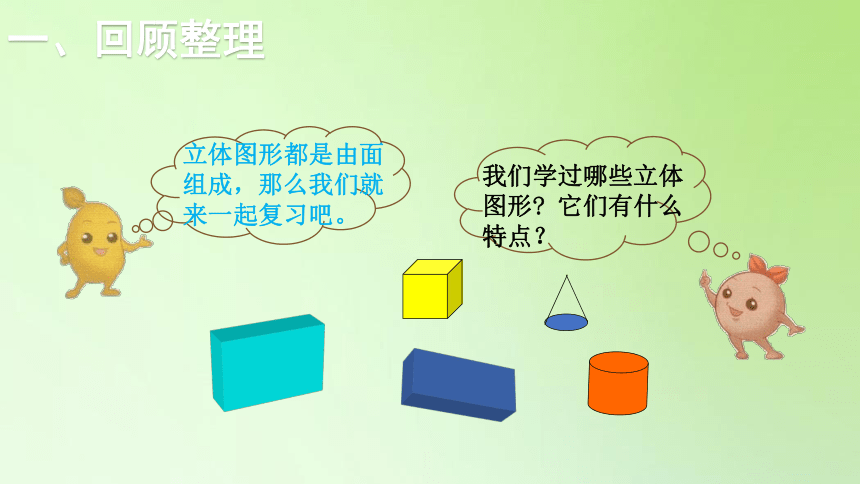
一、回顾整理
我们学过哪些立体图形? 它们有什么特点?
立体图形都是由面组成,那么我们就来一起复习吧。
一、回顾整理
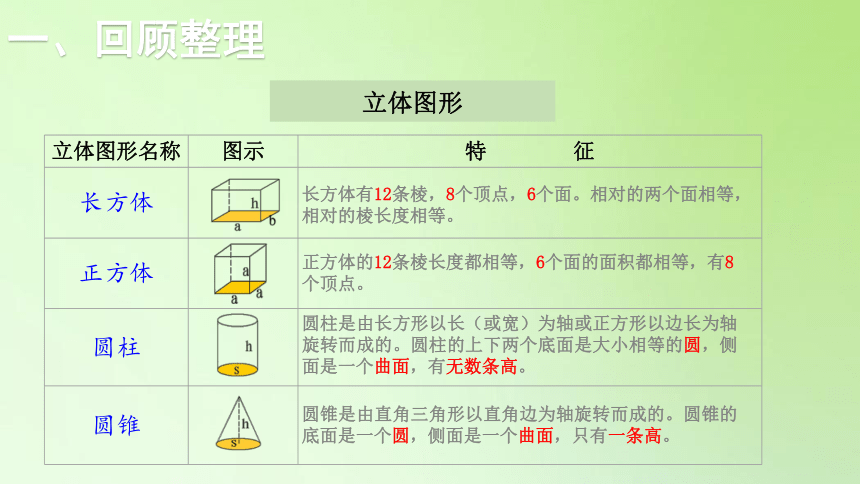
立体图形
{5940675A-B579-460E-94D1-54222C63F5DA}立体图形名称
图示
特 征
长方体
正方体
圆柱
圆锥
长方体有12条棱,8个顶点,6个面。相对的两个面相等,相对的棱长度相等。
正方体的12条棱长度都相等,6个面的面积都相等,有8个顶点。
圆柱是由长方形以长(或宽)为轴或正方形以边长为轴旋转而成的。圆柱的上下两个底面是大小相等的圆,侧面是一个曲面,有无数条高。
圆锥是由直角三角形以直角边为轴旋转而成的。圆锥的底面是一个圆,侧面是一个曲面,只有一条高。
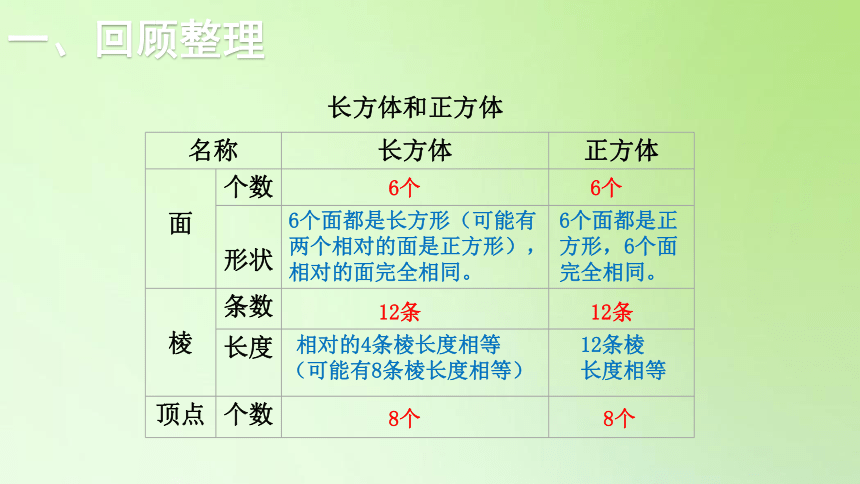
长方体和正方体
{5940675A-B579-460E-94D1-54222C63F5DA}名称
长方体
正方体
面
个数
形状
棱
条数
长度
顶点
个数
6个
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
12条
相对的4条棱长度相等(可能有8条棱长度相等)
6个
6个面都是正方形,6个面完全相同。
12条
12条棱长度相等
8个
8个
一、回顾整理
一、回顾整理
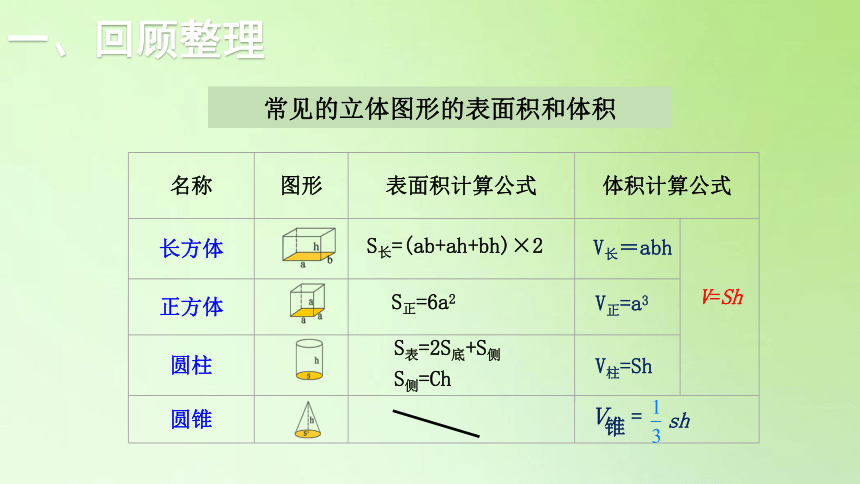
常见的立体图形的表面积和体积
{5940675A-B579-460E-94D1-54222C63F5DA}名称
图形
表面积计算公式
体积计算公式
长方体
正方体
圆柱
圆锥
S长=(ab+ah+bh)×2
S正=6a2
S表=2S底+S侧
S侧=Ch
V长=abh
V正=a3
V柱=Sh
V=Sh
Ⅴ =
锥
sh
二、知识应用
在量杯里放一些水,记下水面的刻度V1,再把马铃薯浸入水中,保证其中的水未溢出且马铃薯完全浸没在水中,记下放入马铃薯后量杯中水面的刻度V2,则V2-V1就是马铃薯的体积。
1、怎样测量一个马铃薯的体积?
二、知识应用
11、把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方形的表面积增加了多少?
V大正方体=63=216(cm3)
V小正方体=23=8(cm3)
216÷8=27(个)
S大正方体=6×62=216(cm2)
S小正方体=6×22=24(cm2)
24×27-216=432(cm2)
12×62=432(cm2)
答:可以得到27个小正方体。它们的表面积之和比原来大正方形的表面积增加432cm2。
沿长、宽、高三个方向各切2次,共切6次,每切一次增加2个大正方形的面积,共增加12个大正方形的面积。
练
习
十
八
二、知识应用
13、在仓库里有一堆存放货物的正方体纸箱,从三个不同方位看到的形状图如下。
这堆货物可能有10箱,也可能有9箱。
这堆货物可能有多少箱?用学具摆一摆。
练
习
十
八
二、知识应用
14、这只工具箱的下半部是棱长为20cm的正方体,上半部是圆柱的一半。算出它的表面积和体积。
表面积:
20×20×5+3.14×20×20÷2+3.14×(20÷2)2
= 2942(cm2)
答:它的表面积是2942 cm2,它的体积是11140 cm3。
体积:
20×20×20+3.14×(20÷2)2×20÷2
= 11140(cm3)
练
习
十
八
三、巩固反馈
1、填空。
(1)用一根96cm的铁丝围成一个正方体,这个正方体的棱长是( )cm,表面积是( )cm2。
(2)一个长方体的长、宽、高都扩大到原来的3倍,那么它的表面积就扩大到原来的( )倍。
(3)如图,这是一个圆锥和一个圆柱
(单位:m),则V圆锥∶V圆柱=( )。
8
384
9
1∶24
三、巩固反馈
2、做一个底面直径是4dm、高是7dm的圆柱形无盖铁皮水桶,大约需要多少平方分米的铁皮?
3.14×(4÷2)2+3.14×4×7
=100.48(dm2)
答:大约需要100.48 dm2的铁皮。
想一想:这个水桶是什么样的,它由哪几面组成?
无盖的铁皮水桶,它是由一个底面和一个侧面组成。
2????r
?
×高
????r2
?
=
+
圆柱表面积
3、把19个棱长为2cm的正方体堆成下图所示的立体图形,这个立体图形的体积和表面积分别是多少?
三、巩固反馈
体积V=19×2×2×2=152(cm3)
表面积S=2×2×(9+8+10)×2=216(cm2)
答:这个立体图形的体积是152 cm3,表面积是216 cm2。
四、课堂小结
通过本节课的复习,你对立体图形又有什么新的体会和收获?
作业:
五、作业布置
1 图形的认识与测量
第3课时 立体图形
——图形与几何
一、回顾整理
我们学过哪些立体图形? 它们有什么特点?
立体图形都是由面组成,那么我们就来一起复习吧。
一、回顾整理
立体图形
{5940675A-B579-460E-94D1-54222C63F5DA}立体图形名称
图示
特 征
长方体
正方体
圆柱
圆锥
长方体有12条棱,8个顶点,6个面。相对的两个面相等,相对的棱长度相等。
正方体的12条棱长度都相等,6个面的面积都相等,有8个顶点。
圆柱是由长方形以长(或宽)为轴或正方形以边长为轴旋转而成的。圆柱的上下两个底面是大小相等的圆,侧面是一个曲面,有无数条高。
圆锥是由直角三角形以直角边为轴旋转而成的。圆锥的底面是一个圆,侧面是一个曲面,只有一条高。
长方体和正方体
{5940675A-B579-460E-94D1-54222C63F5DA}名称
长方体
正方体
面
个数
形状
棱
条数
长度
顶点
个数
6个
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
12条
相对的4条棱长度相等(可能有8条棱长度相等)
6个
6个面都是正方形,6个面完全相同。
12条
12条棱长度相等
8个
8个
一、回顾整理
一、回顾整理
常见的立体图形的表面积和体积
{5940675A-B579-460E-94D1-54222C63F5DA}名称
图形
表面积计算公式
体积计算公式
长方体
正方体
圆柱
圆锥
S长=(ab+ah+bh)×2
S正=6a2
S表=2S底+S侧
S侧=Ch
V长=abh
V正=a3
V柱=Sh
V=Sh
Ⅴ =
锥
sh
二、知识应用
在量杯里放一些水,记下水面的刻度V1,再把马铃薯浸入水中,保证其中的水未溢出且马铃薯完全浸没在水中,记下放入马铃薯后量杯中水面的刻度V2,则V2-V1就是马铃薯的体积。
1、怎样测量一个马铃薯的体积?
二、知识应用
11、把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方形的表面积增加了多少?
V大正方体=63=216(cm3)
V小正方体=23=8(cm3)
216÷8=27(个)
S大正方体=6×62=216(cm2)
S小正方体=6×22=24(cm2)
24×27-216=432(cm2)
12×62=432(cm2)
答:可以得到27个小正方体。它们的表面积之和比原来大正方形的表面积增加432cm2。
沿长、宽、高三个方向各切2次,共切6次,每切一次增加2个大正方形的面积,共增加12个大正方形的面积。
练
习
十
八
二、知识应用
13、在仓库里有一堆存放货物的正方体纸箱,从三个不同方位看到的形状图如下。
这堆货物可能有10箱,也可能有9箱。
这堆货物可能有多少箱?用学具摆一摆。
练
习
十
八
二、知识应用
14、这只工具箱的下半部是棱长为20cm的正方体,上半部是圆柱的一半。算出它的表面积和体积。
表面积:
20×20×5+3.14×20×20÷2+3.14×(20÷2)2
= 2942(cm2)
答:它的表面积是2942 cm2,它的体积是11140 cm3。
体积:
20×20×20+3.14×(20÷2)2×20÷2
= 11140(cm3)
练
习
十
八
三、巩固反馈
1、填空。
(1)用一根96cm的铁丝围成一个正方体,这个正方体的棱长是( )cm,表面积是( )cm2。
(2)一个长方体的长、宽、高都扩大到原来的3倍,那么它的表面积就扩大到原来的( )倍。
(3)如图,这是一个圆锥和一个圆柱
(单位:m),则V圆锥∶V圆柱=( )。
8
384
9
1∶24
三、巩固反馈
2、做一个底面直径是4dm、高是7dm的圆柱形无盖铁皮水桶,大约需要多少平方分米的铁皮?
3.14×(4÷2)2+3.14×4×7
=100.48(dm2)
答:大约需要100.48 dm2的铁皮。
想一想:这个水桶是什么样的,它由哪几面组成?
无盖的铁皮水桶,它是由一个底面和一个侧面组成。
2????r
?
×高
????r2
?
=
+
圆柱表面积
3、把19个棱长为2cm的正方体堆成下图所示的立体图形,这个立体图形的体积和表面积分别是多少?
三、巩固反馈
体积V=19×2×2×2=152(cm3)
表面积S=2×2×(9+8+10)×2=216(cm2)
答:这个立体图形的体积是152 cm3,表面积是216 cm2。
四、课堂小结
通过本节课的复习,你对立体图形又有什么新的体会和收获?
作业:
五、作业布置
