六年级数学下册课件总复习图形与几何平面图形的认识人教版(13张)
文档属性
| 名称 | 六年级数学下册课件总复习图形与几何平面图形的认识人教版(13张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览

文档简介
整理和复习
1 图形的认识与测量
第1课时 平面图形的认识
——图形与几何
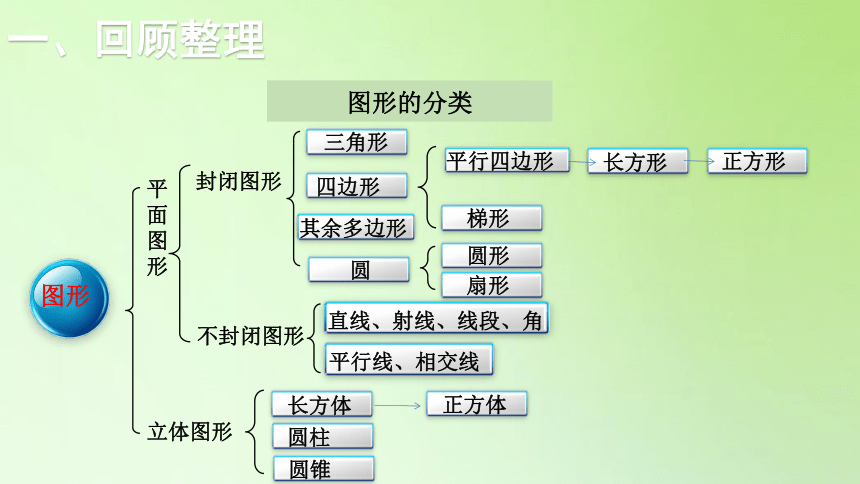
一、回顾整理
图形的分类
封闭图形
不封闭图形
直线、射线、线段、角
图形
长方形
圆
正方形
平行四边形
梯形
三角形
立体图形
平行线、相交线
平面图形
四边形
其余多边形
长方体
圆柱
圆锥
正方体
圆形
扇形
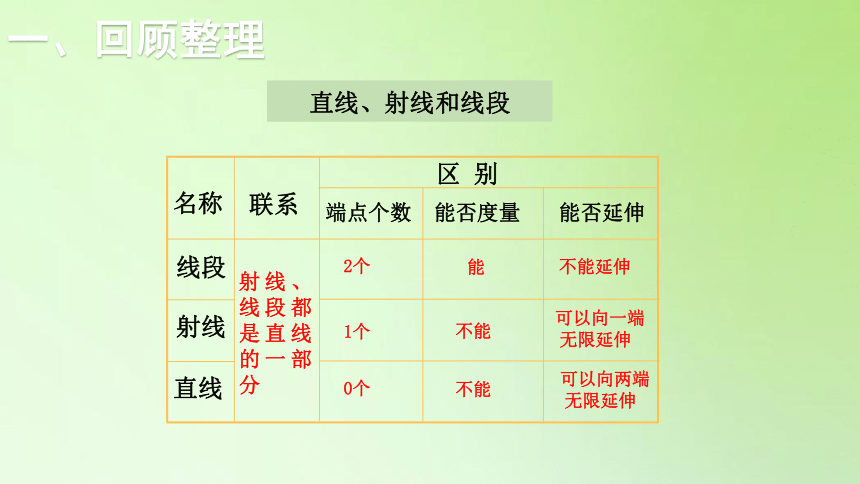
一、回顾整理
直线、射线和线段
射线
线段
直线
区 别
联系
名称
能否延伸
能
不能
不能
能否度量
1个
0个
射线、线段都是直线的一部分
端点个数
2个
可以向两端无限延伸
不能延伸
可以向一端 无限延伸
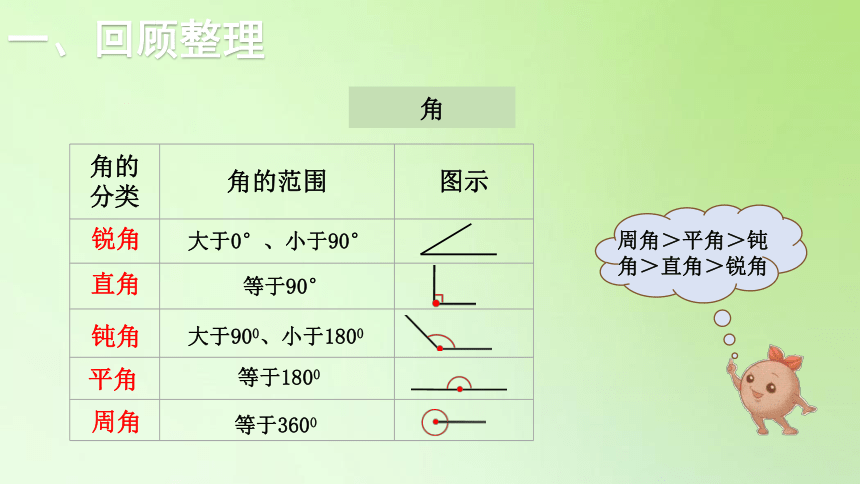
一、回顾整理
角
{5940675A-B579-460E-94D1-54222C63F5DA}角的
分类
角的范围
图示
锐角
大于0°、小于90°
直角
等于90°
钝角
大于900、小于1800
等于1800
等于3600
周角>平角>钝角>直角>锐角
平角
周角
一、回顾整理
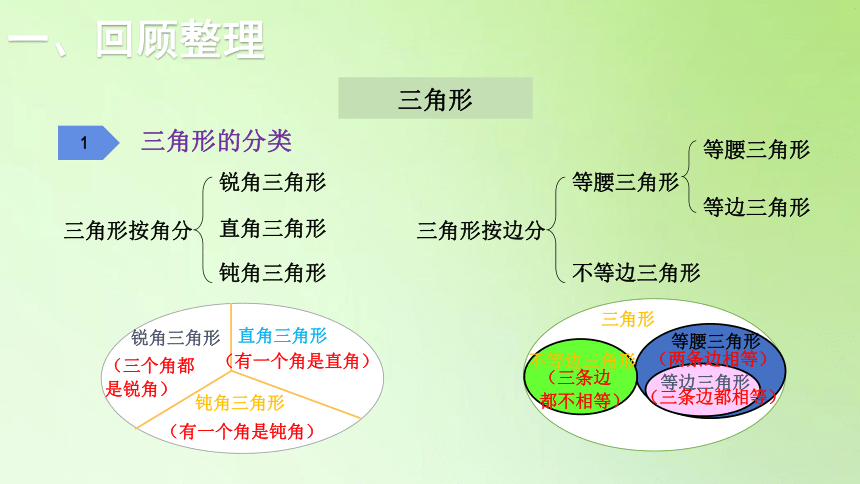
三角形
三角形的分类
三角形按角分
锐角三角形
直角三角形
钝角三角形
(三个角都是锐角)
(有一个角是直角)
(有一个角是钝角)
1
锐角三角形
直角三角形
钝角三角形
三角形按边分
等腰三角形
等腰三角形
不等边三角形
等边三角形
三角形
等腰三角形
等边三角形
(两条边相等)
(三条边都相等)
不等边三角形
(三条边都不相等)
一、回顾整理
三角形
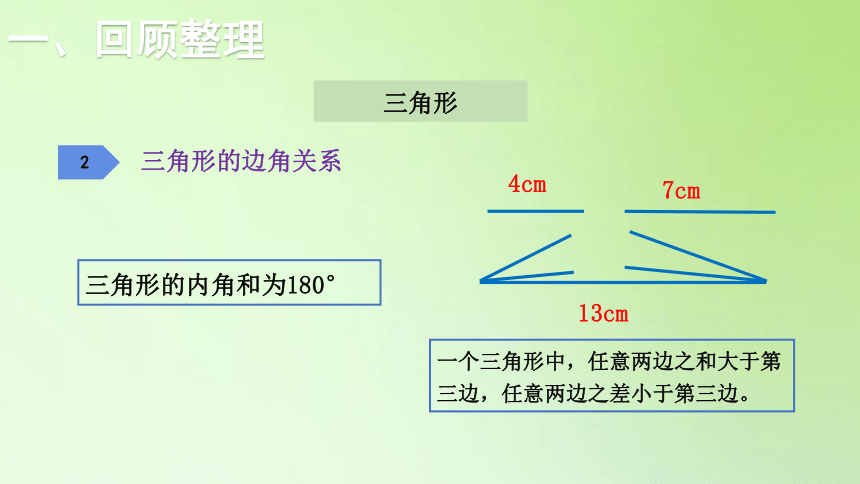
三角形的内角和为180°
一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
三角形的边角关系
2
13cm
4cm
7cm
一、回顾整理
四边形
四边形的分类
四边形
平行四边形
长方形
正方形
梯形
等腰梯形
直角梯形
1
一、回顾整理
四边形
常见的四边形及其特征
{5940675A-B579-460E-94D1-54222C63F5DA}名称
图例
特征
平行四边形
长方形
正方形
梯形
等腰梯形
直角梯形
两腰相等
两组对边分别平行且相等
只有一组对边平行
(1)两组对边分别平行且相等;(2)四个角都是直角
(1)两组对边分别平行;(2)四条边相等;(3)四个角都是直角
有两个角是直角
2
一、回顾整理
圆
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}圆的定义
圆各部分
的名称
圆的特点
圆是一种封闭的曲线图形
(1)圆心:圆中心的一点叫做圆心,如图,点O是圆心。
(2)半径:连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示。
(3)直径:通过圆心且两端都在圆上的线段叫做直径,一般用字母d表示
(1)圆心确定圆的位置,半径决定圆的大小。
(2)同圆或等圆中,半径是直径的一半,直径是半径的2倍。
(3)圆是轴对称图形,圆的直径所在的直线是它的对称轴,它有无数条对称轴
二、知识应用
做两个一样的平行四边形纸片。把它们重合在一起,将上面的平行四边形绕它的一个顶点旋转180°,再通过平移使它与下面的平行四边形重合。观察两个平行四边形的各条边与各个角,你有什么发现?
旋转和平移后的图形,各边与各个角都不变。
发现:平行四边形的对边相等,对角也相等。
三、巩固反馈
判断。
(1)经过一点只能画一条直线。 ( )
(2)大于90°的角是钝角。 ( )
(3)角的边画得越长,角就越大。 ( )
(4)三角形按角分类可以分为钝角三角形、
直角三角形和锐角三角形。 ( )
(5)圆的直径是一条直线。 ( )
(6)两组对边分别平行的四边形一定是平行四边形。 ( )
(7)正方形是特殊的长方形,梯形是特殊的平行四边形。( )
√
×
×
×
×
大于90°而小于180°
角的大小与角的两边的长短无关,与角的张口的大小有关。
梯形不是平行四边形。
圆的直径是一条线段。
√
×
四、课堂小结
通过本节课的复习,你对平面图形又有什么新的体会和收获?
作业:
五、作业布置
1 图形的认识与测量
第1课时 平面图形的认识
——图形与几何
一、回顾整理
图形的分类
封闭图形
不封闭图形
直线、射线、线段、角
图形
长方形
圆
正方形
平行四边形
梯形
三角形
立体图形
平行线、相交线
平面图形
四边形
其余多边形
长方体
圆柱
圆锥
正方体
圆形
扇形
一、回顾整理
直线、射线和线段
射线
线段
直线
区 别
联系
名称
能否延伸
能
不能
不能
能否度量
1个
0个
射线、线段都是直线的一部分
端点个数
2个
可以向两端无限延伸
不能延伸
可以向一端 无限延伸
一、回顾整理
角
{5940675A-B579-460E-94D1-54222C63F5DA}角的
分类
角的范围
图示
锐角
大于0°、小于90°
直角
等于90°
钝角
大于900、小于1800
等于1800
等于3600
周角>平角>钝角>直角>锐角
平角
周角
一、回顾整理
三角形
三角形的分类
三角形按角分
锐角三角形
直角三角形
钝角三角形
(三个角都是锐角)
(有一个角是直角)
(有一个角是钝角)
1
锐角三角形
直角三角形
钝角三角形
三角形按边分
等腰三角形
等腰三角形
不等边三角形
等边三角形
三角形
等腰三角形
等边三角形
(两条边相等)
(三条边都相等)
不等边三角形
(三条边都不相等)
一、回顾整理
三角形
三角形的内角和为180°
一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
三角形的边角关系
2
13cm
4cm
7cm
一、回顾整理
四边形
四边形的分类
四边形
平行四边形
长方形
正方形
梯形
等腰梯形
直角梯形
1
一、回顾整理
四边形
常见的四边形及其特征
{5940675A-B579-460E-94D1-54222C63F5DA}名称
图例
特征
平行四边形
长方形
正方形
梯形
等腰梯形
直角梯形
两腰相等
两组对边分别平行且相等
只有一组对边平行
(1)两组对边分别平行且相等;(2)四个角都是直角
(1)两组对边分别平行;(2)四条边相等;(3)四个角都是直角
有两个角是直角
2
一、回顾整理
圆
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}圆的定义
圆各部分
的名称
圆的特点
圆是一种封闭的曲线图形
(1)圆心:圆中心的一点叫做圆心,如图,点O是圆心。
(2)半径:连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示。
(3)直径:通过圆心且两端都在圆上的线段叫做直径,一般用字母d表示
(1)圆心确定圆的位置,半径决定圆的大小。
(2)同圆或等圆中,半径是直径的一半,直径是半径的2倍。
(3)圆是轴对称图形,圆的直径所在的直线是它的对称轴,它有无数条对称轴
二、知识应用
做两个一样的平行四边形纸片。把它们重合在一起,将上面的平行四边形绕它的一个顶点旋转180°,再通过平移使它与下面的平行四边形重合。观察两个平行四边形的各条边与各个角,你有什么发现?
旋转和平移后的图形,各边与各个角都不变。
发现:平行四边形的对边相等,对角也相等。
三、巩固反馈
判断。
(1)经过一点只能画一条直线。 ( )
(2)大于90°的角是钝角。 ( )
(3)角的边画得越长,角就越大。 ( )
(4)三角形按角分类可以分为钝角三角形、
直角三角形和锐角三角形。 ( )
(5)圆的直径是一条直线。 ( )
(6)两组对边分别平行的四边形一定是平行四边形。 ( )
(7)正方形是特殊的长方形,梯形是特殊的平行四边形。( )
√
×
×
×
×
大于90°而小于180°
角的大小与角的两边的长短无关,与角的张口的大小有关。
梯形不是平行四边形。
圆的直径是一条线段。
√
×
四、课堂小结
通过本节课的复习,你对平面图形又有什么新的体会和收获?
作业:
五、作业布置
