六年级数学下册课件比例理与复习人教版(23张)
文档属性
| 名称 | 六年级数学下册课件比例理与复习人教版(23张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 11:50:27 | ||
图片预览






文档简介
4 整理与复习
比 例
一、回顾整理
什么叫做比例?
表示两个比相等的式子就叫做比例
两个数相除又叫做两个数的比。
什么叫做比?
联系:比是比例的一部分;而比例是由至少两个比值相等的比组合而成的。
比和比例有什么联系和区别?
区别:比表示两个数相除(有两项,前项和后项),比例表示两个比相等的式子(有四项,两个内项,两个外项)。比例是由两个比值相等的比组成的。
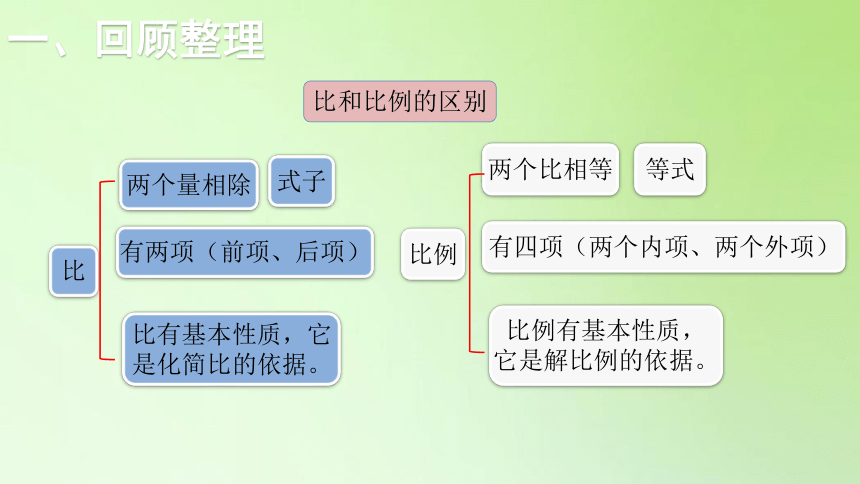
比和比例的区别
比
两个量相除
有两项(前项、后项)
比有基本性质,它是化简比的依据。
比例
等式
两个比相等
式子
有四项(两个内项、两个外项)
比例有基本性质,它是解比例的依据。
一、回顾整理
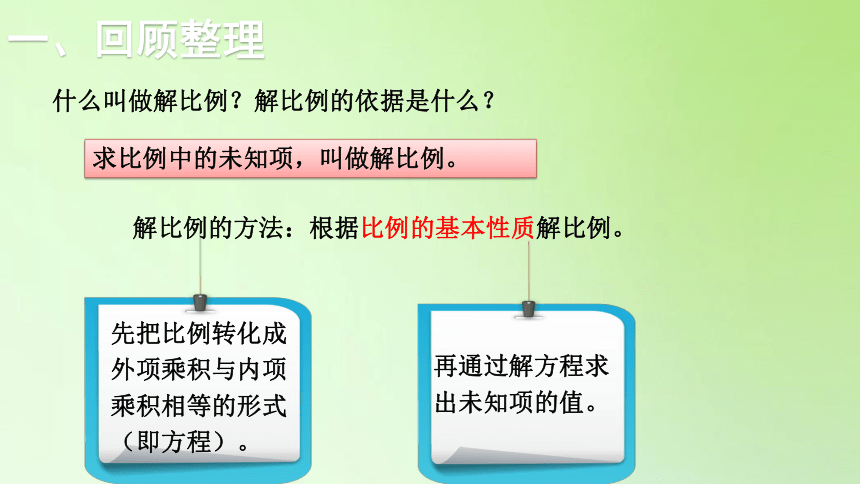
求比例中的未知项,叫做解比例。
先把比例转化成外项乘积与内项乘积相等的形式(即方程)。
解比例的方法:根据比例的基本性质解比例。
再通过解方程求出未知项的值。
一、回顾整理
什么叫做解比例?解比例的依据是什么?
一、回顾整理
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫反比例关系。
什么叫成正比例的量和正比例关系?
什么叫成反比例的量和反比例关系?
{0505E3EF-67EA-436B-97B2-0124C06EBD24}
相同点
不同点
正比例
反比例
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
1.变化的方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)。
2.相关联的两个量相对应的两个数的比值(商)一定。
2.相关联的两个量相对应的两个数的乘积一定
3.关系式:
3.关系式:
正、反比例的联系和区别
yx=
?
k(一定)
xy =k(一定)
都是两种相关联的量,一种量随着另一种量变化。
一、回顾整理
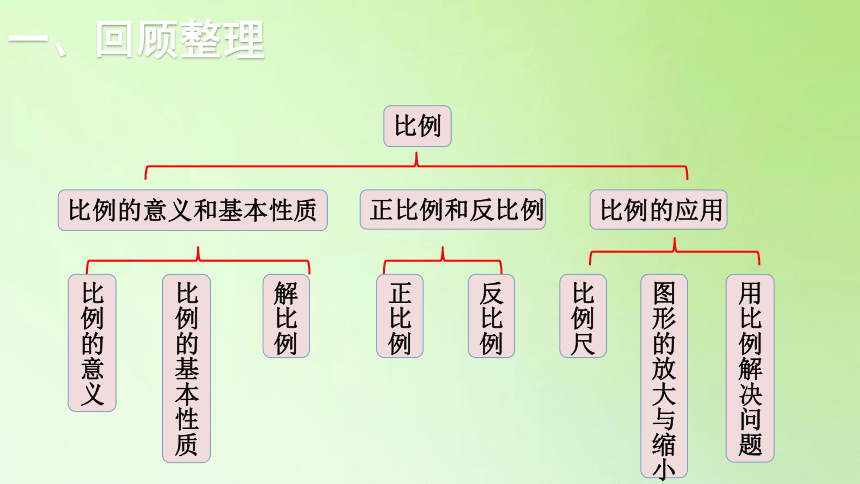
比例
比例的意义和基本性质
比例的应用
比例的意义
比例的基本性质
解比例
比例尺
图形的放大与缩小
正比例和反比例
正比例
反比例
用比例解决问题
一、回顾整理
二、知识应用
2. 解比例的依据是什么?解下面的比例。
x∶ = ∶4
解:5x=4×6
5x=24
x=4.8
解:4x = ×
4x =
x =
整理和复习
二、知识应用
6.5∶x = 3.25∶4
解:3.25x=4×6.5
3.25x=26
x=8
解:1.2x=3×2.5
1.2x=7.5
x=6.25
2. 解比例的依据是什么?解下面的比例。
整理和复习
3.下面每个表中的两个量,哪些成比例关系,成正比例关系还是反比例关系?哪些不成比例关系?
(1)从甲地到乙地的路程是240km,汽车行驶的速度与时间如下表。
{7DF18680-E054-41AD-8BC1-D1AEF772440D}速度/千米/时
40
50
60
80
100
时间/时
6
4.8
4
3
2.4
速度与时间成反比例。
速度ⅹ时间=路程(一定)
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
路程
240
240
240
240
240
二、知识应用
整理和复习
(2)从圆锥的高30cm,它的体积与底面积如下表。
{7DF18680-E054-41AD-8BC1-D1AEF772440D}底面积/cm2
5
8
10
16
20
体积/cm3
50
80
100
160
200
圆锥的体积与底面积成正比例。
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
圆锥的高
30
30
30
30
30
圆锥的体积
底面积
(一定)
圆锥的高
3
=
二、知识应用
3.下面每个表中的两个量,哪些成比例关系,成正比例关系还是反比例关系?哪些不成比例关系?
整理和复习
(3)从圆的半径与圆的面积如下表。
{7DF18680-E054-41AD-8BC1-D1AEF772440D}半径/cm
1
2
3
4
5
面积/cm2
π
4π
9π
16π
25π
圆的半径与面积不成比例。
圆的面积=πⅹ半径2
圆的面积
πⅹ半径
=半径(比值不一定)
二、知识应用
3.下面每个表中的两个量,哪些成比例关系,成正比例关系还是反比例关系?哪些不成比例关系?
整理和复习
二、知识应用
1. 填空。
(1)一幅地图中某两地的图上距离5cm表示实际距离15 km,这幅图的比例尺是( )。
(2)大小两个圆的半径之比是5:3。它们的直径之比( ),周长之比是( ),面积之比是( )。
(3)把一个长5cm、宽3cm的长方形按3:1放大,得到的图形的面积是( )cm?。
1:300000
5:3
25:9
5:3
135
练
习
十
二
4.(1)王叔叔开车从甲地到乙地,前2小时行了100km。照这样的速度,从甲地到乙地一共要用3小时,甲、乙两地相距多远?
解:设甲、乙两地相距x km。
100
2
=
x
3
2x=3×100
x=150
答:甲、乙两地相距150 km。
速度一定
路程与时间成正比例关系
时间
=速度(一定)
路程
二、知识应用
整理和复习
4.(2)王叔叔开车从甲地到乙地一共用了3小时,每小时行50km。原路返回时每小时行60km,返回时用了多长时间?
解:设返回时用了x小时。
x = 2.5
答:返回时用了2.5小时。
路程一定
速度与时间成反比例关系
时间
=路程(一定)
速度×
路程不变。
= 50×3
x
60
x =
60
3×50
二、知识应用
整理和复习
三、巩固反馈
2. 下面各题中的两种量之间是否有比例关系?如果有,成什么
比例关系?
(1)比例尺一定,两地的实际距离和图上距离。
(2)积(O除外)一定,一个因数和另一个因数。
(3)梯形的上底和下底不变,梯形的面积和高。
(4)如果y=5x,y和x。
有比例关系,成正比例关系。
有比例关系,成反比例关系。
有比例关系,成正比例关系。
有比例关系,成正比例关系。
练
习
十
二
3.在一幅比例尺是1∶2000000的地图上,量得甲、乙两个城市之间高速公路的距离是5.5cm。在另一幅比例尺是1∶5000000的地图上,这条公路的图上距离是多少?
1:2000000=5.5:x
x=11000000
11000000×
1
5000000
= 2.2(cm)
答:这条公路的图上距离是2.2 cm。
三、巩固反馈
解:设甲、乙两个城市之间高速公路的实际距离是x km。
练
习
十
二
方法一
先求实际距离,再根据新的比例尺,求出新的图上距离。
5.5×
2
5
=2.2(cm)
答:这条公路的图上距离是2.2 cm。
1
500000
1
200000
÷
=
2
5
三、巩固反馈
新来的比例尺缩小到原来的 ,图上距离也应该是5.5cm的 。
3.在一幅比例尺是1∶2000000的地图上,量得甲、乙两个城市之间高速公路的距离是5.5cm。在另一幅比例尺是1∶5000000的地图上,这条公路的图上距离是多少?
练
习
十
二
方法二
4.一个服装店的所有衣服都打同样的折扣销售。
(1)李阿姨买了一件上衣,原价250元,现价150元。李阿姨还想买一条裤子,原价180元,现价多少元钱?
解:设现价是x元。
250
150
=
180
x
250x=150×180
x=108
答:现价108元。
折扣相同,现价与原价成正比例。
三、巩固反馈
上衣原价和现价比值
裤子原价和现价比值
练
习
十
二
(2)张伯伯有一笔钱,如果买现价90元一件的衬衫,正好买4件。如果想买原价200元一件的夹克衫,能买多少件?
解:设一件夹克衫的现价是x元,能买y件。
答:一件夹克衫的现价是120元,能买3件。
总钱数相同,数量与单价成反比例。
三、巩固反馈
250
150
=
180
x
x = 120
120y=90×4
y=3
4.一个服装店的所有衣服都打同样的折扣销售。
练
习
十
二
(3)如果用x表示原价,y表示现价,y和x的关系式为__________。
现价:原价=
现价
原价
=折扣
150
250
三、巩固反馈
=
3
5
4.一个服装店的所有衣服都打同样的折扣销售。
练
习
十
二
1.比和比例的联系:比是比例的一部分;而比例是由至少两个比值相等的比组合而成的。
2.解比例时要先把比例转化成外项乘积与内项乘积相等的形式(即方程)。再通过解方程求出未知项的值。
3.正比例和反比例都是两种相关联的量,一种量随着另一种量变化。
4.反比例关系式: 正比例关系式:
四、课堂小结
xy =k(一定)
yx=
?
k(一定)
作业:
五、作业布置
比 例
一、回顾整理
什么叫做比例?
表示两个比相等的式子就叫做比例
两个数相除又叫做两个数的比。
什么叫做比?
联系:比是比例的一部分;而比例是由至少两个比值相等的比组合而成的。
比和比例有什么联系和区别?
区别:比表示两个数相除(有两项,前项和后项),比例表示两个比相等的式子(有四项,两个内项,两个外项)。比例是由两个比值相等的比组成的。
比和比例的区别
比
两个量相除
有两项(前项、后项)
比有基本性质,它是化简比的依据。
比例
等式
两个比相等
式子
有四项(两个内项、两个外项)
比例有基本性质,它是解比例的依据。
一、回顾整理
求比例中的未知项,叫做解比例。
先把比例转化成外项乘积与内项乘积相等的形式(即方程)。
解比例的方法:根据比例的基本性质解比例。
再通过解方程求出未知项的值。
一、回顾整理
什么叫做解比例?解比例的依据是什么?
一、回顾整理
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫反比例关系。
什么叫成正比例的量和正比例关系?
什么叫成反比例的量和反比例关系?
{0505E3EF-67EA-436B-97B2-0124C06EBD24}
相同点
不同点
正比例
反比例
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
1.变化的方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)。
2.相关联的两个量相对应的两个数的比值(商)一定。
2.相关联的两个量相对应的两个数的乘积一定
3.关系式:
3.关系式:
正、反比例的联系和区别
yx=
?
k(一定)
xy =k(一定)
都是两种相关联的量,一种量随着另一种量变化。
一、回顾整理
比例
比例的意义和基本性质
比例的应用
比例的意义
比例的基本性质
解比例
比例尺
图形的放大与缩小
正比例和反比例
正比例
反比例
用比例解决问题
一、回顾整理
二、知识应用
2. 解比例的依据是什么?解下面的比例。
x∶ = ∶4
解:5x=4×6
5x=24
x=4.8
解:4x = ×
4x =
x =
整理和复习
二、知识应用
6.5∶x = 3.25∶4
解:3.25x=4×6.5
3.25x=26
x=8
解:1.2x=3×2.5
1.2x=7.5
x=6.25
2. 解比例的依据是什么?解下面的比例。
整理和复习
3.下面每个表中的两个量,哪些成比例关系,成正比例关系还是反比例关系?哪些不成比例关系?
(1)从甲地到乙地的路程是240km,汽车行驶的速度与时间如下表。
{7DF18680-E054-41AD-8BC1-D1AEF772440D}速度/千米/时
40
50
60
80
100
时间/时
6
4.8
4
3
2.4
速度与时间成反比例。
速度ⅹ时间=路程(一定)
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
路程
240
240
240
240
240
二、知识应用
整理和复习
(2)从圆锥的高30cm,它的体积与底面积如下表。
{7DF18680-E054-41AD-8BC1-D1AEF772440D}底面积/cm2
5
8
10
16
20
体积/cm3
50
80
100
160
200
圆锥的体积与底面积成正比例。
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
圆锥的高
30
30
30
30
30
圆锥的体积
底面积
(一定)
圆锥的高
3
=
二、知识应用
3.下面每个表中的两个量,哪些成比例关系,成正比例关系还是反比例关系?哪些不成比例关系?
整理和复习
(3)从圆的半径与圆的面积如下表。
{7DF18680-E054-41AD-8BC1-D1AEF772440D}半径/cm
1
2
3
4
5
面积/cm2
π
4π
9π
16π
25π
圆的半径与面积不成比例。
圆的面积=πⅹ半径2
圆的面积
πⅹ半径
=半径(比值不一定)
二、知识应用
3.下面每个表中的两个量,哪些成比例关系,成正比例关系还是反比例关系?哪些不成比例关系?
整理和复习
二、知识应用
1. 填空。
(1)一幅地图中某两地的图上距离5cm表示实际距离15 km,这幅图的比例尺是( )。
(2)大小两个圆的半径之比是5:3。它们的直径之比( ),周长之比是( ),面积之比是( )。
(3)把一个长5cm、宽3cm的长方形按3:1放大,得到的图形的面积是( )cm?。
1:300000
5:3
25:9
5:3
135
练
习
十
二
4.(1)王叔叔开车从甲地到乙地,前2小时行了100km。照这样的速度,从甲地到乙地一共要用3小时,甲、乙两地相距多远?
解:设甲、乙两地相距x km。
100
2
=
x
3
2x=3×100
x=150
答:甲、乙两地相距150 km。
速度一定
路程与时间成正比例关系
时间
=速度(一定)
路程
二、知识应用
整理和复习
4.(2)王叔叔开车从甲地到乙地一共用了3小时,每小时行50km。原路返回时每小时行60km,返回时用了多长时间?
解:设返回时用了x小时。
x = 2.5
答:返回时用了2.5小时。
路程一定
速度与时间成反比例关系
时间
=路程(一定)
速度×
路程不变。
= 50×3
x
60
x =
60
3×50
二、知识应用
整理和复习
三、巩固反馈
2. 下面各题中的两种量之间是否有比例关系?如果有,成什么
比例关系?
(1)比例尺一定,两地的实际距离和图上距离。
(2)积(O除外)一定,一个因数和另一个因数。
(3)梯形的上底和下底不变,梯形的面积和高。
(4)如果y=5x,y和x。
有比例关系,成正比例关系。
有比例关系,成反比例关系。
有比例关系,成正比例关系。
有比例关系,成正比例关系。
练
习
十
二
3.在一幅比例尺是1∶2000000的地图上,量得甲、乙两个城市之间高速公路的距离是5.5cm。在另一幅比例尺是1∶5000000的地图上,这条公路的图上距离是多少?
1:2000000=5.5:x
x=11000000
11000000×
1
5000000
= 2.2(cm)
答:这条公路的图上距离是2.2 cm。
三、巩固反馈
解:设甲、乙两个城市之间高速公路的实际距离是x km。
练
习
十
二
方法一
先求实际距离,再根据新的比例尺,求出新的图上距离。
5.5×
2
5
=2.2(cm)
答:这条公路的图上距离是2.2 cm。
1
500000
1
200000
÷
=
2
5
三、巩固反馈
新来的比例尺缩小到原来的 ,图上距离也应该是5.5cm的 。
3.在一幅比例尺是1∶2000000的地图上,量得甲、乙两个城市之间高速公路的距离是5.5cm。在另一幅比例尺是1∶5000000的地图上,这条公路的图上距离是多少?
练
习
十
二
方法二
4.一个服装店的所有衣服都打同样的折扣销售。
(1)李阿姨买了一件上衣,原价250元,现价150元。李阿姨还想买一条裤子,原价180元,现价多少元钱?
解:设现价是x元。
250
150
=
180
x
250x=150×180
x=108
答:现价108元。
折扣相同,现价与原价成正比例。
三、巩固反馈
上衣原价和现价比值
裤子原价和现价比值
练
习
十
二
(2)张伯伯有一笔钱,如果买现价90元一件的衬衫,正好买4件。如果想买原价200元一件的夹克衫,能买多少件?
解:设一件夹克衫的现价是x元,能买y件。
答:一件夹克衫的现价是120元,能买3件。
总钱数相同,数量与单价成反比例。
三、巩固反馈
250
150
=
180
x
x = 120
120y=90×4
y=3
4.一个服装店的所有衣服都打同样的折扣销售。
练
习
十
二
(3)如果用x表示原价,y表示现价,y和x的关系式为__________。
现价:原价=
现价
原价
=折扣
150
250
三、巩固反馈
=
3
5
4.一个服装店的所有衣服都打同样的折扣销售。
练
习
十
二
1.比和比例的联系:比是比例的一部分;而比例是由至少两个比值相等的比组合而成的。
2.解比例时要先把比例转化成外项乘积与内项乘积相等的形式(即方程)。再通过解方程求出未知项的值。
3.正比例和反比例都是两种相关联的量,一种量随着另一种量变化。
4.反比例关系式: 正比例关系式:
四、课堂小结
xy =k(一定)
yx=
?
k(一定)
作业:
五、作业布置
