六年级数学下册课件比例的应用练习课人教版(19张)
文档属性
| 名称 | 六年级数学下册课件比例的应用练习课人教版(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 11:56:23 | ||
图片预览




文档简介
3 比例的应用
第6课时 练习课
比 例
一、复习回顾
你能说一说图形放大或缩小后的特点吗?
放大后的图形边长变大了,周长变大了,内角的度数没有改变。放大后的图形与原图形相比,形状没有变,图形变大了。
缩小后的图形边长变小了,周长变小了,内角的度数没有改变。缩小后的图形与原图形相比,形状没有变,图形变小了。
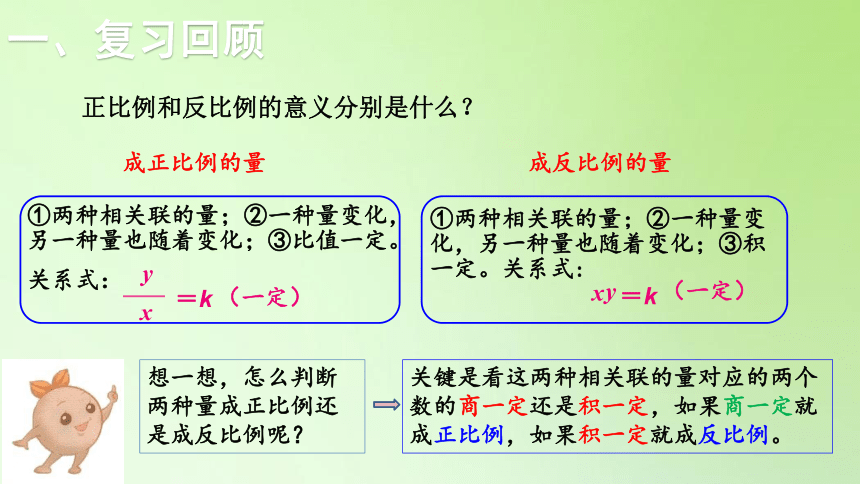
成正比例的量
①两种相关联的量;②一种量变化,另一种量也随着变化;③积一定。关系式:
y
x
=k
(一定)
关键是看这两种相关联的量对应的两个数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例。
想一想,怎么判断两种量成正比例还是成反比例呢?
成反比例的量
①两种相关联的量;②一种量变化,另一种量也随着变化;③比值一定。
关系式:
y
x
=k
(一定)
一、复习回顾
正比例和反比例的意义分别是什么?
一、复习回顾
正比例和反比例的意义分别是什么?
成正比例的量一种量扩大,另一种量也扩大;一种量缩小,另一种量也缩小。
成反比例的量一种量扩大,另一种量就缩小;一种量扩大,另一种量也缩小。
二、指导练习
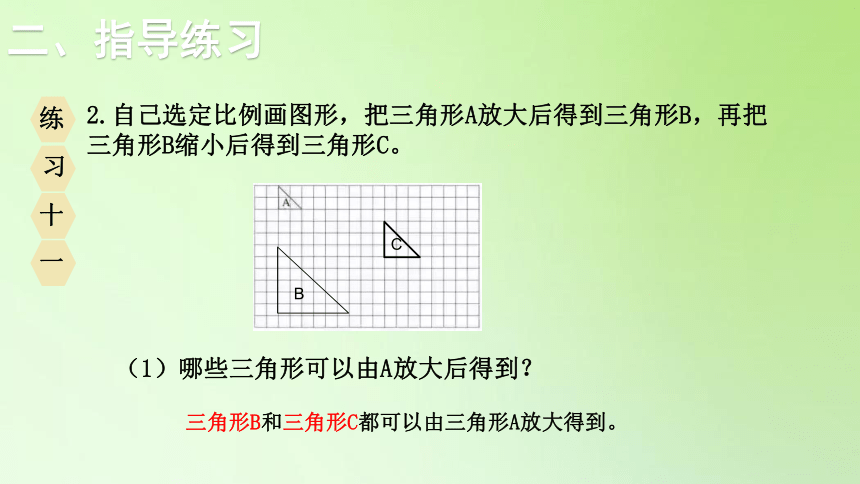
2.自己选定比例画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
B
C
(1)哪些三角形可以由A放大后得到?
三角形B和三角形C都可以由三角形A放大得到。
练
习
十
一
二、指导练习
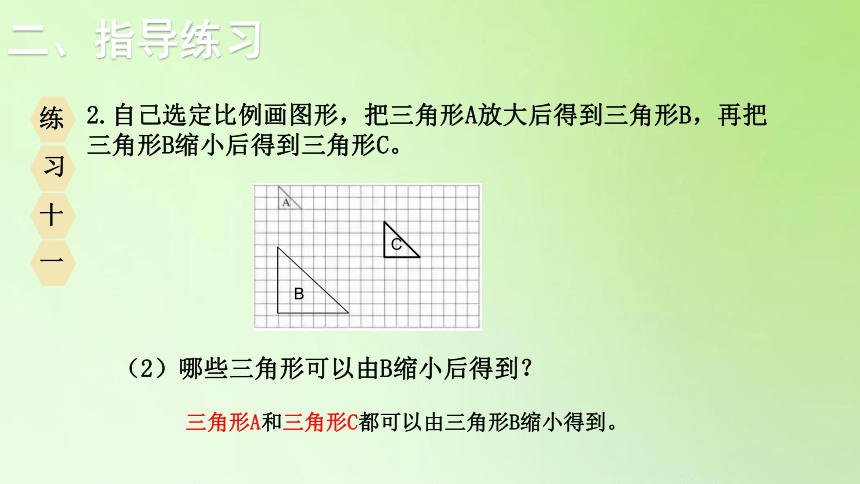
2.自己选定比例画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
B
C
(2)哪些三角形可以由B缩小后得到?
三角形A和三角形C都可以由三角形B缩小得到。
练
习
十
一
二、指导练习
2.自己选定比例画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
B
C
(3)观察三角形A和B,它们的面积有什么变化?面积和边长是按相同的比变化的吗?
三角形B的面积:6×6÷2=18。
三角形A的面积:2×2÷2=2。
三角形A的边长:三角形B的边长=2:6=1:3
三角形A的面积:三角形B的面积=2:18=1:9
面积比和边长比不相同
练
习
十
一
3.小兰的身高1.5m,她的影长是2.4m,如果同一时间、同一地点测得一棵树的影子长4m,这棵树有多高?
解:设这棵树高x m。
????.????????.????=????????
?
2.4x=4×1.5
x=2.5
答:这棵树高2.5m。
小兰的影长
小兰的身高
树的影长
树的身高
二、指导练习
练
习
十
一
4.我国发射的人造地球卫星在空中绕地球运行6周需要10.6小时,运行15周要用多少时间?
解:设运行15周要用x小时。
10.6∶6=x∶15
x=26.5
答:运行15周要用26.5小时。
二、指导练习
练
习
十
一
5.工程队修一条水渠,每天工作6小时,12天可以完成任务。如果工作效率不变,每天工作8小时,多少天可以完成任务?
解:设x天可以完成任务。
8x=6×12
x=9
答:9天可以完成任务。
修完水渠所需的总小时数不变,每天工作小时数×工作天数=总小时数。
二、指导练习
练
习
十
一
8.小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?
解:设平均每天要读x页。
6x=30×8
x=40
答:平均每天要读40页。
总页数不变,每天读的页数和天数成反比例关系。
二、指导练习
练
习
十
一
三、巩固练习
6.北京到长沙的铁路长大约是1600km。一列由北京开往长沙的高铁,9:00出发,11:30到达郑州。北京到郑州的铁路长大约是700km。按照这样的平均速度,从北京到长沙6小时能到吗?
解:设从北京到长沙需要x小时。
11:30-9:00=2小时30分=2.5小时
从北京到长沙6小时能到。
练
习
十
一
三、巩固练习
7.一列货车前往灾区运送救灾物资处,2小时行驶了30km。从出发地点到灾区有90km,按照这样的速度,全程需要多少小时?
解:设全程需要x小时。
30x=2×90
x=6
答:全程需要6个小时。
练
习
十
一
9.小明家用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
解:设每小时应收割x公顷。
30x=0.3×40
x=0.4
(1)现在想用30小时收割完,那么每小时应收割多少公顷?
x=????.????×????????????????
?
答:每小时应收割0.4公顷。
工作总量一定,工作时间和工作效率成反比例关系。
三、巩固练习
练
习
十
一
0.3×40×8
=12×8
答:这块地共产小麦96 t。
=96(t)
(2)每公顷产小麦8t,这块地共产小麦多少吨?
先求出小麦的公顷数。
三、巩固练习
9.小明家用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
练
习
十
一
三、巩固练习
(3)你能提出其他数学问题并解答吗?
如提问:
如果每小时收割0.8公顷,那么需要多少小时才能收割完?
解:设需要x小时才能收割完。
0.3×40=0.8x
x=15
答:需要15小时才能收割完。
9.小明家用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
练
习
十
一
10.一辆汽车从甲地到乙地,平均每小时行72km,10小时到达。回来时空车原路返回,每小时可行90km,多长时间能够返回原地?
解:设x小时能够返回原地。
90x = 72×10
x=8
答:8小时能够返回原地。
回来时的路程
去时的路程
三、巩固练习
练
习
十
一
1.根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项,这个过程叫做解比例。
2.在解答题中,我们可以用解比例来求出题中的未知量。
四、课堂小结
作业:
五、作业布置
第6课时 练习课
比 例
一、复习回顾
你能说一说图形放大或缩小后的特点吗?
放大后的图形边长变大了,周长变大了,内角的度数没有改变。放大后的图形与原图形相比,形状没有变,图形变大了。
缩小后的图形边长变小了,周长变小了,内角的度数没有改变。缩小后的图形与原图形相比,形状没有变,图形变小了。
成正比例的量
①两种相关联的量;②一种量变化,另一种量也随着变化;③积一定。关系式:
y
x
=k
(一定)
关键是看这两种相关联的量对应的两个数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例。
想一想,怎么判断两种量成正比例还是成反比例呢?
成反比例的量
①两种相关联的量;②一种量变化,另一种量也随着变化;③比值一定。
关系式:
y
x
=k
(一定)
一、复习回顾
正比例和反比例的意义分别是什么?
一、复习回顾
正比例和反比例的意义分别是什么?
成正比例的量一种量扩大,另一种量也扩大;一种量缩小,另一种量也缩小。
成反比例的量一种量扩大,另一种量就缩小;一种量扩大,另一种量也缩小。
二、指导练习
2.自己选定比例画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
B
C
(1)哪些三角形可以由A放大后得到?
三角形B和三角形C都可以由三角形A放大得到。
练
习
十
一
二、指导练习
2.自己选定比例画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
B
C
(2)哪些三角形可以由B缩小后得到?
三角形A和三角形C都可以由三角形B缩小得到。
练
习
十
一
二、指导练习
2.自己选定比例画图形,把三角形A放大后得到三角形B,再把三角形B缩小后得到三角形C。
B
C
(3)观察三角形A和B,它们的面积有什么变化?面积和边长是按相同的比变化的吗?
三角形B的面积:6×6÷2=18。
三角形A的面积:2×2÷2=2。
三角形A的边长:三角形B的边长=2:6=1:3
三角形A的面积:三角形B的面积=2:18=1:9
面积比和边长比不相同
练
习
十
一
3.小兰的身高1.5m,她的影长是2.4m,如果同一时间、同一地点测得一棵树的影子长4m,这棵树有多高?
解:设这棵树高x m。
????.????????.????=????????
?
2.4x=4×1.5
x=2.5
答:这棵树高2.5m。
小兰的影长
小兰的身高
树的影长
树的身高
二、指导练习
练
习
十
一
4.我国发射的人造地球卫星在空中绕地球运行6周需要10.6小时,运行15周要用多少时间?
解:设运行15周要用x小时。
10.6∶6=x∶15
x=26.5
答:运行15周要用26.5小时。
二、指导练习
练
习
十
一
5.工程队修一条水渠,每天工作6小时,12天可以完成任务。如果工作效率不变,每天工作8小时,多少天可以完成任务?
解:设x天可以完成任务。
8x=6×12
x=9
答:9天可以完成任务。
修完水渠所需的总小时数不变,每天工作小时数×工作天数=总小时数。
二、指导练习
练
习
十
一
8.小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?
解:设平均每天要读x页。
6x=30×8
x=40
答:平均每天要读40页。
总页数不变,每天读的页数和天数成反比例关系。
二、指导练习
练
习
十
一
三、巩固练习
6.北京到长沙的铁路长大约是1600km。一列由北京开往长沙的高铁,9:00出发,11:30到达郑州。北京到郑州的铁路长大约是700km。按照这样的平均速度,从北京到长沙6小时能到吗?
解:设从北京到长沙需要x小时。
11:30-9:00=2小时30分=2.5小时
从北京到长沙6小时能到。
练
习
十
一
三、巩固练习
7.一列货车前往灾区运送救灾物资处,2小时行驶了30km。从出发地点到灾区有90km,按照这样的速度,全程需要多少小时?
解:设全程需要x小时。
30x=2×90
x=6
答:全程需要6个小时。
练
习
十
一
9.小明家用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
解:设每小时应收割x公顷。
30x=0.3×40
x=0.4
(1)现在想用30小时收割完,那么每小时应收割多少公顷?
x=????.????×????????????????
?
答:每小时应收割0.4公顷。
工作总量一定,工作时间和工作效率成反比例关系。
三、巩固练习
练
习
十
一
0.3×40×8
=12×8
答:这块地共产小麦96 t。
=96(t)
(2)每公顷产小麦8t,这块地共产小麦多少吨?
先求出小麦的公顷数。
三、巩固练习
9.小明家用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
练
习
十
一
三、巩固练习
(3)你能提出其他数学问题并解答吗?
如提问:
如果每小时收割0.8公顷,那么需要多少小时才能收割完?
解:设需要x小时才能收割完。
0.3×40=0.8x
x=15
答:需要15小时才能收割完。
9.小明家用收割机收割小麦。如果每小时收割0.3公顷,40小时能完成任务。
练
习
十
一
10.一辆汽车从甲地到乙地,平均每小时行72km,10小时到达。回来时空车原路返回,每小时可行90km,多长时间能够返回原地?
解:设x小时能够返回原地。
90x = 72×10
x=8
答:8小时能够返回原地。
回来时的路程
去时的路程
三、巩固练习
练
习
十
一
1.根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项,这个过程叫做解比例。
2.在解答题中,我们可以用解比例来求出题中的未知量。
四、课堂小结
作业:
五、作业布置
