六年级数学下册课件-4.3 第1课时 比例尺-人教版(共17张PPT)
文档属性
| 名称 | 六年级数学下册课件-4.3 第1课时 比例尺-人教版(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-06 00:00:00 | ||
图片预览



文档简介
3 比例的应用
第1课时 比例尺
比 例
一、情境引入
二、学习新课
如果要把一条2m长的线段画在作业本上,你准备用图上几厘米表示实际2m?试着画一画。
区分一下我们在作业本上画的2m与生活中的2m有什么区别?
图上距离
实际距离
二、学习新课
比例尺
图上距离是比的前项;
实际距离是比的后项。
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
二、学习新课
比例尺
图上距离︰实际距离=比例尺
或
图上距离
实际距离
=
比例尺
二、学习新课
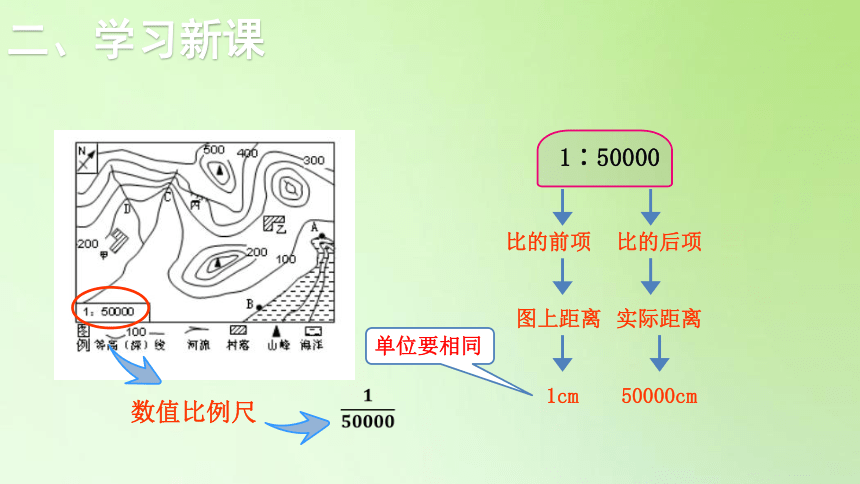
数值比例尺
1∶50000
比的前项
比的后项
图上距离
实际距离
1cm
50000cm
?
单位要相同
二、学习新课
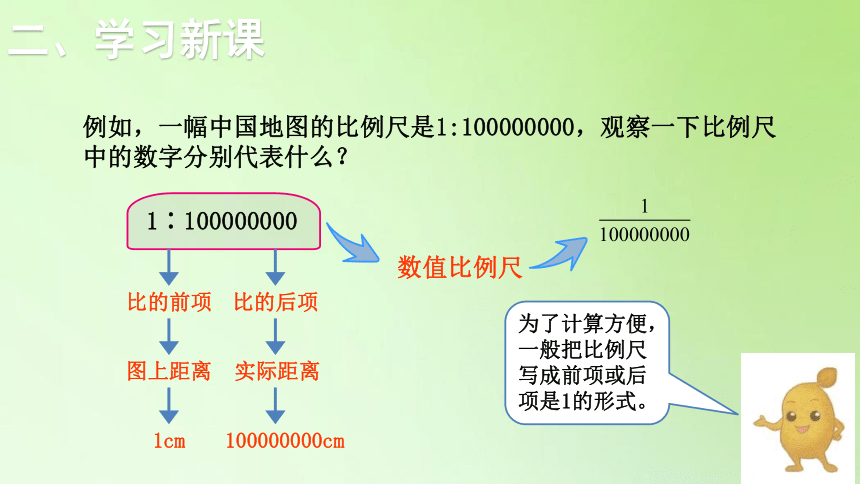
例如,一幅中国地图的比例尺是1:100000000,观察一下比例尺中的数字分别代表什么?
1∶100000000
比的前项
比的后项
图上距离
实际距离
1cm
100000000cm
数值比例尺
为了计算方便,一般把比例尺写成前项或后项是1的形式。
二、学习新课
线段比例尺
地图上1cm的距离相当于地面上50km的实际距离。
把线段比例尺改成数值比例尺。
图上距离∶实际距离
=1 cm∶50 km
=1 cm∶5000000 cm
=1∶5000000
二、学习新课
在绘制比较精细的零件图时,经常需要把零件的尺寸按一定的比放大,如一幅零件图纸的比例尺2∶1,你知道它表示什么吗?
?
二、学习新课
缩小比例尺:在绘图时,有时需要把实际距离按一定的比例缩小后在图纸上画出来,用这种方法得到的比例尺就是缩小比例尺。前面提到的比例尺1:100000000,比例尺1:5000000都是缩小比例尺。为了计算方便,把缩小比例尺写成带比号的形式,前项一般化为1;若写成分数形式,分子一般化为1。
观察前面的几个比例尺,发现它们有什么区别?
分为缩小比例尺和放大比例尺两种
二、学习新课
放大比例尺:在绘制比较精细的零件图时,经常需要把零件的尺寸按一定的比放大后画在图纸上,这样的比例尺就是放大比例尺。如一幅零件图纸的比例尺是2:1,它表示图上距离2cm 相当于实际距离1cm,就是图上距离是实际距离的2倍,这是一个放大比例尺。为了计算方便,通常把放大比例尺的后项写成1。
北京到天津的实际距离是120km,在一幅地图上量得两地的图上距离是2.4cm。这幅地图的比例尺是多少?
图上距离∶实际距离=比例尺
120km = 12000000cm
2.4∶12000000 = 1∶5000000
答:这幅图的比例尺是1∶5000000。
二、学习新课
一个圆柱形的零件的高是5mm,在图纸上高是2cm。这幅图纸的比例尺是多少?
三、巩固反馈
图上距离:实际距离=比例尺
2cm=20mm
20∶5=4∶1
答:这幅图纸的比例尺是4∶1。
比的后项是1,放大比例尺。
三、巩固反馈
1. 一幅地图的比例尺是1∶30000000,你能用线段比例尺表示出来吗?
图上1cm相当于实际30000000cm。
线段比例尺在实际中一般用300km更简洁。
30000000cm=300km
0
300km
练
习
十
三、巩固反馈
1.把
2.在一幅地图上量得甲、乙两地的距离是4 cm,而甲、乙两地的实际距离是180 km,这幅地图的比例尺是多少?
改写成数值比例尺是( )
A.1:4000000
B.1:8000000
C.1:12000000
180 km=18000000 cm
4:18000000=1:4500000
A
1.一幅图的图上距离和实际距离的比,叫做这幅图的比例尺;
2.图上距离是比的前项;实际距离是比的后项;
3.在计算比例尺时,数值的单位要统一。
四、课堂小结
作业:
五、作业布置
第1课时 比例尺
比 例
一、情境引入
二、学习新课
如果要把一条2m长的线段画在作业本上,你准备用图上几厘米表示实际2m?试着画一画。
区分一下我们在作业本上画的2m与生活中的2m有什么区别?
图上距离
实际距离
二、学习新课
比例尺
图上距离是比的前项;
实际距离是比的后项。
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
二、学习新课
比例尺
图上距离︰实际距离=比例尺
或
图上距离
实际距离
=
比例尺
二、学习新课
数值比例尺
1∶50000
比的前项
比的后项
图上距离
实际距离
1cm
50000cm
?
单位要相同
二、学习新课
例如,一幅中国地图的比例尺是1:100000000,观察一下比例尺中的数字分别代表什么?
1∶100000000
比的前项
比的后项
图上距离
实际距离
1cm
100000000cm
数值比例尺
为了计算方便,一般把比例尺写成前项或后项是1的形式。
二、学习新课
线段比例尺
地图上1cm的距离相当于地面上50km的实际距离。
把线段比例尺改成数值比例尺。
图上距离∶实际距离
=1 cm∶50 km
=1 cm∶5000000 cm
=1∶5000000
二、学习新课
在绘制比较精细的零件图时,经常需要把零件的尺寸按一定的比放大,如一幅零件图纸的比例尺2∶1,你知道它表示什么吗?
?
二、学习新课
缩小比例尺:在绘图时,有时需要把实际距离按一定的比例缩小后在图纸上画出来,用这种方法得到的比例尺就是缩小比例尺。前面提到的比例尺1:100000000,比例尺1:5000000都是缩小比例尺。为了计算方便,把缩小比例尺写成带比号的形式,前项一般化为1;若写成分数形式,分子一般化为1。
观察前面的几个比例尺,发现它们有什么区别?
分为缩小比例尺和放大比例尺两种
二、学习新课
放大比例尺:在绘制比较精细的零件图时,经常需要把零件的尺寸按一定的比放大后画在图纸上,这样的比例尺就是放大比例尺。如一幅零件图纸的比例尺是2:1,它表示图上距离2cm 相当于实际距离1cm,就是图上距离是实际距离的2倍,这是一个放大比例尺。为了计算方便,通常把放大比例尺的后项写成1。
北京到天津的实际距离是120km,在一幅地图上量得两地的图上距离是2.4cm。这幅地图的比例尺是多少?
图上距离∶实际距离=比例尺
120km = 12000000cm
2.4∶12000000 = 1∶5000000
答:这幅图的比例尺是1∶5000000。
二、学习新课
一个圆柱形的零件的高是5mm,在图纸上高是2cm。这幅图纸的比例尺是多少?
三、巩固反馈
图上距离:实际距离=比例尺
2cm=20mm
20∶5=4∶1
答:这幅图纸的比例尺是4∶1。
比的后项是1,放大比例尺。
三、巩固反馈
1. 一幅地图的比例尺是1∶30000000,你能用线段比例尺表示出来吗?
图上1cm相当于实际30000000cm。
线段比例尺在实际中一般用300km更简洁。
30000000cm=300km
0
300km
练
习
十
三、巩固反馈
1.把
2.在一幅地图上量得甲、乙两地的距离是4 cm,而甲、乙两地的实际距离是180 km,这幅地图的比例尺是多少?
改写成数值比例尺是( )
A.1:4000000
B.1:8000000
C.1:12000000
180 km=18000000 cm
4:18000000=1:4500000
A
1.一幅图的图上距离和实际距离的比,叫做这幅图的比例尺;
2.图上距离是比的前项;实际距离是比的后项;
3.在计算比例尺时,数值的单位要统一。
四、课堂小结
作业:
五、作业布置
