六年级数学下册课件比例的意义和基本性质练习课人教版(19张)
文档属性
| 名称 | 六年级数学下册课件比例的意义和基本性质练习课人教版(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 13:26:38 | ||
图片预览




文档简介
1 比例的意义和基本性质
第4课时 练习课
比 例
表示两个比相等的式子叫做比例。
15∶9 =
20∶12
两个比用等于号连接。
2.4
1.6
60
40
=
分数形式的比
用字母表示:
a∶b=c∶d(b,d≠0)
=
或
b
a
d
c
一、复习回顾
什么是比例?
求比例中的未知项,叫做解比例。
先把比例转化成外项乘积与内项乘积相等的形式(即方程)。
解比例的方法:根据比例的基本性质解比例。
再通过解方程求出未知项的值。
一、复习回顾
什么叫做解比例?解比例的依据是什么?
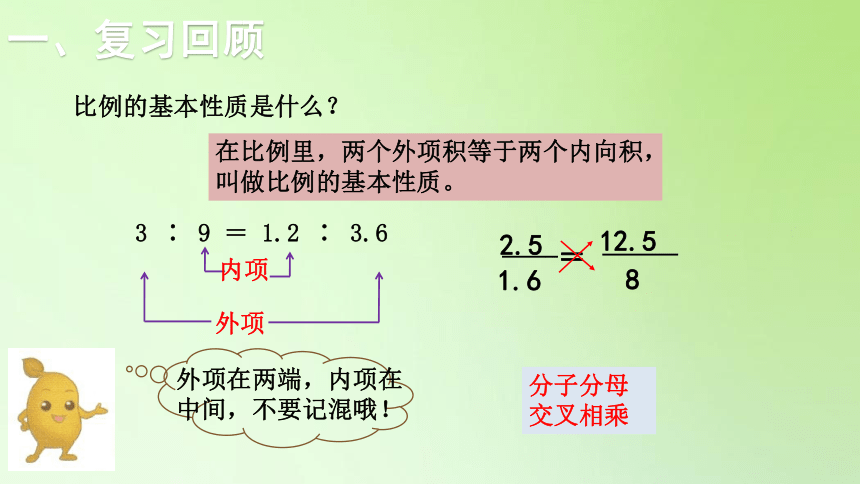
在比例里,两个外项积等于两个内向积,叫做比例的基本性质。
内项
外项
3 ∶ 9 = 1.2 ∶ 3.6
外项在两端,内项在中间,不要记混哦!
=
1.6
2.5
8
12.5
分子分母交叉相乘
一、复习回顾
比例的基本性质是什么?
二、指导练习
2.哪组中的四个数可以组成比例?把组成的比例写出来。
(1)4,5,12和15
(2)2,3,4和5
4×15=60
5×12=60
可以组成比例
4:5=12:15
2×5=10
3×4=12
不可以组成比例
练
习
八
二、指导练习
(3)1.6,6.4,2和5
(4) 和
1.6×6.4=10.24
5×2=10
不可以组成比例
可以组成比例
2.哪组中的四个数可以组成比例?把组成的比例写出来。
练
习
八
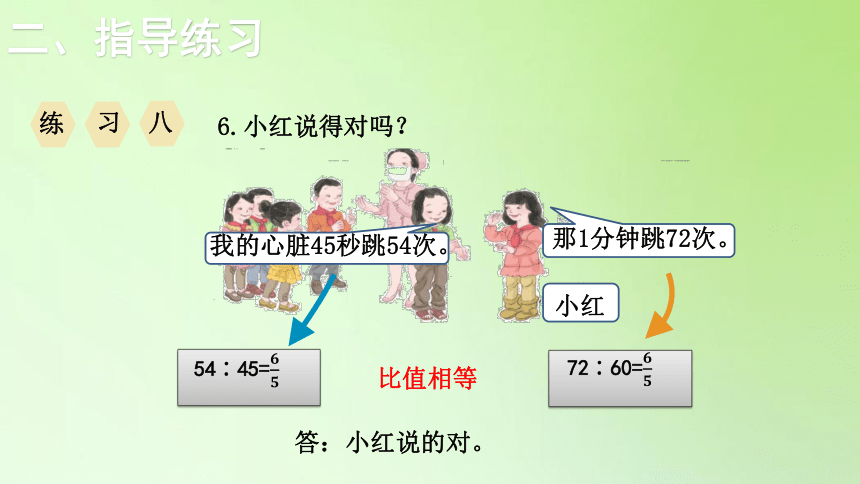
6.小红说得对吗?
那1分钟跳72次。
我的心脏45秒跳54次。
小红
54∶45=????????
?
72∶60=????????
?
答:小红说的对。
比值相等
二、指导练习
练
习
八
7.已知24×3=8×9,根据比例的基本性质,把等式改写比例。
8∶24=3∶9
9∶24=3∶8
8∶3=24∶9
9∶3=24∶8
24∶8=9∶3
24∶9=8∶3
3∶8=9∶24
3∶9=8∶24
24和3作外项,8和9作内项
8和9作外项,24和3作内项
二、指导练习
练
习
八
二、指导练习
8.解比例。
(1)
(2)0.8:4=x:8
解:
解:4x=0.8×8
4x=6.4
x=1.6
练
习
八
二、指导练习
(3)
(4)
解:3x=12×
3x=9
x=3
解:2x=9×8
2x=72
x=36
8.解比例。
练
习
八
11.汽车厂按1∶20的比例生产了一批汽车模型。
(1)轿车模型长24.3 cm,轿车的实际长度是多少?
解:设轿车的实际长度是x cm。
24.3∶x=1∶20
x=486
486 cm=4.86 m
答:轿车的实际长度是4.86 m。
两个比所对应的前后项的量是一致的哦!
二、指导练习
练
习
八
(2)公共汽车长11.76 cm,模型车的长度是多少?
解:设模型车的长度是y m。
y∶11.76=1∶20
y=0.588
0.588 m=58.8 cm
答:模型车的长度是58.8 cm。
二、指导练习
11.汽车厂按1∶20的比例生产了一批汽车模型。
练
习
八
12.博物馆展出了一个高为19.6cm的秦代将军俑模型,它的高度与实际高度的比是1∶10。这个将军俑的实际高度是多少?
解:设将军俑的实际高度是x cm。
19.6∶x=1∶10
x=196
答:将军俑的实际高度是196 cm。
三、巩固练习
练
习
八
三、巩固练习
13.育新小区1号楼的实际高度为35 m,它的高度与模型高度的比是500:1。模型的高度是多少厘米?
解:设模型的高度是x cm。
3500:x=500:1
35 m=3500 cm
500x=3500
x=7
答:模型的高度是7 cm。
练
习
八
14.把下列等式改写成比例。
(1)3×40=8×15
(2)2.5×0.4=0.5×2
3:8=15:40
3:15=8:40
8:3=40:15
15:3=40:8
2.5:0.5=2:0.4
2.5:2=0.5:0.4
0.5:2.5=0.4:2
2:2.5=0.4:0.5
三、巩固练习
练
习
八
……
……
15.李老师买了6个足球和8个篮球,买两种球所花钱数相等。
(1)足球与篮球的单价之比是多少?
三、巩固练习
足球的单价:篮球的单价=8:6
足球的单价:篮球的单价=8:6=4:3
足球的单价×数量=篮球的单价×数量
练
习
八
(2)足球的单价是40元,篮球的单价是多少?
40∶ x=8∶6
解:设篮球的单价是x元。
8x=40×6
x=30
答:篮球的单价是30元。
三、巩固练习
练
习
八
15.李老师买了6个足球和8个篮球,买两种球所花钱数相等。
1.表示两个比相等的式子叫做比例。
2.求比例中的未知项,叫做解比例。
3.在比例里,两个外项的积等于两个内项的积,
这叫做比例的基本性质。
四、课堂小结
作业:
五、作业布置
第4课时 练习课
比 例
表示两个比相等的式子叫做比例。
15∶9 =
20∶12
两个比用等于号连接。
2.4
1.6
60
40
=
分数形式的比
用字母表示:
a∶b=c∶d(b,d≠0)
=
或
b
a
d
c
一、复习回顾
什么是比例?
求比例中的未知项,叫做解比例。
先把比例转化成外项乘积与内项乘积相等的形式(即方程)。
解比例的方法:根据比例的基本性质解比例。
再通过解方程求出未知项的值。
一、复习回顾
什么叫做解比例?解比例的依据是什么?
在比例里,两个外项积等于两个内向积,叫做比例的基本性质。
内项
外项
3 ∶ 9 = 1.2 ∶ 3.6
外项在两端,内项在中间,不要记混哦!
=
1.6
2.5
8
12.5
分子分母交叉相乘
一、复习回顾
比例的基本性质是什么?
二、指导练习
2.哪组中的四个数可以组成比例?把组成的比例写出来。
(1)4,5,12和15
(2)2,3,4和5
4×15=60
5×12=60
可以组成比例
4:5=12:15
2×5=10
3×4=12
不可以组成比例
练
习
八
二、指导练习
(3)1.6,6.4,2和5
(4) 和
1.6×6.4=10.24
5×2=10
不可以组成比例
可以组成比例
2.哪组中的四个数可以组成比例?把组成的比例写出来。
练
习
八
6.小红说得对吗?
那1分钟跳72次。
我的心脏45秒跳54次。
小红
54∶45=????????
?
72∶60=????????
?
答:小红说的对。
比值相等
二、指导练习
练
习
八
7.已知24×3=8×9,根据比例的基本性质,把等式改写比例。
8∶24=3∶9
9∶24=3∶8
8∶3=24∶9
9∶3=24∶8
24∶8=9∶3
24∶9=8∶3
3∶8=9∶24
3∶9=8∶24
24和3作外项,8和9作内项
8和9作外项,24和3作内项
二、指导练习
练
习
八
二、指导练习
8.解比例。
(1)
(2)0.8:4=x:8
解:
解:4x=0.8×8
4x=6.4
x=1.6
练
习
八
二、指导练习
(3)
(4)
解:3x=12×
3x=9
x=3
解:2x=9×8
2x=72
x=36
8.解比例。
练
习
八
11.汽车厂按1∶20的比例生产了一批汽车模型。
(1)轿车模型长24.3 cm,轿车的实际长度是多少?
解:设轿车的实际长度是x cm。
24.3∶x=1∶20
x=486
486 cm=4.86 m
答:轿车的实际长度是4.86 m。
两个比所对应的前后项的量是一致的哦!
二、指导练习
练
习
八
(2)公共汽车长11.76 cm,模型车的长度是多少?
解:设模型车的长度是y m。
y∶11.76=1∶20
y=0.588
0.588 m=58.8 cm
答:模型车的长度是58.8 cm。
二、指导练习
11.汽车厂按1∶20的比例生产了一批汽车模型。
练
习
八
12.博物馆展出了一个高为19.6cm的秦代将军俑模型,它的高度与实际高度的比是1∶10。这个将军俑的实际高度是多少?
解:设将军俑的实际高度是x cm。
19.6∶x=1∶10
x=196
答:将军俑的实际高度是196 cm。
三、巩固练习
练
习
八
三、巩固练习
13.育新小区1号楼的实际高度为35 m,它的高度与模型高度的比是500:1。模型的高度是多少厘米?
解:设模型的高度是x cm。
3500:x=500:1
35 m=3500 cm
500x=3500
x=7
答:模型的高度是7 cm。
练
习
八
14.把下列等式改写成比例。
(1)3×40=8×15
(2)2.5×0.4=0.5×2
3:8=15:40
3:15=8:40
8:3=40:15
15:3=40:8
2.5:0.5=2:0.4
2.5:2=0.5:0.4
0.5:2.5=0.4:2
2:2.5=0.4:0.5
三、巩固练习
练
习
八
……
……
15.李老师买了6个足球和8个篮球,买两种球所花钱数相等。
(1)足球与篮球的单价之比是多少?
三、巩固练习
足球的单价:篮球的单价=8:6
足球的单价:篮球的单价=8:6=4:3
足球的单价×数量=篮球的单价×数量
练
习
八
(2)足球的单价是40元,篮球的单价是多少?
40∶ x=8∶6
解:设篮球的单价是x元。
8x=40×6
x=30
答:篮球的单价是30元。
三、巩固练习
练
习
八
15.李老师买了6个足球和8个篮球,买两种球所花钱数相等。
1.表示两个比相等的式子叫做比例。
2.求比例中的未知项,叫做解比例。
3.在比例里,两个外项的积等于两个内项的积,
这叫做比例的基本性质。
四、课堂小结
作业:
五、作业布置
