八年级数学下册课件-17.1 勾股定理1-人教版(共23张ppt)
文档属性
| 名称 | 八年级数学下册课件-17.1 勾股定理1-人教版(共23张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 17:58:32 | ||
图片预览



文档简介
人教版《数学》八年级下册
学习目标
1、能验证并证明勾股定理;
2、能利用勾股定理解决一些简单的计算问题;
17.1勾股定理(1)
此图是2002年第24届国际数学家大会的会徽的
图案,而国际数学家大会是最高水平的全球性数学
学术会议,选择此图作为会徽一定有其中的道理。
(1)它由哪些基本图形组成?
(2)之前研究过有关直角三角形
的哪些知识?
17.1勾股定理(1)
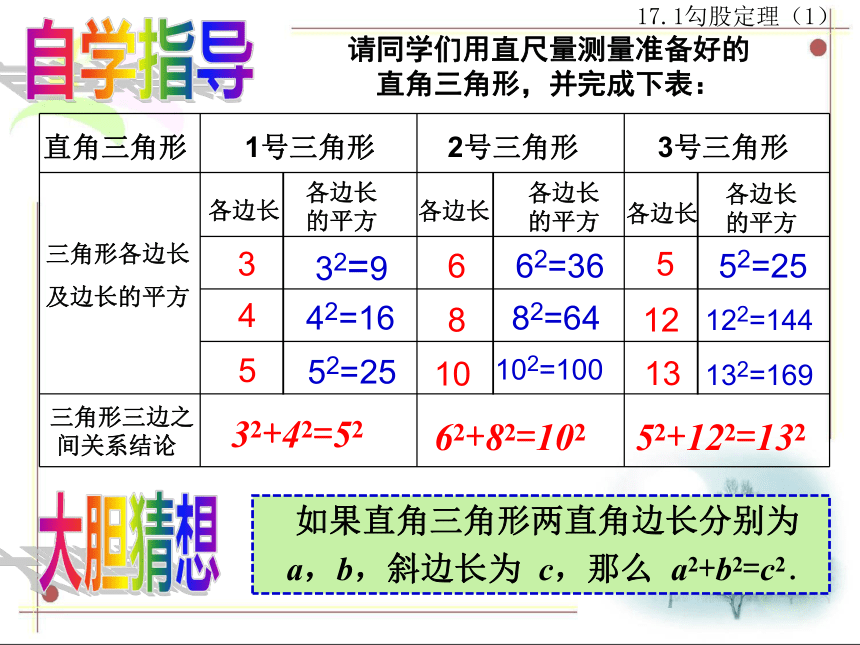
请同学们用直尺量测量准备好的
直角三角形,并完成下表:
直角三角形
1号三角形
2号三角形
3号三角形
三角形三边之
间关系结论
三角形各边长及边长的平方
各边长
各边长
的平方
各边长
各边长
各边长
的平方
各边长
的平方
如果直角三角形两直角边长分别为
a,b,斜边长为 c,那么 a2+b2=c2.
3
4
5
32=9
42=16
52=25
32+42=52
6
8
10
62=36
82=64
102=100
62+82=102
5
12
13
52=25
122=144
132=169
52+122=132
17.1勾股定理(1)
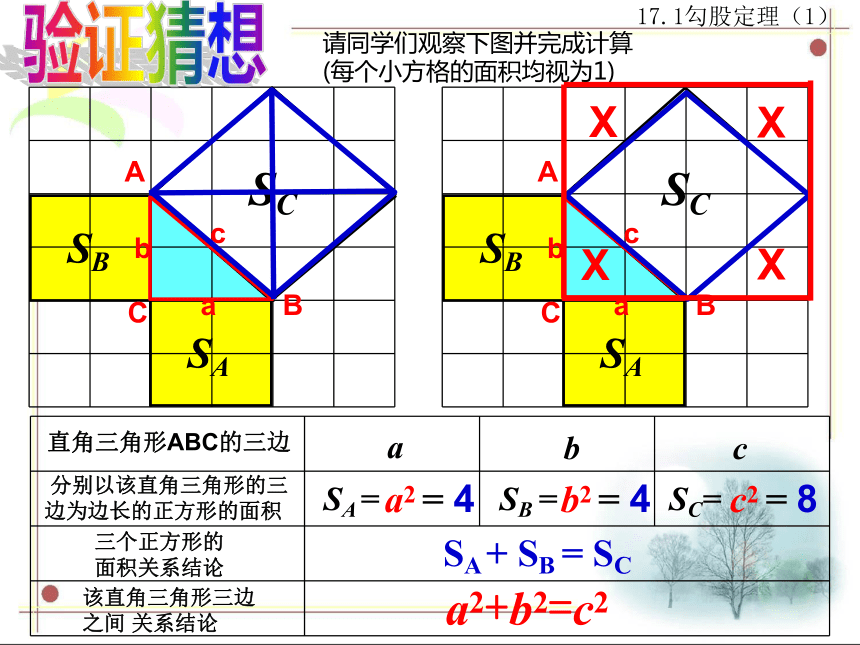
请同学们观察下图并完成计算
(每个小方格的面积均视为1)
冯绍峰
直角三角形ABC的三边
分别以该直角三角形的三
边为边长的正方形的面积
三个正方形的
面积关系结论
该直角三角形三边之间 关系结论
a
c
b
SA =
SB =
SC=
a
b
c
SA
SB
SC
A
B
C
a
b
c
SA
SB
SC
A
B
C
a2 = 4
SA + SB = SC
b2 = 4
c2 = 8
a2+b2=c2
X
X
X
X
17.1勾股定理(1)
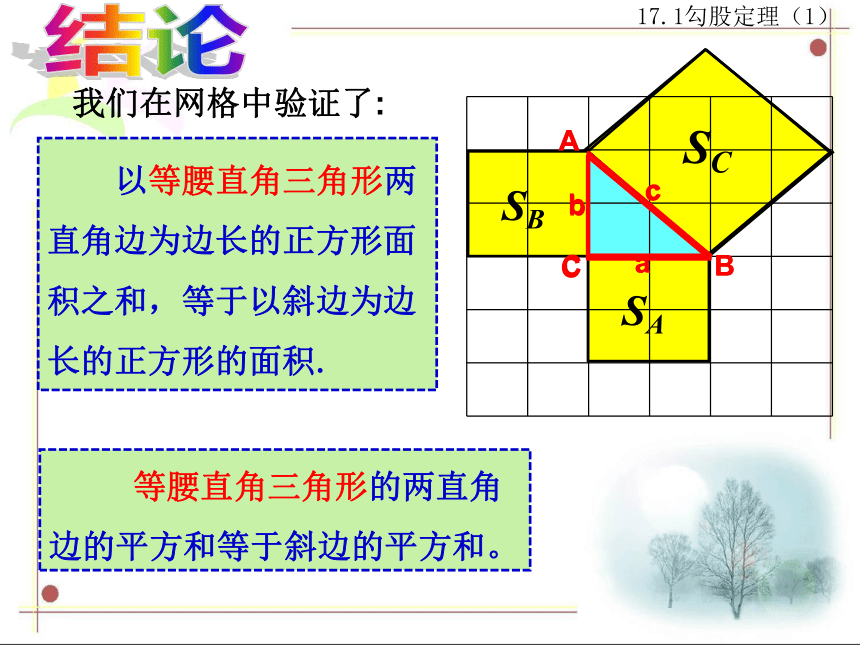
以等腰直角三角形两直角边为边长的正方形面积之和,等于以斜边为边长的正方形的面积.
等腰直角三角形的两直角边的平方和等于斜边的平方和。
a
b
c
SA
SB
A
B
C
SC
我们在网格中验证了:
a
b
c
A
B
C
17.1勾股定理(1)
冯绍峰
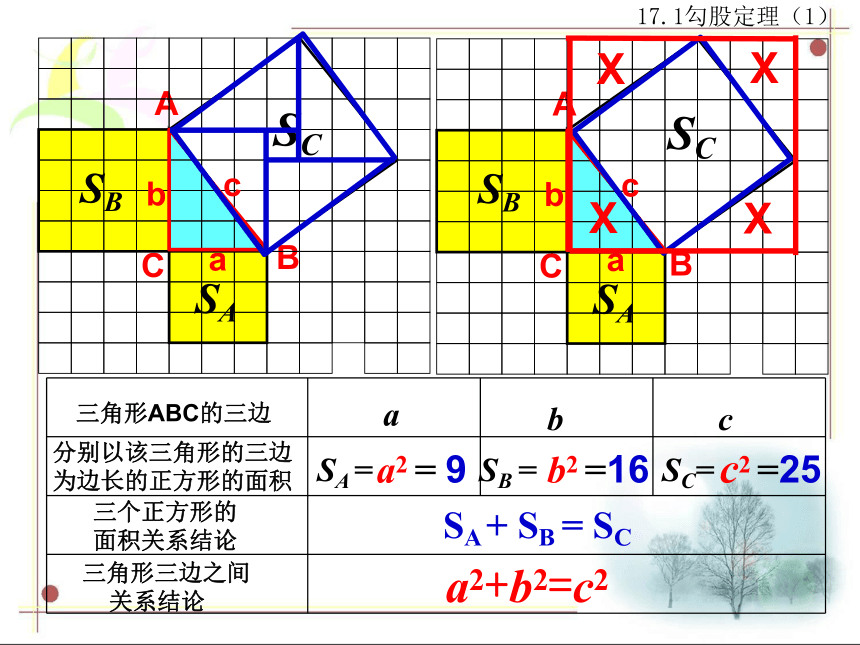
三角形ABC的三边
分别以该三角形的三边
为边长的正方形的面积
三个正方形的
面积关系结论
三角形三边之间
关系结论
a
c
b
SA =
SB =
SC=
A
C
B
a
b
c
SA
SB
SC
A
C
B
a
b
c
SA
SB
SC
a2 = 9
b2 =16
c2 =25
X
X
X
X
SA + SB = SC
a2+b2=c2
17.1勾股定理(1)
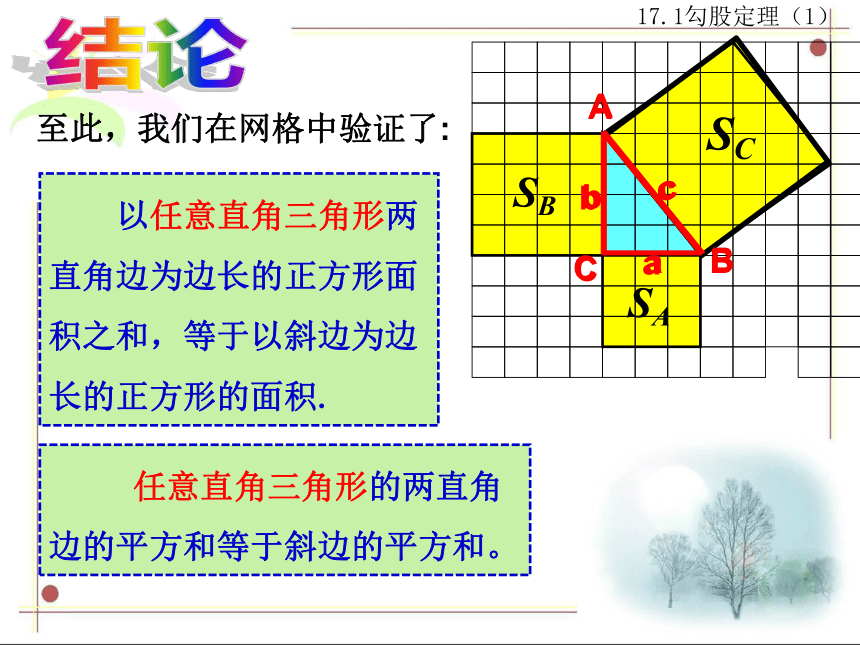
至此,我们在网格中验证了:
任意直角三角形的两直角边的平方和等于斜边的平方和。
以任意直角三角形两直角边为边长的正方形面积之和,等于以斜边为边长的正方形的面积.
A
C
B
a
b
c
SA
SB
SC
A
C
B
a
b
c
17.1勾股定理(1)
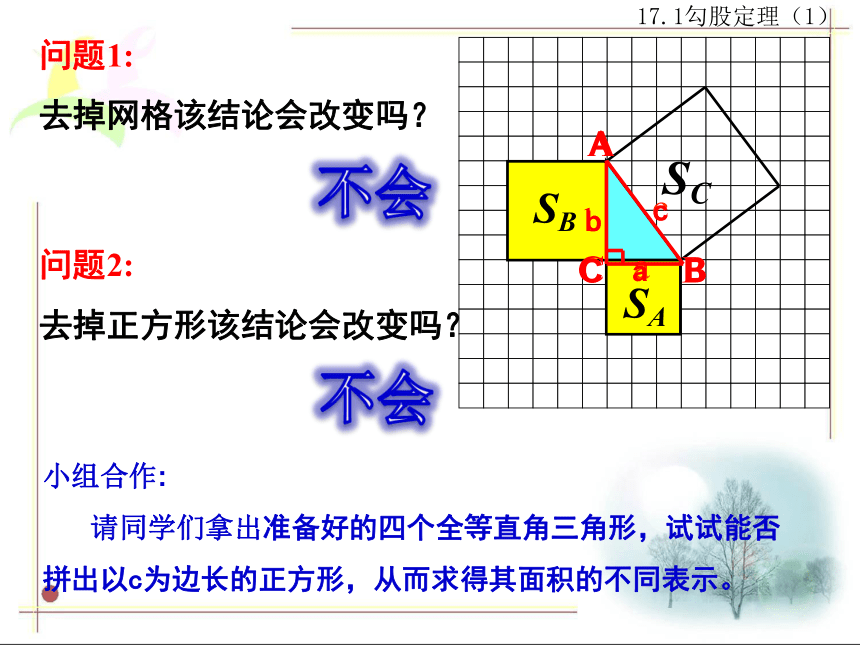
问题1:
去掉网格该结论会改变吗?
问题2:
去掉正方形该结论会改变吗?
A
B
C
a
b
c
SA
SB
SC
c
a
b
C
A
B
小组合作:
请同学们拿出准备好的四个全等直角三角形,试试能否
拼出以c为边长的正方形,从而求得其面积的不同表示。
17.1勾股定理(1)
A
C
B
a
b
c
a
c
b
a
c
b
a
c
b
a
c
b
c2 =
=b2-2ab+a2+ 2ab
=a2+b2
∴ a2+b2=c2.
以直角三角形两直角边为边长的正方形的面积之和为 ______ ;
以该直角三角形的斜边为边长的正方形的面积为______ ;
c2
a2+b2
17.1勾股定理(1)
A
C
B
a
b
c
a
c
b
a
c
b
a
c
b
a
c
b
=a2+2ab+b2 - 2ab
∴ c2 = a2+b2.
(a+b)2 -
以直角三角形两直角边为边长的正方形的面积之和为 ______ ;
以该直角三角形的斜边为边长的正方形的面积为______ ;
c2
a2+b2
C2 =
= a2+b2.
17.1勾股定理(1)
现在,我们已经证明了猜想的正确性,在数学上经过证明被确认为正确的命题叫做定理,该定理在我国叫做勾股定理.
直角三角形两直角边的平方和等于斜边的平方.
如果直角三角形两直角边长分别为
a, b,斜边长为c,那么a2+b2=c2.
勾股定理
A
C
B
a
b
c
即:
17.1勾股定理(1)
为什么叫勾股定理这个名称呢?
勾
股
国外又叫毕达哥拉斯定理
原来在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.于是我国古代学者就把直角三角形中较短直角边称为“勾”,较长直角边称为“股”,斜边称为“弦”.由于此命题反映的正好是直角三角形三边的关系,所以叫做勾股定理.
17.1勾股定理(1)
c
b
a
这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》
时给出的,人们称它为“赵爽弦图”. 赵爽根据此图指出:四个
全等的直角三角形(红色)可以如图 围成一个大正方形, 中间
的部分是一个小正方形 (黄色).勾股定理在数学发展中起到
了重大的作用,其证明方法据说
有400 多种,有兴趣的同学可以
继续研究,或到网上查阅勾股定
理的相关资料.
17.1勾股定理(1)
c
b
a
a2
b2
c2 = a2+b2
17.1勾股定理(1)
c
b
a
a2
b2
c2 = a2+b2
17.1勾股定理(1)
1、求图中字母所代表的正方形的面积.
A
A
A
B
225
144
80
24
17
8
2、设直角三角形的两直角边分别为a,b, 斜边为c.
(1)已知 a=5, b=12, 求 c;
(2)已知 a=6, c=10, 求 b;
(3)已知 c=25, b=15, 求 a;
17.1勾股定理(1)
(1)若已知 a, b, 则
(2)若已知 a, c, 则
(3)若已知 c, b, 则
如果直角三角形两直角边长分别为
a, b,斜边长为c,那么a2+b2=c2.
勾股定理
A
C
B
a
b
c
17.1勾股定理(1)
一、必做题:
(1)课本第24页练习题第2题;
(2)课本第28页复习巩固第1题;
二、选做题:
1. 如图,在边长为1个单位长度的小正方形
组成的网格中,点A、B都是格点,则线段
AB的长度为( )
A.5 B.6 C.7 D.25
2. 一直角三角形的两边长是6和8, 则第三边长为________;
3. 在△ABC中,∠C=900, 若AB=6, 则AB2+BC2+AC2 =______;
17.1勾股定理(1)
课本第24页练习2
2、如图,所有的三角形都是直角三角形,四边形都是
正方形,已知正方形 A,B,C,D 的
边长分别是 12, 16, 9, 12.
求最大正方形 E 的面积.
A
B
C
D
E
17.1勾股定理(1)
通过这种方法,可以把一个正方形的面积分成
若干个小正方形的面积的和,不断地分下去,就可
以得到一棵美丽的勾股树.
17.1勾股定理(1)
学习目标
1、能验证并证明勾股定理;
2、能利用勾股定理解决一些简单的计算问题;
17.1勾股定理(1)
此图是2002年第24届国际数学家大会的会徽的
图案,而国际数学家大会是最高水平的全球性数学
学术会议,选择此图作为会徽一定有其中的道理。
(1)它由哪些基本图形组成?
(2)之前研究过有关直角三角形
的哪些知识?
17.1勾股定理(1)
请同学们用直尺量测量准备好的
直角三角形,并完成下表:
直角三角形
1号三角形
2号三角形
3号三角形
三角形三边之
间关系结论
三角形各边长及边长的平方
各边长
各边长
的平方
各边长
各边长
各边长
的平方
各边长
的平方
如果直角三角形两直角边长分别为
a,b,斜边长为 c,那么 a2+b2=c2.
3
4
5
32=9
42=16
52=25
32+42=52
6
8
10
62=36
82=64
102=100
62+82=102
5
12
13
52=25
122=144
132=169
52+122=132
17.1勾股定理(1)
请同学们观察下图并完成计算
(每个小方格的面积均视为1)
冯绍峰
直角三角形ABC的三边
分别以该直角三角形的三
边为边长的正方形的面积
三个正方形的
面积关系结论
该直角三角形三边之间 关系结论
a
c
b
SA =
SB =
SC=
a
b
c
SA
SB
SC
A
B
C
a
b
c
SA
SB
SC
A
B
C
a2 = 4
SA + SB = SC
b2 = 4
c2 = 8
a2+b2=c2
X
X
X
X
17.1勾股定理(1)
以等腰直角三角形两直角边为边长的正方形面积之和,等于以斜边为边长的正方形的面积.
等腰直角三角形的两直角边的平方和等于斜边的平方和。
a
b
c
SA
SB
A
B
C
SC
我们在网格中验证了:
a
b
c
A
B
C
17.1勾股定理(1)
冯绍峰
三角形ABC的三边
分别以该三角形的三边
为边长的正方形的面积
三个正方形的
面积关系结论
三角形三边之间
关系结论
a
c
b
SA =
SB =
SC=
A
C
B
a
b
c
SA
SB
SC
A
C
B
a
b
c
SA
SB
SC
a2 = 9
b2 =16
c2 =25
X
X
X
X
SA + SB = SC
a2+b2=c2
17.1勾股定理(1)
至此,我们在网格中验证了:
任意直角三角形的两直角边的平方和等于斜边的平方和。
以任意直角三角形两直角边为边长的正方形面积之和,等于以斜边为边长的正方形的面积.
A
C
B
a
b
c
SA
SB
SC
A
C
B
a
b
c
17.1勾股定理(1)
问题1:
去掉网格该结论会改变吗?
问题2:
去掉正方形该结论会改变吗?
A
B
C
a
b
c
SA
SB
SC
c
a
b
C
A
B
小组合作:
请同学们拿出准备好的四个全等直角三角形,试试能否
拼出以c为边长的正方形,从而求得其面积的不同表示。
17.1勾股定理(1)
A
C
B
a
b
c
a
c
b
a
c
b
a
c
b
a
c
b
c2 =
=b2-2ab+a2+ 2ab
=a2+b2
∴ a2+b2=c2.
以直角三角形两直角边为边长的正方形的面积之和为 ______ ;
以该直角三角形的斜边为边长的正方形的面积为______ ;
c2
a2+b2
17.1勾股定理(1)
A
C
B
a
b
c
a
c
b
a
c
b
a
c
b
a
c
b
=a2+2ab+b2 - 2ab
∴ c2 = a2+b2.
(a+b)2 -
以直角三角形两直角边为边长的正方形的面积之和为 ______ ;
以该直角三角形的斜边为边长的正方形的面积为______ ;
c2
a2+b2
C2 =
= a2+b2.
17.1勾股定理(1)
现在,我们已经证明了猜想的正确性,在数学上经过证明被确认为正确的命题叫做定理,该定理在我国叫做勾股定理.
直角三角形两直角边的平方和等于斜边的平方.
如果直角三角形两直角边长分别为
a, b,斜边长为c,那么a2+b2=c2.
勾股定理
A
C
B
a
b
c
即:
17.1勾股定理(1)
为什么叫勾股定理这个名称呢?
勾
股
国外又叫毕达哥拉斯定理
原来在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.于是我国古代学者就把直角三角形中较短直角边称为“勾”,较长直角边称为“股”,斜边称为“弦”.由于此命题反映的正好是直角三角形三边的关系,所以叫做勾股定理.
17.1勾股定理(1)
c
b
a
这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》
时给出的,人们称它为“赵爽弦图”. 赵爽根据此图指出:四个
全等的直角三角形(红色)可以如图 围成一个大正方形, 中间
的部分是一个小正方形 (黄色).勾股定理在数学发展中起到
了重大的作用,其证明方法据说
有400 多种,有兴趣的同学可以
继续研究,或到网上查阅勾股定
理的相关资料.
17.1勾股定理(1)
c
b
a
a2
b2
c2 = a2+b2
17.1勾股定理(1)
c
b
a
a2
b2
c2 = a2+b2
17.1勾股定理(1)
1、求图中字母所代表的正方形的面积.
A
A
A
B
225
144
80
24
17
8
2、设直角三角形的两直角边分别为a,b, 斜边为c.
(1)已知 a=5, b=12, 求 c;
(2)已知 a=6, c=10, 求 b;
(3)已知 c=25, b=15, 求 a;
17.1勾股定理(1)
(1)若已知 a, b, 则
(2)若已知 a, c, 则
(3)若已知 c, b, 则
如果直角三角形两直角边长分别为
a, b,斜边长为c,那么a2+b2=c2.
勾股定理
A
C
B
a
b
c
17.1勾股定理(1)
一、必做题:
(1)课本第24页练习题第2题;
(2)课本第28页复习巩固第1题;
二、选做题:
1. 如图,在边长为1个单位长度的小正方形
组成的网格中,点A、B都是格点,则线段
AB的长度为( )
A.5 B.6 C.7 D.25
2. 一直角三角形的两边长是6和8, 则第三边长为________;
3. 在△ABC中,∠C=900, 若AB=6, 则AB2+BC2+AC2 =______;
17.1勾股定理(1)
课本第24页练习2
2、如图,所有的三角形都是直角三角形,四边形都是
正方形,已知正方形 A,B,C,D 的
边长分别是 12, 16, 9, 12.
求最大正方形 E 的面积.
A
B
C
D
E
17.1勾股定理(1)
通过这种方法,可以把一个正方形的面积分成
若干个小正方形的面积的和,不断地分下去,就可
以得到一棵美丽的勾股树.
17.1勾股定理(1)
