八年级数学下册课件-18.1.2 平行四边形的判定(20张PPT)
文档属性
| 名称 | 八年级数学下册课件-18.1.2 平行四边形的判定(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 00:00:00 | ||
图片预览



文档简介
18.1.2平行四边形的判定
八年级数学下册
(新人教版)
知识与技能:
掌握平行四边形的判定方法1,2,3,能用它们来证明一个四边形是否是平行四边形.
过程与方法:
在观察、实验、猜想、验证、推理、交流等活动过程中,让学生感受数学思考过程的条理性及解决问题策略的多样性,发展学生的动手操作能力,推理能力及数学应用意识.
情感态度与价值观:
在操作活动和观察、分析过程中发展学生的主动探索、质疑和独立思考的习惯,发展学生的实践能力和创新意识.
教学重点:
平行四边形的判定方法1,2,3.
教学难点:
平行四边形判定方法的探寻过程
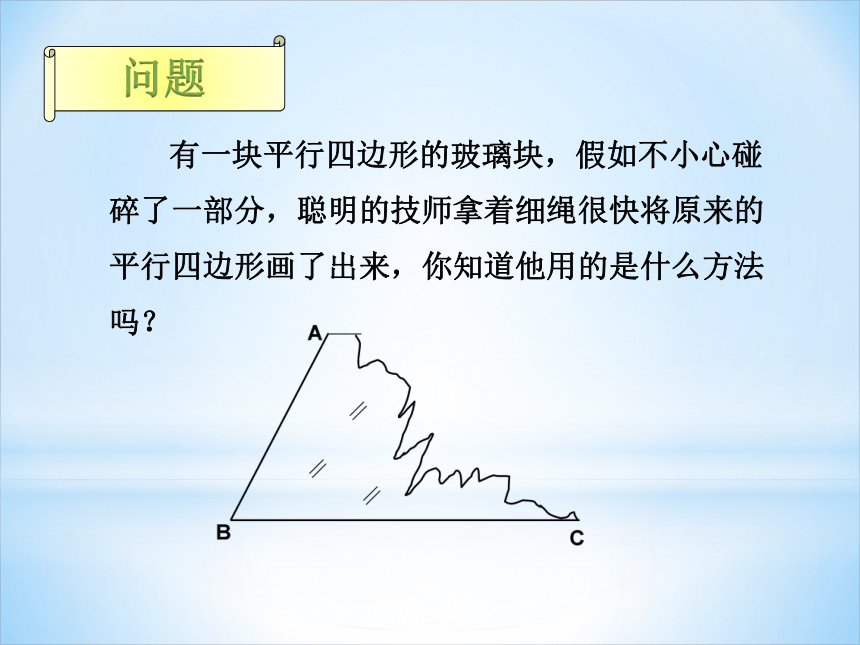
有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
D
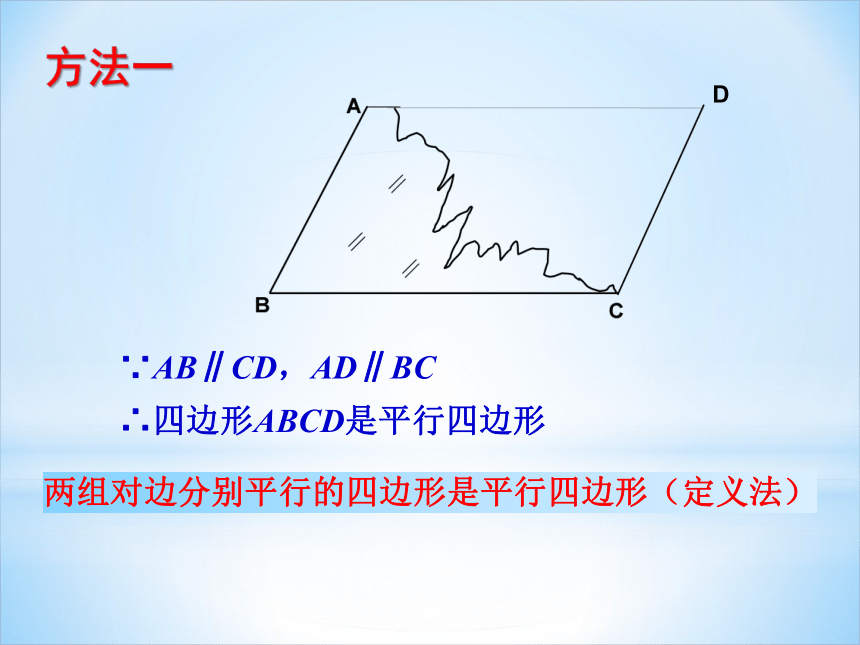
两组对边分别平行的四边形是平行四边形(定义法)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
方法一
D
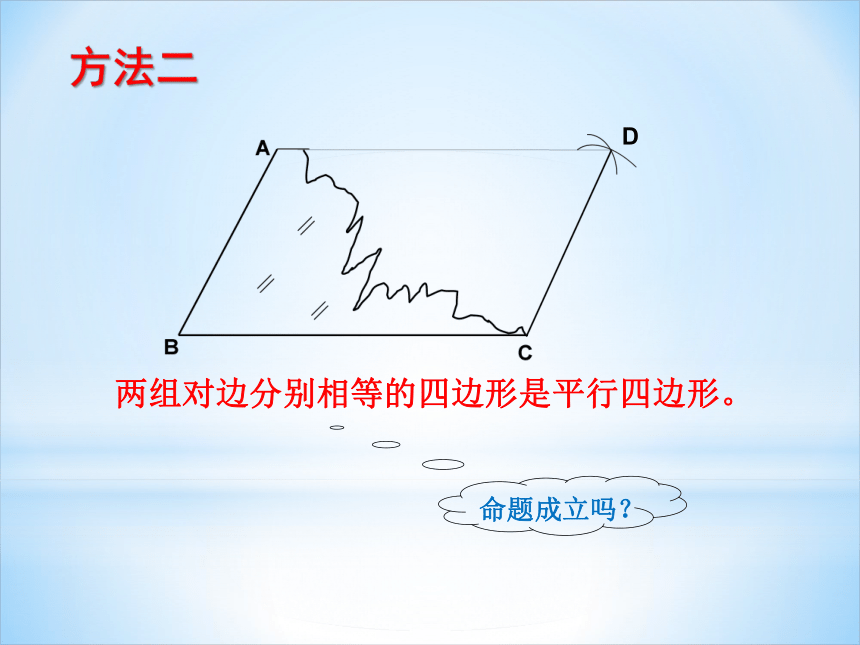
两组对边分别相等的四边形是平行四边形。
方法二
命题成立吗?
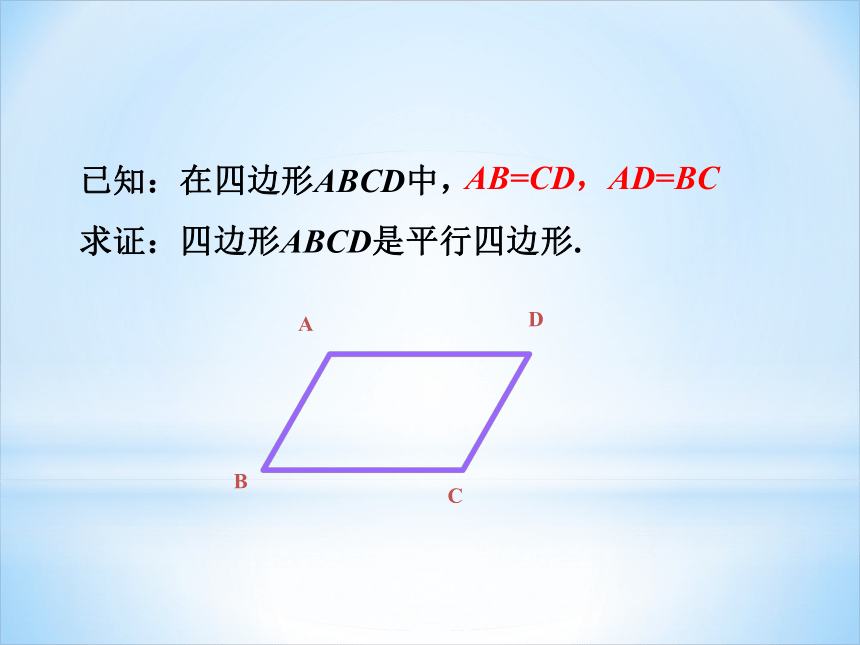
已知:在四边形ABCD中,
求证:四边形ABCD是平行四边形.
AB=CD,AD=BC
D
B
A
C
D
B
A
C
2
1
3
4
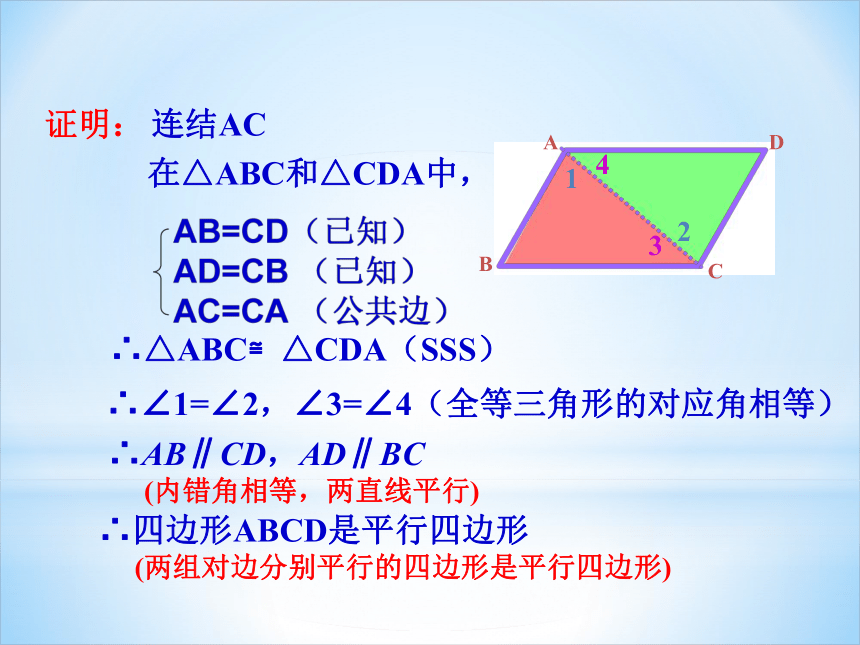
证明:
连结AC
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
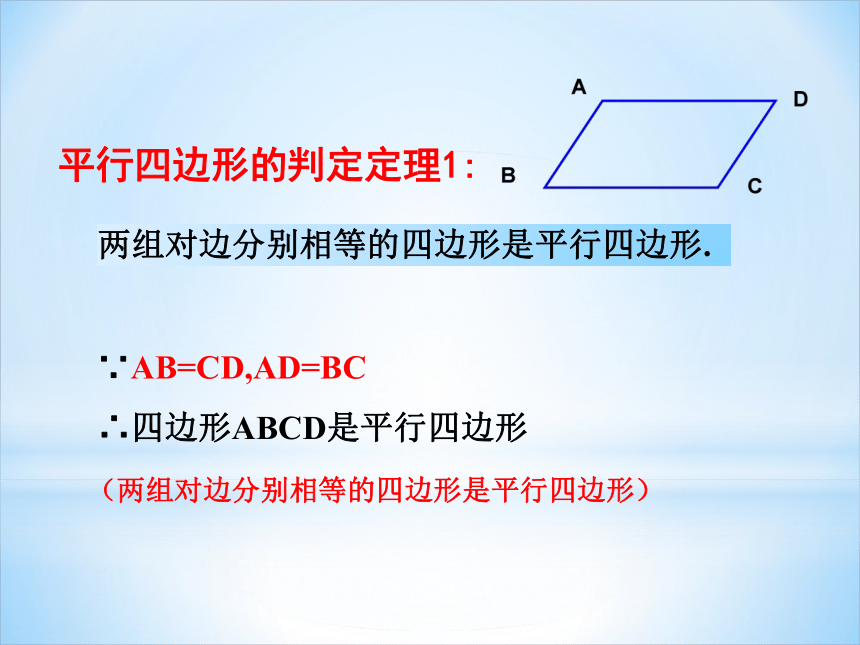
两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理1:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
方法三
D
一组对边平行且相等的四边形是平行四边形。
命
题
成
立
吗
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
在ΔABC与ΔCDA中
∴ΔABC≌ΔCDA(SAS)
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
AD=BC
∠DAC=∠ACB
AC=AC
一组对边平行且相等的四边形是平行四边形.
平行四边形的判定定理2:
∵AB CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
D
两组对角分别相等的四边形是平行四边形。
方法四
命题成立吗?
已知:四边形ABCD,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
证明:
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180°
∴ AD∥BC(同旁内角互补,两直线平行)
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理3:
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形)
D
O
对角线互相平分的四边形是平行四边形。
方法五
命题成立吗?
O
B
A
C
2
1
D
已知:四边形ABCD, 对角线AC、BD相交于点O,
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
对角线互相平分的四边形是平行四边形
平行四边形的判定定理4:
O
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
从边来判定
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
总结
八年级数学下册
(新人教版)
知识与技能:
掌握平行四边形的判定方法1,2,3,能用它们来证明一个四边形是否是平行四边形.
过程与方法:
在观察、实验、猜想、验证、推理、交流等活动过程中,让学生感受数学思考过程的条理性及解决问题策略的多样性,发展学生的动手操作能力,推理能力及数学应用意识.
情感态度与价值观:
在操作活动和观察、分析过程中发展学生的主动探索、质疑和独立思考的习惯,发展学生的实践能力和创新意识.
教学重点:
平行四边形的判定方法1,2,3.
教学难点:
平行四边形判定方法的探寻过程
有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
D
两组对边分别平行的四边形是平行四边形(定义法)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
方法一
D
两组对边分别相等的四边形是平行四边形。
方法二
命题成立吗?
已知:在四边形ABCD中,
求证:四边形ABCD是平行四边形.
AB=CD,AD=BC
D
B
A
C
D
B
A
C
2
1
3
4
证明:
连结AC
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴AB∥CD,AD∥BC
(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理1:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
方法三
D
一组对边平行且相等的四边形是平行四边形。
命
题
成
立
吗
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
在ΔABC与ΔCDA中
∴ΔABC≌ΔCDA(SAS)
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
AD=BC
∠DAC=∠ACB
AC=AC
一组对边平行且相等的四边形是平行四边形.
平行四边形的判定定理2:
∵AB CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
D
两组对角分别相等的四边形是平行四边形。
方法四
命题成立吗?
已知:四边形ABCD,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
证明:
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180°
∴ AD∥BC(同旁内角互补,两直线平行)
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理3:
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形)
D
O
对角线互相平分的四边形是平行四边形。
方法五
命题成立吗?
O
B
A
C
2
1
D
已知:四边形ABCD, 对角线AC、BD相交于点O,
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
对角线互相平分的四边形是平行四边形
平行四边形的判定定理4:
O
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
从边来判定
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
总结
