八年级数学下册课件-18.1.2 平行四边形的判定52-人教版(共19张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.1.2 平行四边形的判定52-人教版(共19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 904.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 18:00:08 | ||
图片预览

文档简介
18.1.2
平行四边形的判定
第3课时
第十八章
平行四边形
18.1
平行四边形
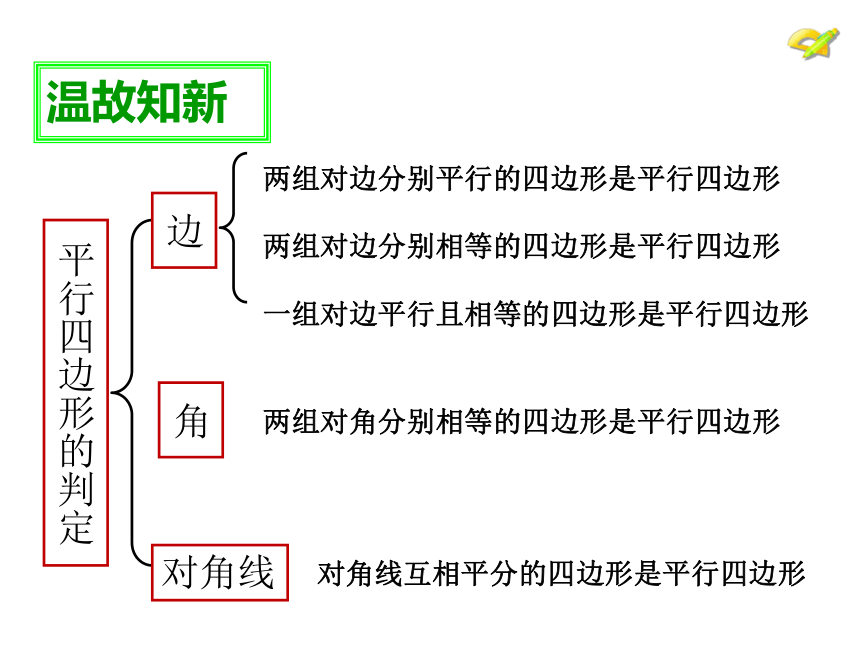
温故知新
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
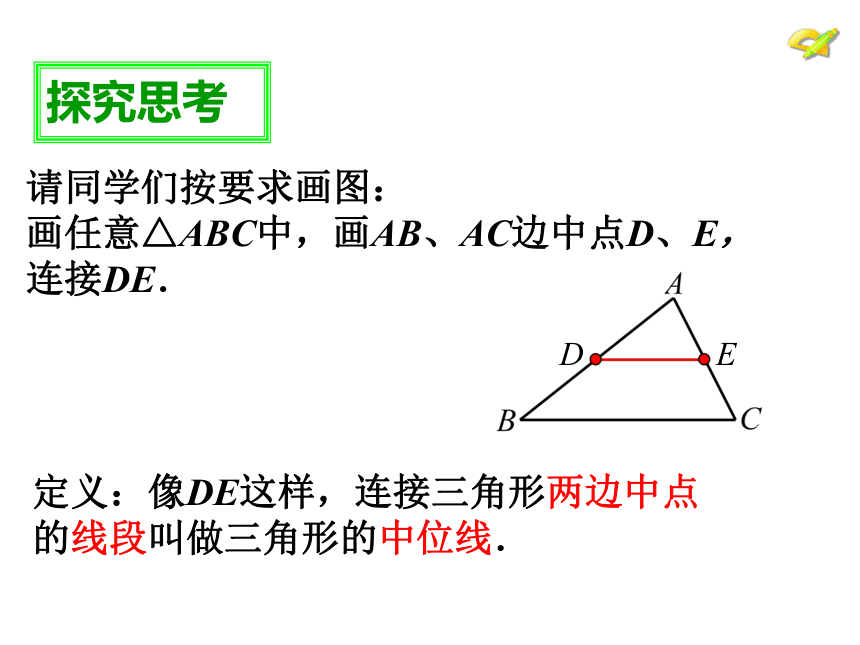
探究思考
请同学们按要求画图:
画任意△ABC中,画AB、AC边中点D、E,
连接DE.
D
E
定义:像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
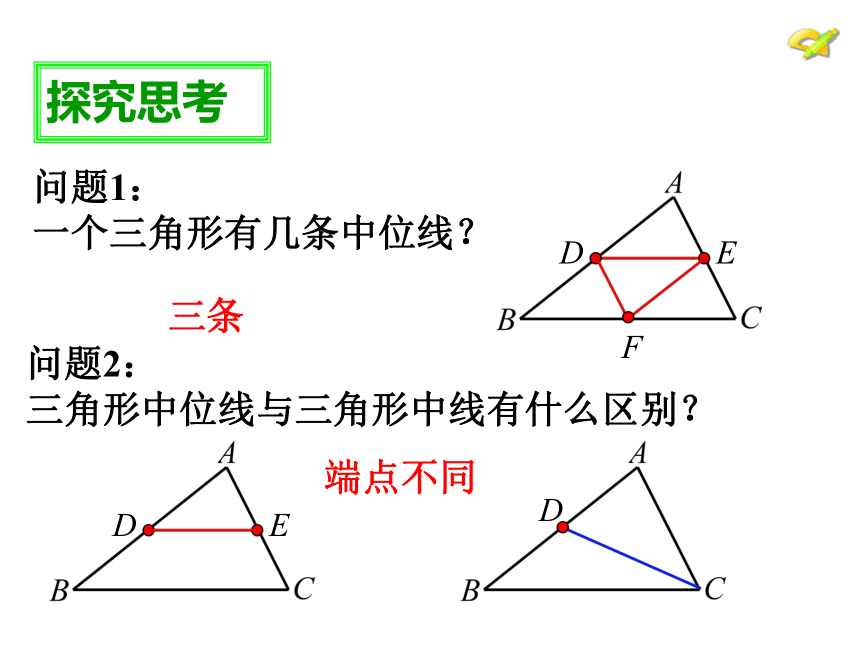
探究思考
问题1:
一个三角形有几条中位线?
D
E
F
三条
问题2:
三角形中位线与三角形中线有什么区别?
D
E
D
端点不同
探究思考
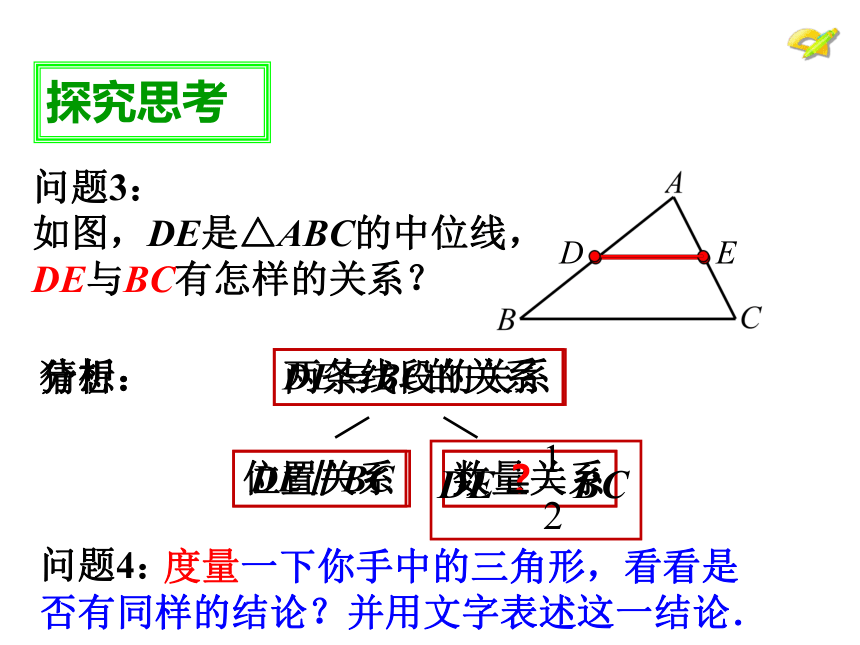
问题3:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
问题4:
探究思考
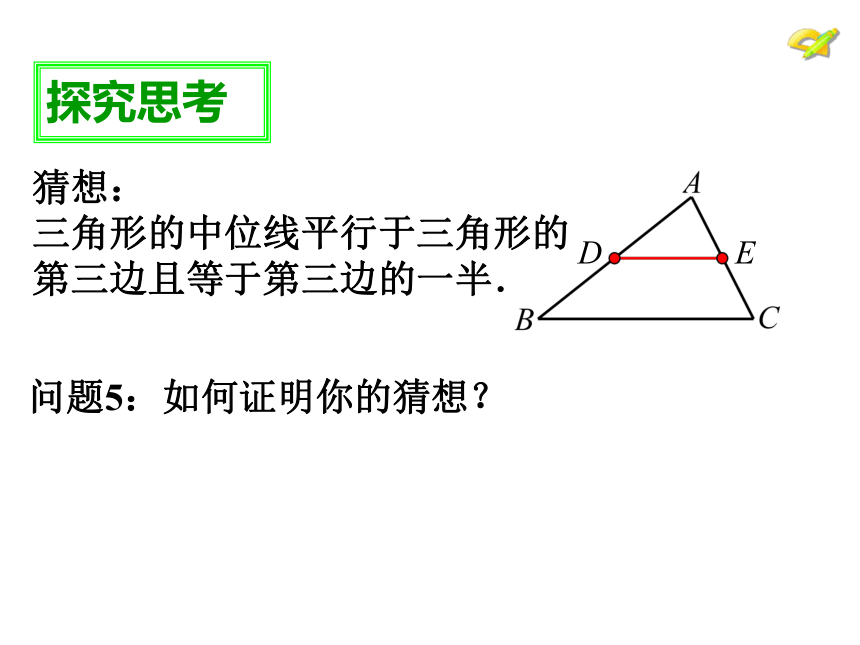
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
问题5:如何证明你的猜想?
探究思考
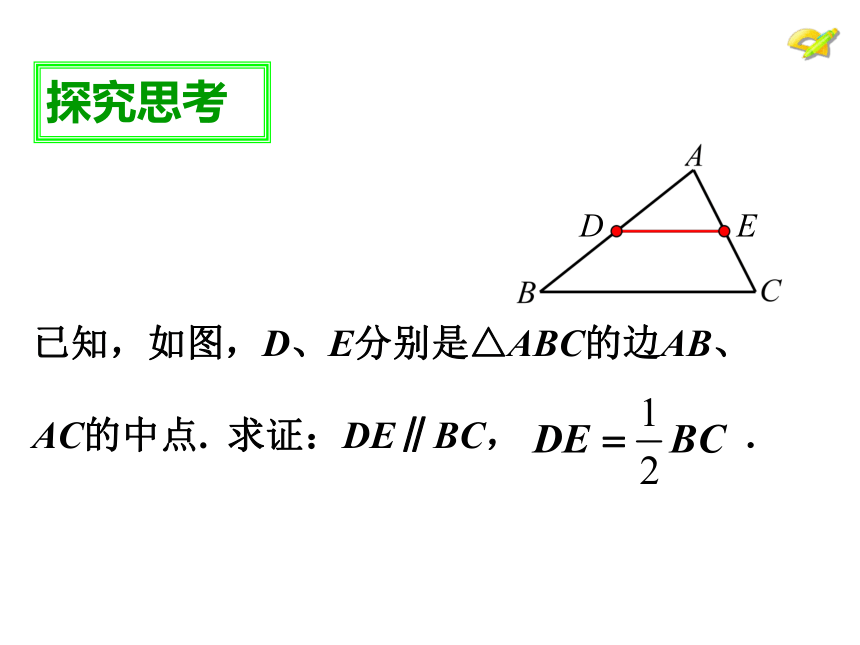
已知,如图,D、E分别是△ABC的边AB、
AC的中点.
求证:DE∥BC,
.
D
E
探究思考
平行
角
平行四边形
或
线段相等
一条线段是另一条线段的一半
倍长短线
分析1:
D
E
探究思考
分析2:
D
E
互相平分
构造
平行四边形
倍长DE
探究思考
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC
.
∵AE=EC,DE=EF
,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
证法1:
∴CF
AD
.
∴CF
BD
.
探究思考
证明:
D
E
∴
DE∥BC,
.
F
又
,
∴DF
BC
.
D
E
探究思考
证明:
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE,
(下面证明同证法1)
证法2:
,AD
CF.
∴BD
CF.
探究思考
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE=
BC.
三角形中位线定理:
符号语言:
探究思考
D
E
三角形的中位线
平行
一条线段是另一条线段的2倍或
三角形中位线定理:
学以致用
1.
如图,△ABC中,D、E分别是AB、AC中点.
(1)
若DE=5,则BC=
.
(2)
若∠B=65°,则∠ADE=
°.
(3)
若DE+BC=12,则BC=
.
10
65
x
2x
x+2x=12
x=4
8
学以致用
2.
如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
学以致用
例:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
连接对角线
三角形问题
(三角形中位线定理)
归纳小结
知识方面:三角形中位线概念;
三角形中位线定理.
思想方法方面:转化思想.
布置作业
必做题:教材第49页练习第1、2题.
选做题:再顺次连接本节课例题中所得到的四边形EFGH各边中点,又得到一个新的四边形,判断这个新四边形是否是平行四边形,并说明理由.
