八年级数学下册课件-20.2 数据的波动程度2-人教版(共12张ppt)
文档属性
| 名称 | 八年级数学下册课件-20.2 数据的波动程度2-人教版(共12张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 00:00:00 | ||
图片预览





文档简介
数据的波动程度
第二课时
一、复习旧知,引入新知
甲、乙两名运动员在10次百米跑练习中的成绩(单位:秒)如下:
甲:10.8、10.9、11.0、10.7、11.2、11.1、10.8、
11.0、10.7、10.9;
乙:10.9、10.9、10.8、10.8、11.0、10.9、10.8、
11.1、10.9、10.8.
分别计算出这两名运动员成绩的平均数和方差,根据你的计算判断谁的成绩更稳定?
x甲=10.91;s2甲=0.0249。
x乙=10.89;s2乙=0.0089。
∵s2甲>s2乙 , ∴乙的成绩更稳定。
【答】
1. MODE + 2-SD 进入SD模式;
2. SHIFT + CLR + =清除统计存储器;
3. 输入数据,每输入一个数据后按 DT ;
4. SHIFT + S-Var + xσn + = ;
5. 将求出的结果平方,就得到方差 。
二、学习新知,完善方法
例如:计算上题中甲的方差。
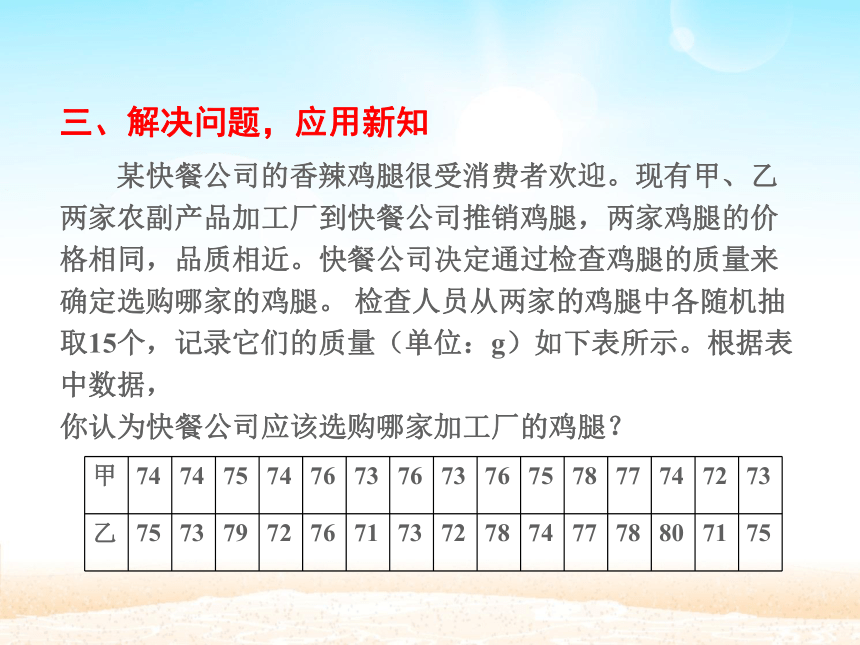
三、解决问题,应用新知
某快餐公司的香辣鸡腿很受消费者欢迎。现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近。快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿。 检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如下表所示。根据表中数据,
你认为快餐公司应该选购哪家加工厂的鸡腿?
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
解析:甲、乙两家的鸡腿质量的平均数分别是:
x甲≈75,x乙≈75。
方差分别是s2甲≈3,s2乙≈8。
s2甲< s2乙
由此可知,快餐公司应该选购甲加工厂生产的鸡腿。
四、课堂闯关,自主反馈
某跳远队准备从甲、乙两名运动员中选取成绩稳定的一名参加比赛。下表是这两名运动员10次测验成绩(单位:m):
甲
5.85
5.93
6.07
5.91
5.99
6.13
5.98
6.05
6.00
6.19
乙
6.11
6.08
5.83
5.92
5.84
5.81
6.18
6.17
5.85
6.21
你认为应该选择哪名运动员参赛?为什么?
【答】甲、乙测验成绩的平均数分别是
x甲 =6.01 ,x乙= 6。
方差分别是:
s2甲≈0.00954,s2乙≈0.02434。
s2甲< s2乙,因此,应该选甲参加比赛。
五、本课小结
(1)用科学计算器可以优化复杂数据的方差计算问题;
(2)实际问题中常采用用样本方差估计总体方差的统计思想。
六、布置作业
(1)为了考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高(单位:mm)如下:
甲:9,10,11,12,7,13,10,8,12,8
乙:8,13,12,11,10,12,7,7,9,11
请你经过计算后回答如下问题:
①哪种农作物的苗长得较高?
②哪种农作物的苗长得较整齐?
(2)为了从甲、乙两名学生中选拔一人参加射击比赛,现对他们的射击水平进行了检测,两人在相同的条件下各打靶10次,成绩如下:
甲:7,8,6,8,6,5,9,10,7,4;
乙:9,5,7,8,6,8,7,6,7,7。
①求x甲,x乙; s2甲, s2乙;
②你认为应该选拔哪名同学参加射击比赛?为什么?
谢 谢
第二课时
一、复习旧知,引入新知
甲、乙两名运动员在10次百米跑练习中的成绩(单位:秒)如下:
甲:10.8、10.9、11.0、10.7、11.2、11.1、10.8、
11.0、10.7、10.9;
乙:10.9、10.9、10.8、10.8、11.0、10.9、10.8、
11.1、10.9、10.8.
分别计算出这两名运动员成绩的平均数和方差,根据你的计算判断谁的成绩更稳定?
x甲=10.91;s2甲=0.0249。
x乙=10.89;s2乙=0.0089。
∵s2甲>s2乙 , ∴乙的成绩更稳定。
【答】
1. MODE + 2-SD 进入SD模式;
2. SHIFT + CLR + =清除统计存储器;
3. 输入数据,每输入一个数据后按 DT ;
4. SHIFT + S-Var + xσn + = ;
5. 将求出的结果平方,就得到方差 。
二、学习新知,完善方法
例如:计算上题中甲的方差。
三、解决问题,应用新知
某快餐公司的香辣鸡腿很受消费者欢迎。现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近。快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿。 检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如下表所示。根据表中数据,
你认为快餐公司应该选购哪家加工厂的鸡腿?
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
解析:甲、乙两家的鸡腿质量的平均数分别是:
x甲≈75,x乙≈75。
方差分别是s2甲≈3,s2乙≈8。
s2甲< s2乙
由此可知,快餐公司应该选购甲加工厂生产的鸡腿。
四、课堂闯关,自主反馈
某跳远队准备从甲、乙两名运动员中选取成绩稳定的一名参加比赛。下表是这两名运动员10次测验成绩(单位:m):
甲
5.85
5.93
6.07
5.91
5.99
6.13
5.98
6.05
6.00
6.19
乙
6.11
6.08
5.83
5.92
5.84
5.81
6.18
6.17
5.85
6.21
你认为应该选择哪名运动员参赛?为什么?
【答】甲、乙测验成绩的平均数分别是
x甲 =6.01 ,x乙= 6。
方差分别是:
s2甲≈0.00954,s2乙≈0.02434。
s2甲< s2乙,因此,应该选甲参加比赛。
五、本课小结
(1)用科学计算器可以优化复杂数据的方差计算问题;
(2)实际问题中常采用用样本方差估计总体方差的统计思想。
六、布置作业
(1)为了考察甲、乙两种农作物的长势,分别从中抽取了10株苗,测得苗高(单位:mm)如下:
甲:9,10,11,12,7,13,10,8,12,8
乙:8,13,12,11,10,12,7,7,9,11
请你经过计算后回答如下问题:
①哪种农作物的苗长得较高?
②哪种农作物的苗长得较整齐?
(2)为了从甲、乙两名学生中选拔一人参加射击比赛,现对他们的射击水平进行了检测,两人在相同的条件下各打靶10次,成绩如下:
甲:7,8,6,8,6,5,9,10,7,4;
乙:9,5,7,8,6,8,7,6,7,7。
①求x甲,x乙; s2甲, s2乙;
②你认为应该选拔哪名同学参加射击比赛?为什么?
谢 谢
