八年级数学下册课件-18.1.1 平行四边形的性质2-人教版(共30张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.1.1 平行四边形的性质2-人教版(共30张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 18:49:48 | ||
图片预览





文档简介
第十八章 平行四边形
18.1.1 平行四边形的性质
第1课时
自主学习(先自己动手,再小组合作完成下列问题)
1、将一张纸对折,剪下两个完全一样的三角
形纸片,将这两个三角形相等的一组边重合,
你会得到怎样的图形?
2、这个图形的边有怎样的位置关系?
3、这个图形由哪些部分组成?
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
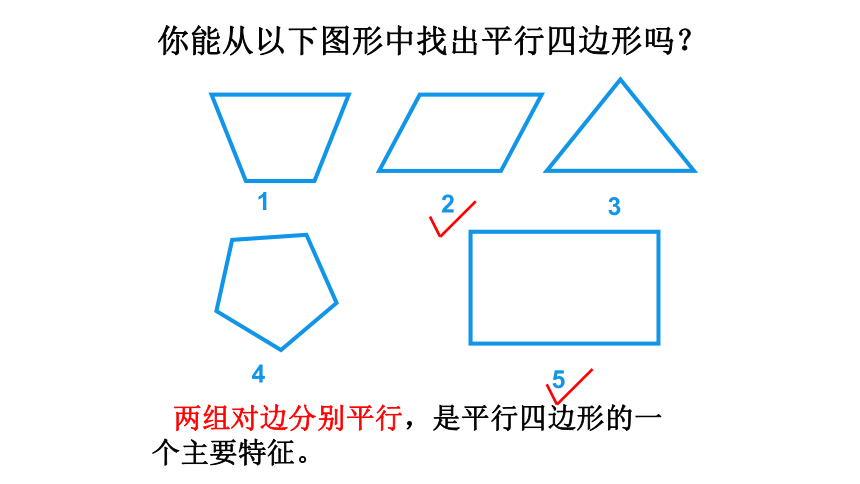
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
2.平行四边形不相邻的两个顶点连成的线段叫平行四 边形的对角线.
1.平行四边形相对的边称为 对边,
相对的角称为 对角.
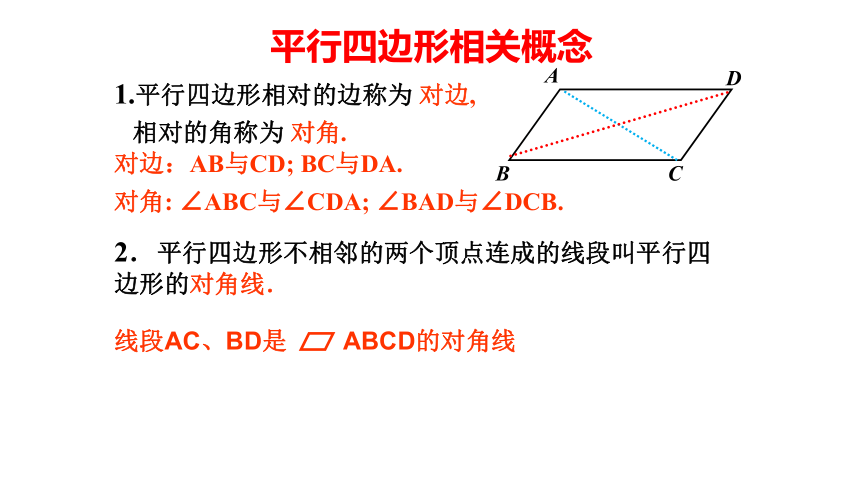
平行四边形相关概念
A
D
C
B
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
线段AC、BD是 ABCD的对角线
自主学习(先自己动手,再小组合作完成下列问题)
AB
CD
AD
BC
∠A
∠B
∠C
∠D
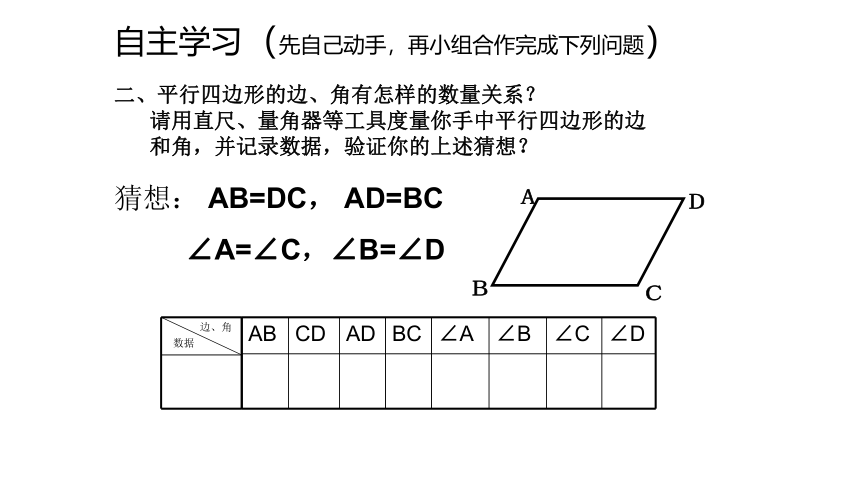
二、平行四边形的边、角有怎样的数量关系?
请用直尺、量角器等工具度量你手中平行四边形的边
和角,并记录数据,验证你的上述猜想?
边、角
数据
猜想: AB=DC, AD=BC
∠A=∠C,∠B=∠D
自主学习(小组合作完成下列问题)
三、用以前所学过的知识能否证明出自己的猜想?
已知:
求证:
,
,
D
C
A
B
,
几何语言:
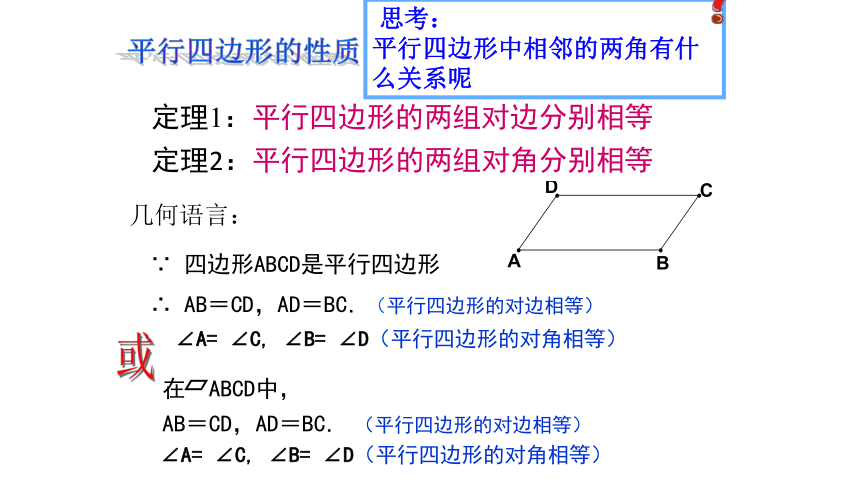
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC. (平行四边形的对边相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
定理2:平行四边形的两组对角分别相等
思考:
平行四边形中相邻的两角有什么关系呢
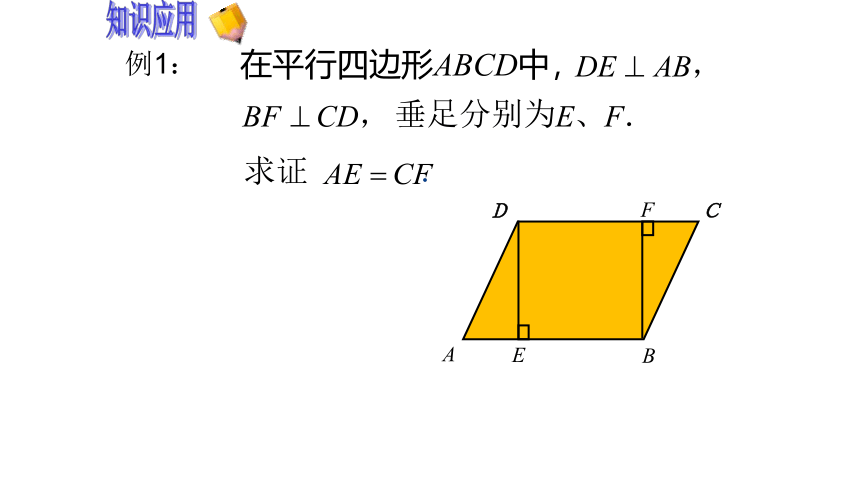
在平行四边形ABCD中,
垂足分别为
求证 .
A
B
D
C
E
F
例1:
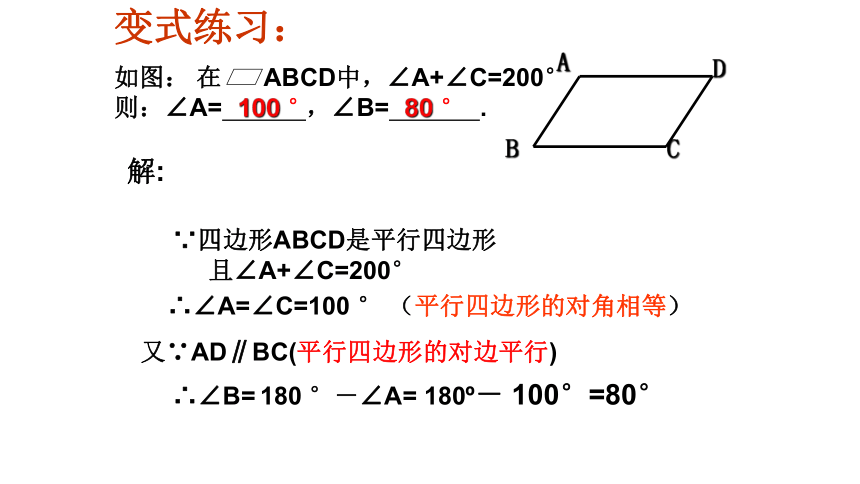
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
变式练习:
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180?- 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
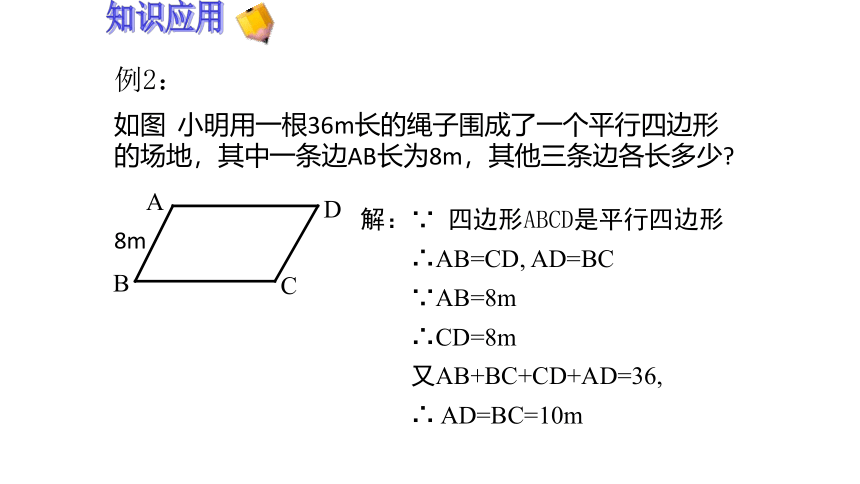
如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
A
D
B
C
8m
例2:
1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。
作业:
必做题 课本43页 1,2
选做题 课本56页 1,3
。
教 材 解 读
学 情 分 析
目 标 定 位
基 本 理 念
1
2
3
4
5
教 学 设 计
一
The teacher open class
教 材 解 读
《平行四边形的性质》是人教版八年级数学第二学期第十八章第一节第一节课内容。
它是在学生掌握了平行线、三角形及简单图形的平移等几何知识的基础上进一步认识学习更复杂的平面几何图形。
学习它不仅是对已学平行线、三角形等知识的综合应用和深化,提升推理探究能力,又是下一步学习矩形、菱形、正方形及梯形等特殊四边形的基础,起着承上启下的作用。
二
The teacher open class
学 情 分 析
学生在小学阶段已对平行四边形有了初步、直观的认识,为平行四边形性质的研究提供了一定的认知基础.
八年级学生正处在试验几何向论证几何的过渡阶段。通过学生动手操作来实现探究活动,进一步调动他们的求知欲。
通过观察、操作、猜想、验证等自主探究活动,让学生经历平行四边形性质的生成过程。通过展示与交流活动实现知识的共享,思维的碰撞,知识的互补,使课堂成为学生自主探索,自我发展,自由成长的舞台。
三
The teacher open class
目 标 定 位
1
1.掌握并理解平行四边形的概念和性质。会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证。
2
3
2.通过观察平行四边形,猜测、证明、归纳平行四边形的性质,能运用几何语言,发展学生合理的推理意识。
3. 在探究平行四边形性质的过程中,培养学生发现问题、解决问题的能力及逻辑推理能力。
透过现象看本质是中考复习中重要的学习的方法,也是中考复习的应该抓住的重点。.
四
The teacher open class
基 本 理 念
以生为本,以教师为主导,学生为主体;渗透转化的数学思想,培养学生学习学生的应用意识和严谨的逻辑推理能力。
五
The teacher open class
教 学 设 计
1
创设情境,引入新课
2
3
qi'f
4
探索新知,获得体验
典型例题,应用理解
练习巩固,内化知识
5
i'f
课堂小结,归纳提升
设计意图:从学生的生活实际出发,创设情境,提出问题。学生经历了讲实际问题抽象为数学问题的建模过程。
1
创设情境,引入新课
设计意图:通过拼图的过程,让学生经历探究图形的形状、大小、位置关系和变换的过程,加强对四边形的认识,通过两个三角形拼接出平行四边形的过程,渗透转化的思想.
2
探索新知,获得体验
设计意图:通过动手测量,感受猜想的乐趣,培养猜想的意识。
3
探索新知,获得体验
设计意图:培养学生互相学习、合作交流的好习惯。通过展示的规范化板书,严密的几何证明, 体会通过添加辅助线将四边形的有关问题转化为三角形的问题,从中体会转化思想。
4
探索新知,获得体验
设计意图:通过例题、练习闯关等活动,使学生达到灵活应用平行四边形性质定理解决相关问题,进一步训练学生的应用意识和严谨的逻辑推理能力。
5
典型例题,应用理解
设计意图:引导学生梳理知识,进一步培养学生的反思意识及总结能力.
6
课堂小结,归纳提升
设计意图:通过对学生进行分层作业的布置,让不同层次的学生有不同的收获。
7
作业
必做题 课本43页 1,2
选做题 课本56页 1,3
谢谢您的聆听!
18.1.1 平行四边形的性质
第1课时
自主学习(先自己动手,再小组合作完成下列问题)
1、将一张纸对折,剪下两个完全一样的三角
形纸片,将这两个三角形相等的一组边重合,
你会得到怎样的图形?
2、这个图形的边有怎样的位置关系?
3、这个图形由哪些部分组成?
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
2.平行四边形不相邻的两个顶点连成的线段叫平行四 边形的对角线.
1.平行四边形相对的边称为 对边,
相对的角称为 对角.
平行四边形相关概念
A
D
C
B
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
线段AC、BD是 ABCD的对角线
自主学习(先自己动手,再小组合作完成下列问题)
AB
CD
AD
BC
∠A
∠B
∠C
∠D
二、平行四边形的边、角有怎样的数量关系?
请用直尺、量角器等工具度量你手中平行四边形的边
和角,并记录数据,验证你的上述猜想?
边、角
数据
猜想: AB=DC, AD=BC
∠A=∠C,∠B=∠D
自主学习(小组合作完成下列问题)
三、用以前所学过的知识能否证明出自己的猜想?
已知:
求证:
,
,
D
C
A
B
,
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC. (平行四边形的对边相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
定理2:平行四边形的两组对角分别相等
思考:
平行四边形中相邻的两角有什么关系呢
在平行四边形ABCD中,
垂足分别为
求证 .
A
B
D
C
E
F
例1:
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
变式练习:
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180?- 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
A
D
B
C
8m
例2:
1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。
作业:
必做题 课本43页 1,2
选做题 课本56页 1,3
。
教 材 解 读
学 情 分 析
目 标 定 位
基 本 理 念
1
2
3
4
5
教 学 设 计
一
The teacher open class
教 材 解 读
《平行四边形的性质》是人教版八年级数学第二学期第十八章第一节第一节课内容。
它是在学生掌握了平行线、三角形及简单图形的平移等几何知识的基础上进一步认识学习更复杂的平面几何图形。
学习它不仅是对已学平行线、三角形等知识的综合应用和深化,提升推理探究能力,又是下一步学习矩形、菱形、正方形及梯形等特殊四边形的基础,起着承上启下的作用。
二
The teacher open class
学 情 分 析
学生在小学阶段已对平行四边形有了初步、直观的认识,为平行四边形性质的研究提供了一定的认知基础.
八年级学生正处在试验几何向论证几何的过渡阶段。通过学生动手操作来实现探究活动,进一步调动他们的求知欲。
通过观察、操作、猜想、验证等自主探究活动,让学生经历平行四边形性质的生成过程。通过展示与交流活动实现知识的共享,思维的碰撞,知识的互补,使课堂成为学生自主探索,自我发展,自由成长的舞台。
三
The teacher open class
目 标 定 位
1
1.掌握并理解平行四边形的概念和性质。会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证。
2
3
2.通过观察平行四边形,猜测、证明、归纳平行四边形的性质,能运用几何语言,发展学生合理的推理意识。
3. 在探究平行四边形性质的过程中,培养学生发现问题、解决问题的能力及逻辑推理能力。
透过现象看本质是中考复习中重要的学习的方法,也是中考复习的应该抓住的重点。.
四
The teacher open class
基 本 理 念
以生为本,以教师为主导,学生为主体;渗透转化的数学思想,培养学生学习学生的应用意识和严谨的逻辑推理能力。
五
The teacher open class
教 学 设 计
1
创设情境,引入新课
2
3
qi'f
4
探索新知,获得体验
典型例题,应用理解
练习巩固,内化知识
5
i'f
课堂小结,归纳提升
设计意图:从学生的生活实际出发,创设情境,提出问题。学生经历了讲实际问题抽象为数学问题的建模过程。
1
创设情境,引入新课
设计意图:通过拼图的过程,让学生经历探究图形的形状、大小、位置关系和变换的过程,加强对四边形的认识,通过两个三角形拼接出平行四边形的过程,渗透转化的思想.
2
探索新知,获得体验
设计意图:通过动手测量,感受猜想的乐趣,培养猜想的意识。
3
探索新知,获得体验
设计意图:培养学生互相学习、合作交流的好习惯。通过展示的规范化板书,严密的几何证明, 体会通过添加辅助线将四边形的有关问题转化为三角形的问题,从中体会转化思想。
4
探索新知,获得体验
设计意图:通过例题、练习闯关等活动,使学生达到灵活应用平行四边形性质定理解决相关问题,进一步训练学生的应用意识和严谨的逻辑推理能力。
5
典型例题,应用理解
设计意图:引导学生梳理知识,进一步培养学生的反思意识及总结能力.
6
课堂小结,归纳提升
设计意图:通过对学生进行分层作业的布置,让不同层次的学生有不同的收获。
7
作业
必做题 课本43页 1,2
选做题 课本56页 1,3
谢谢您的聆听!
