八年级数学下册课件-18.2.1 矩形1-人教版(共24张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.2.1 矩形1-人教版(共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 00:00:00 | ||
图片预览







文档简介
18.2 特殊的平行四边形
18.2.1 矩形
新人教版八年级第十八章
一.复习平行四边形的性质
边
对边相等,对边平行
角
对角相等,邻角互补
对角线
对角线互相平分
(学生回答,多媒体演示)
教学过程
问题一:在拖动过程中,什么在发生变化?
问题二:平行四边形的一个内角由锐角变为钝角的过程中,会发生什么特殊情况?这时的图形是什么图形?
(学生拿出自制平行四边形学具,分组活动)
二、探究新知
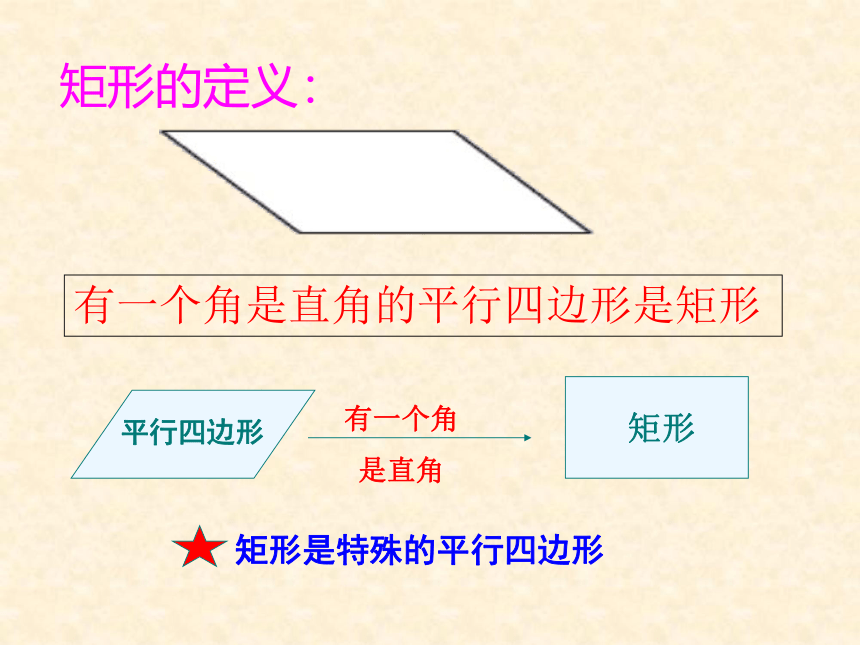
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
联系生活
请同学们举出生活中的矩形实例
五星红旗 电视机面 香港区旗 手表
窗框 书桌面 课本封面 地砖
生活中的矩形:
练兵场:试试你的身手吧,相信自己绝对能行!
(一)请用所学的知识诊断下面的语句,若正确请在括号里打“√” 若“有病”请开药方:
1.矩形是特殊的平行四边形,特殊之处就是有一个角是直角.( )
2.平行四边形是矩形. ( )
3.平行四边形具有的性质(如平行四边形的对边平行且相等;平行四边形的对角相等;平行四边形的对角线互相平分.) 矩形也具有. ( )
√
√
?
有一个角是直角的平行四边形是直角
具备平行四边形所有的性质
矩形的一般性质:
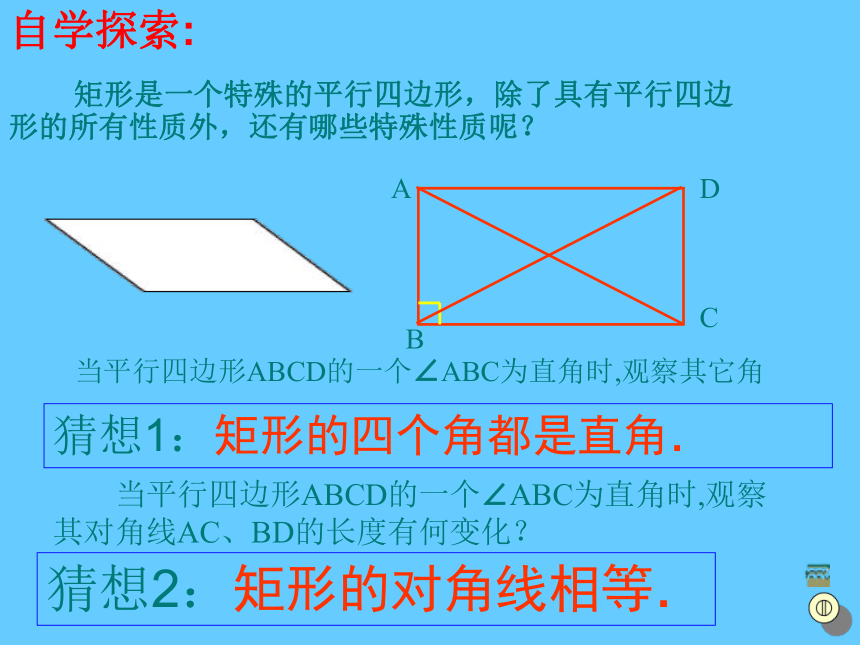
自学探索:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
当平行四边形ABCD的一个∠ABC为直角时,观察其它角
当平行四边形ABCD的一个∠ABC为直角时,观察其对角线AC、BD的长度有何变化?
B
A
D
C
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B =180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
矩形的特殊性质
矩形的对角线相等
数学语言
∵四边形ABCD是矩形
∴AC = BD
A
B
C
D
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等,
从角上看:
从对角线上看:
且互相平分。
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
A
B
C
D
O
得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
在Rt△ABC中, BO= AC
探索新知
在直角三角形ABC中,O是AC中点,思考BO与AC的数量关系
D
B
D
C
A
O
A
C
B
O
D
C
B
A
┓
4.已知Rt△ ABC中,∠ABC=900,
BD是斜边AC上的中线
(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.
6
5
10
绝招巧试
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形.
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
解:∵ 四边形ABCD是矩形
D
C
B
A
o
勇士闯关训练营
点击进入
矩形具有而一般平行四边形不
具有的性质是 ( )
B.对边相等
A.对角相等
C.对角线相等
D.对角线互相平分
C
营中热身
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
营中寻宝
本课小结
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
矩形是轴对称图形
100
作 业
恭喜你,全面掌握了这节课的内容!
1. P53练习第2题
2. P60 习题18.2 第4题。
再见
18.2.1 矩形
新人教版八年级第十八章
一.复习平行四边形的性质
边
对边相等,对边平行
角
对角相等,邻角互补
对角线
对角线互相平分
(学生回答,多媒体演示)
教学过程
问题一:在拖动过程中,什么在发生变化?
问题二:平行四边形的一个内角由锐角变为钝角的过程中,会发生什么特殊情况?这时的图形是什么图形?
(学生拿出自制平行四边形学具,分组活动)
二、探究新知
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
联系生活
请同学们举出生活中的矩形实例
五星红旗 电视机面 香港区旗 手表
窗框 书桌面 课本封面 地砖
生活中的矩形:
练兵场:试试你的身手吧,相信自己绝对能行!
(一)请用所学的知识诊断下面的语句,若正确请在括号里打“√” 若“有病”请开药方:
1.矩形是特殊的平行四边形,特殊之处就是有一个角是直角.( )
2.平行四边形是矩形. ( )
3.平行四边形具有的性质(如平行四边形的对边平行且相等;平行四边形的对角相等;平行四边形的对角线互相平分.) 矩形也具有. ( )
√
√
?
有一个角是直角的平行四边形是直角
具备平行四边形所有的性质
矩形的一般性质:
自学探索:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
当平行四边形ABCD的一个∠ABC为直角时,观察其它角
当平行四边形ABCD的一个∠ABC为直角时,观察其对角线AC、BD的长度有何变化?
B
A
D
C
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B =180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
矩形的特殊性质
矩形的对角线相等
数学语言
∵四边形ABCD是矩形
∴AC = BD
A
B
C
D
矩形特殊的性质
矩形的四个角都是直角.
矩形的两条对角线相等,
从角上看:
从对角线上看:
且互相平分。
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
A
B
C
D
O
得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
在Rt△ABC中, BO= AC
探索新知
在直角三角形ABC中,O是AC中点,思考BO与AC的数量关系
D
B
D
C
A
O
A
C
B
O
D
C
B
A
┓
4.已知Rt△ ABC中,∠ABC=900,
BD是斜边AC上的中线
(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.
6
5
10
绝招巧试
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形.
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
解:∵ 四边形ABCD是矩形
D
C
B
A
o
勇士闯关训练营
点击进入
矩形具有而一般平行四边形不
具有的性质是 ( )
B.对边相等
A.对角相等
C.对角线相等
D.对角线互相平分
C
营中热身
已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
营中寻宝
本课小结
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
矩形是轴对称图形
100
作 业
恭喜你,全面掌握了这节课的内容!
1. P53练习第2题
2. P60 习题18.2 第4题。
再见
