八年级数学下册课件-18.2.1 矩形3-人教版(共29张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.2.1 矩形3-人教版(共29张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 19:05:42 | ||
图片预览





文档简介
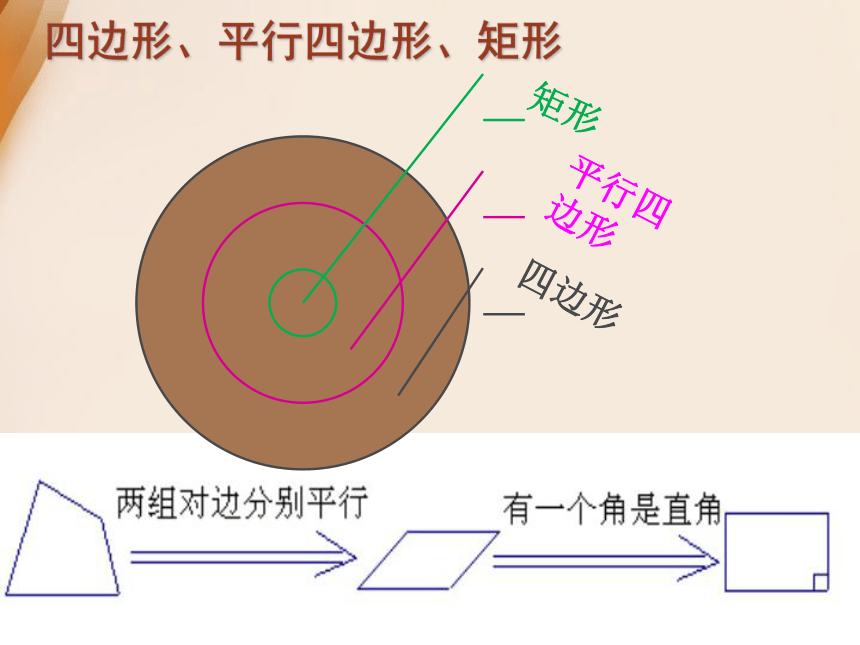
特殊的平行四边形
两组对边
分别平行
平行
四边形
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质。
同样对于平行四边形来说也有特殊情况,这堂课我们就来研究一种特殊的平行四边形————————
矩形
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
矩形的定义
四边形、平行四边形、矩形
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
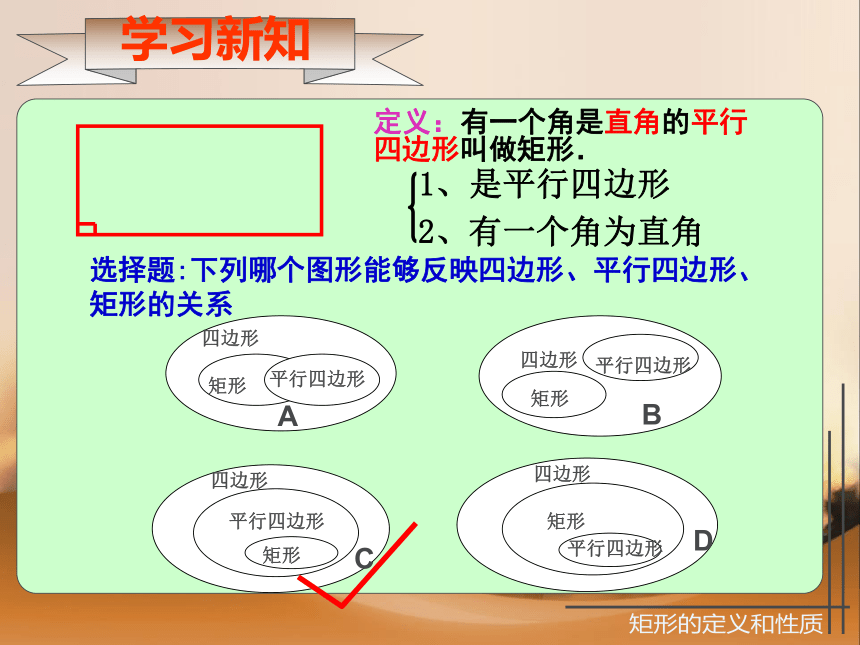
定义:有一个角是直角的平行四边形叫做矩形.
1、是平行四边形
2、有一个角为直角
选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
矩形的定义和性质
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
D
C
学习新知
矩形的性质的探究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有其它的特殊性质.你能说出矩形有哪些特殊性质吗?
四、矩形 两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
五、矩形的邻角互补
请同学们用量角器度量你的课本每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想.
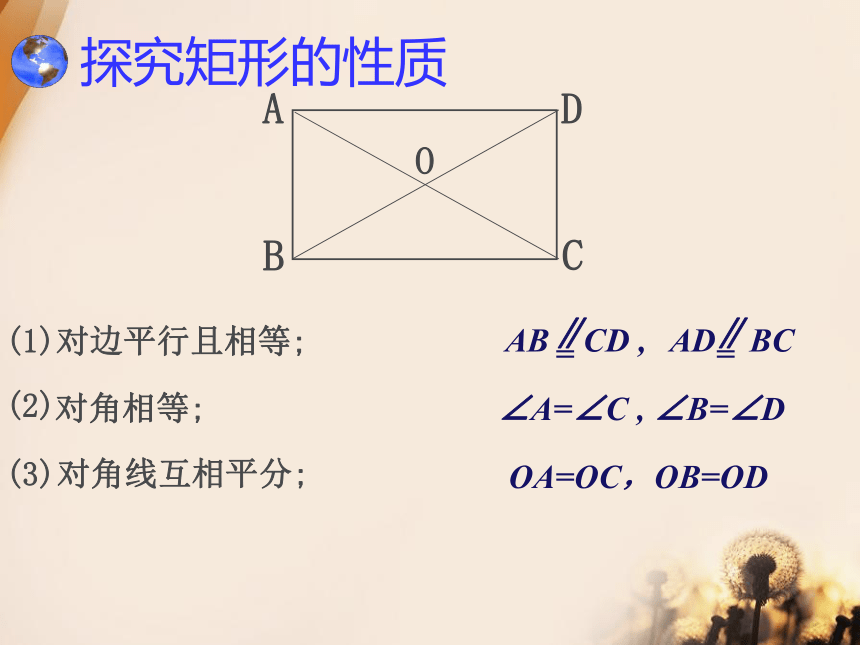
探究矩形的性质
A
C
B
D
O
(1)对边平行且相等;
(2)
(3)
AB CD ,
=
∥
AD BC
=
∥
∠A=∠C , ∠B=∠D
OA=OC,OB=OD
对角相等;
对角线互相平分;
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
矩形是轴对称图形.
A
B
C
D
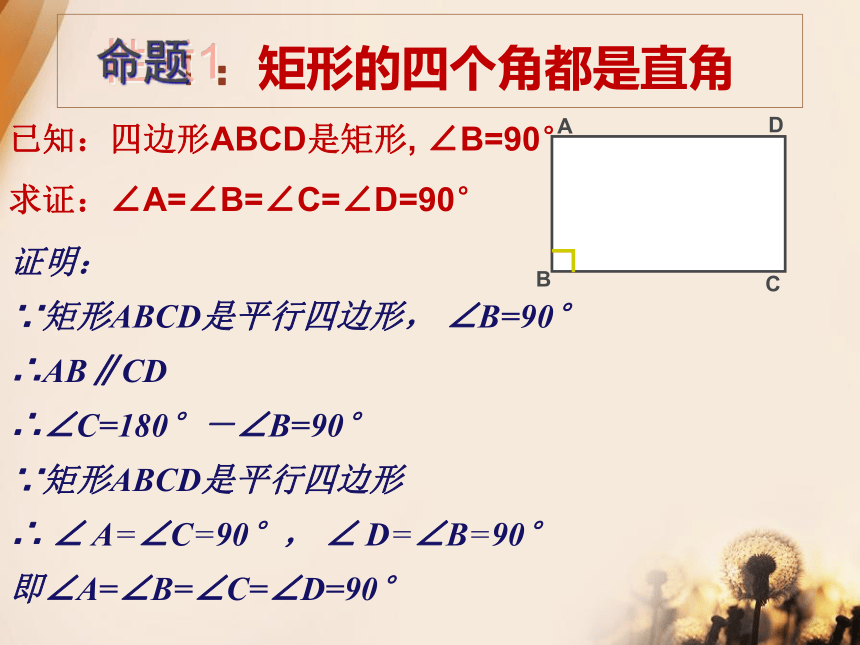
1:矩形的四个角都是直角
已知:四边形ABCD是矩形, ∠B=90°
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:
∵矩形ABCD是平行四边形, ∠B=90°
∴AB∥CD
∴∠C=180°-∠B=90°
∵矩形ABCD是平行四边形
∴ ∠ A=∠C=90°, ∠ D=∠B=90°
即∠A=∠B=∠C=∠D=90°
性质1
命题
已知:四边形ABCD是矩形,求证:AC = BD
A
B
C
D
证明:
在矩形ABCD中,
有∠ABC = ∠DCB = 90°, AB = DC
∵ AB = DC
∠ABC = ∠DCB = 90°
BC = CB
∴△ABC≌△DCB
∴AC = BD
2:矩形的对角线相等.
性质
命题
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
数学几何语言
∵四边形ABCD是矩形
∴AD = BC ,CD = AB
∴AD∥ BC ,CD∥ AB
∴AC= BD
A
B
C
D
O
∴OA= OC ,OD = OB
矩形的性质
OA=OC,OB=OD
OA=OC=OB=OD
∠BAD=∠BCD =∠ABC=∠ADC= 90°
探究矩形的性质
A
C
B
D
O
(1)对边平行且相等;
(2)
(3)
AB CD ,
=
∥
AD BC
=
∥
∠A=∠C , ∠B=∠D
矩形的四个角都是直角;
矩形的对角线相等
对角相等;
对角线互相平分;
且互相平分;
1.矩形具有而一般平行四边形不
具有的性质是 ( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
小试身手
2.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形。
(A)2 (B)4
(C)6 (D)8
B
3.如果矩形的一个内角平分线将它的一边分成3cm和5cm两部分,则它的面积是多少?
A
B
C
D
E
A
B
C
D
E
3
5
3
5
小试身手
3
5
面积是:24或
40
已知:四边形ABCD是矩形
(1)若AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
典例赏析
∵矩形ABCD中,有∠DAB=90°
∴在Rt△ABD中,BD=AB????+AD????
=????????+????????
=10cm
?
∴矩形ABCD中,AC=BD=10cm,
OB=????????BD=5cm
?
10
5
解:
O
D
C
B
A
四边形ABCD是矩形
2.若已知AC=13㎝,BC=5㎝,则矩形的周长=____ cm
矩形的面积=_______ ㎝2
34
60
∵矩形ABCD中,有∠ABC=90°
∴在Rt△ABC中,AB=A????????-BC????
=????????????-????????
=12cm
?
∵矩形ABCD中,有AD=BC=5cm,CD=AB=12cm
∴矩形ABCD的周长为:12+5+12+5=34cm,
面积为:12×5=60cm2
典例赏析
解:
O
D
C
B
A
四边形ABCD是矩形
3. 若已知 ∠DOC=120°,AD=7㎝,则AC= _____cm
O
D
C
B
A
14
∵矩形ABCD中,有AC=BD,
OA=????????AC,OD=????????BD
?
∴OA=OD
又∵∠1=
1
180°-∠DOC
=180°-120°
=60°
∴△AOD为等边三角形,OA=AD=7 cm
∴矩形ABCD中,有AC=2OA=14 cm
典例赏析
解:
四边形ABCD是矩形
3. 若已知 ∠DOC=120°,AD=7㎝,则AC= _____cm
O
D
C
B
A
14
∵矩形ABCD中,有AC=BD,
OC=????????AC,OD=????????BD
?
∴OC=OD
∴∠1=∠2=
1
????????(180°-∠DOC)=30°
?
∴在Rt△ADC中,AC=2AD=14 cm
又∵矩形ABCD中,有∠ADC=90°
典例赏析
解:
2
1、矩形的两条边长是6、8,则矩形的对角线长是_________
2、一矩形的周长是24cm,相邻两边之比是1:3,那么这个矩形的面积是__________
3、矩形的一条对角线与一边的夹角是35°,则对角线相交所成的锐角是____________
4、矩形中较短的边长为3.6cm,两条对角线相交的锐角为60°,则矩形对角线的长度是___________
5、矩形的边长是45cm和20cm,其中一个内角的平分线分较长边为两部分,这两部分长分别是___________
10
过关练习
27 cm2
70°
7.2 cm
20cm和25cm
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
小明
小亮
新民学校在建设绿色校园的过程中修建了一块长8米,宽6米的矩形绿草地,为方便师生参观,沿对角线修筑了一条卵石小道.但是……唉!
8米
6米
A
B
C
D
O
生活链接---芳草的哭泣
O
D
C
B
A
┛
在矩形ABCD中,
OA=OC= AC= BD= OB=OD
∵在Rt△ABD中,OA是斜边BD上的中线
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半。
你能从中得出直角三角形
的性质吗?
∴OA= ?????????BD=OB=OD
?
D
C
B
A
┓
已知△ABC是直角三角形,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝, ∠BDC= °
6
5
10
小试身手
(3)若∠C=30°,
判断△ABD形状:
判断△CBD形状:
120
等边三角形
等腰三角形
已知:如图BE、CF是△ABC的两条高,M为BC的中点,分别连ME、MF.求证:
(1)ME= ????????BC
(2)ME=MF
(3)连接EF,N是EF中点,试猜测MN与EF的关系,并说明理由.
?
C
M
A
B
F
E
典例赏析
N
1.如图 ,四边形ABCD中,∠ABC=∠ADC=90°,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。
A
B
C
D
E
F
过关练习
┓
H
E
F
D
C
B
A
2.如图,在△ABC中,D、E、F分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=
8㎝
小试身手
我成长,我快乐,我收获
矩形的四个角都是直角.
※ 矩形的性质1
矩形的对角线相等.
※ 矩形的性质2
※ 直角三角形性质
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
6.矩形ABCD中,AB= 4,BC=2,E是边CD上的一点,AE=AB.求∠BEC的度数.
A
B
C
D
E
过关练习
1.为了庆祝五一劳动节,新民学校八年级(13)班同学要在广场上布置一个矩形的花坛,计划用“串红”摆成两条对角线,如果一条对角线用了38盆“串红”,还需要从花房里运来多少盆“串红”?为什么?如果一条对角线用了49盆呢?为什么?
生活链接
两组对边
分别平行
平行
四边形
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质。
同样对于平行四边形来说也有特殊情况,这堂课我们就来研究一种特殊的平行四边形————————
矩形
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
矩形的定义
四边形、平行四边形、矩形
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
定义:有一个角是直角的平行四边形叫做矩形.
1、是平行四边形
2、有一个角为直角
选择题:下列哪个图形能够反映四边形、平行四边形、
矩形的关系
矩形的定义和性质
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
D
C
学习新知
矩形的性质的探究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有其它的特殊性质.你能说出矩形有哪些特殊性质吗?
四、矩形 两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
五、矩形的邻角互补
请同学们用量角器度量你的课本每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想.
探究矩形的性质
A
C
B
D
O
(1)对边平行且相等;
(2)
(3)
AB CD ,
=
∥
AD BC
=
∥
∠A=∠C , ∠B=∠D
OA=OC,OB=OD
对角相等;
对角线互相平分;
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
矩形是轴对称图形.
A
B
C
D
1:矩形的四个角都是直角
已知:四边形ABCD是矩形, ∠B=90°
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:
∵矩形ABCD是平行四边形, ∠B=90°
∴AB∥CD
∴∠C=180°-∠B=90°
∵矩形ABCD是平行四边形
∴ ∠ A=∠C=90°, ∠ D=∠B=90°
即∠A=∠B=∠C=∠D=90°
性质1
命题
已知:四边形ABCD是矩形,求证:AC = BD
A
B
C
D
证明:
在矩形ABCD中,
有∠ABC = ∠DCB = 90°, AB = DC
∵ AB = DC
∠ABC = ∠DCB = 90°
BC = CB
∴△ABC≌△DCB
∴AC = BD
2:矩形的对角线相等.
性质
命题
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
数学几何语言
∵四边形ABCD是矩形
∴AD = BC ,CD = AB
∴AD∥ BC ,CD∥ AB
∴AC= BD
A
B
C
D
O
∴OA= OC ,OD = OB
矩形的性质
OA=OC,OB=OD
OA=OC=OB=OD
∠BAD=∠BCD =∠ABC=∠ADC= 90°
探究矩形的性质
A
C
B
D
O
(1)对边平行且相等;
(2)
(3)
AB CD ,
=
∥
AD BC
=
∥
∠A=∠C , ∠B=∠D
矩形的四个角都是直角;
矩形的对角线相等
对角相等;
对角线互相平分;
且互相平分;
1.矩形具有而一般平行四边形不
具有的性质是 ( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
小试身手
2.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形。
(A)2 (B)4
(C)6 (D)8
B
3.如果矩形的一个内角平分线将它的一边分成3cm和5cm两部分,则它的面积是多少?
A
B
C
D
E
A
B
C
D
E
3
5
3
5
小试身手
3
5
面积是:24或
40
已知:四边形ABCD是矩形
(1)若AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
典例赏析
∵矩形ABCD中,有∠DAB=90°
∴在Rt△ABD中,BD=AB????+AD????
=????????+????????
=10cm
?
∴矩形ABCD中,AC=BD=10cm,
OB=????????BD=5cm
?
10
5
解:
O
D
C
B
A
四边形ABCD是矩形
2.若已知AC=13㎝,BC=5㎝,则矩形的周长=____ cm
矩形的面积=_______ ㎝2
34
60
∵矩形ABCD中,有∠ABC=90°
∴在Rt△ABC中,AB=A????????-BC????
=????????????-????????
=12cm
?
∵矩形ABCD中,有AD=BC=5cm,CD=AB=12cm
∴矩形ABCD的周长为:12+5+12+5=34cm,
面积为:12×5=60cm2
典例赏析
解:
O
D
C
B
A
四边形ABCD是矩形
3. 若已知 ∠DOC=120°,AD=7㎝,则AC= _____cm
O
D
C
B
A
14
∵矩形ABCD中,有AC=BD,
OA=????????AC,OD=????????BD
?
∴OA=OD
又∵∠1=
1
180°-∠DOC
=180°-120°
=60°
∴△AOD为等边三角形,OA=AD=7 cm
∴矩形ABCD中,有AC=2OA=14 cm
典例赏析
解:
四边形ABCD是矩形
3. 若已知 ∠DOC=120°,AD=7㎝,则AC= _____cm
O
D
C
B
A
14
∵矩形ABCD中,有AC=BD,
OC=????????AC,OD=????????BD
?
∴OC=OD
∴∠1=∠2=
1
????????(180°-∠DOC)=30°
?
∴在Rt△ADC中,AC=2AD=14 cm
又∵矩形ABCD中,有∠ADC=90°
典例赏析
解:
2
1、矩形的两条边长是6、8,则矩形的对角线长是_________
2、一矩形的周长是24cm,相邻两边之比是1:3,那么这个矩形的面积是__________
3、矩形的一条对角线与一边的夹角是35°,则对角线相交所成的锐角是____________
4、矩形中较短的边长为3.6cm,两条对角线相交的锐角为60°,则矩形对角线的长度是___________
5、矩形的边长是45cm和20cm,其中一个内角的平分线分较长边为两部分,这两部分长分别是___________
10
过关练习
27 cm2
70°
7.2 cm
20cm和25cm
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
小明
小亮
新民学校在建设绿色校园的过程中修建了一块长8米,宽6米的矩形绿草地,为方便师生参观,沿对角线修筑了一条卵石小道.但是……唉!
8米
6米
A
B
C
D
O
生活链接---芳草的哭泣
O
D
C
B
A
┛
在矩形ABCD中,
OA=OC= AC= BD= OB=OD
∵在Rt△ABD中,OA是斜边BD上的中线
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半。
你能从中得出直角三角形
的性质吗?
∴OA= ?????????BD=OB=OD
?
D
C
B
A
┓
已知△ABC是直角三角形,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝, ∠BDC= °
6
5
10
小试身手
(3)若∠C=30°,
判断△ABD形状:
判断△CBD形状:
120
等边三角形
等腰三角形
已知:如图BE、CF是△ABC的两条高,M为BC的中点,分别连ME、MF.求证:
(1)ME= ????????BC
(2)ME=MF
(3)连接EF,N是EF中点,试猜测MN与EF的关系,并说明理由.
?
C
M
A
B
F
E
典例赏析
N
1.如图 ,四边形ABCD中,∠ABC=∠ADC=90°,E是AC中点,EF平分∠BED交BD于点F,
(1)猜想EF与BD具有怎样的关系?
(2)试证明你的猜想。
A
B
C
D
E
F
过关练习
┓
H
E
F
D
C
B
A
2.如图,在△ABC中,D、E、F分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=
8㎝
小试身手
我成长,我快乐,我收获
矩形的四个角都是直角.
※ 矩形的性质1
矩形的对角线相等.
※ 矩形的性质2
※ 直角三角形性质
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
6.矩形ABCD中,AB= 4,BC=2,E是边CD上的一点,AE=AB.求∠BEC的度数.
A
B
C
D
E
过关练习
1.为了庆祝五一劳动节,新民学校八年级(13)班同学要在广场上布置一个矩形的花坛,计划用“串红”摆成两条对角线,如果一条对角线用了38盆“串红”,还需要从花房里运来多少盆“串红”?为什么?如果一条对角线用了49盆呢?为什么?
生活链接
