八年级数学下册课件-18.2.2 菱形69-人教版(共16张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.2.2 菱形69-人教版(共16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 630.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-05 18:59:22 | ||
图片预览




文档简介
八 年 级 下 册 第 十 八 章平 行 四 边 形
想一想:
1.菱形、矩形的定义?
2.它们分别比平行四边形多了哪些性质?
3.怎样判定一个四边形是矩形?
前置性作业:
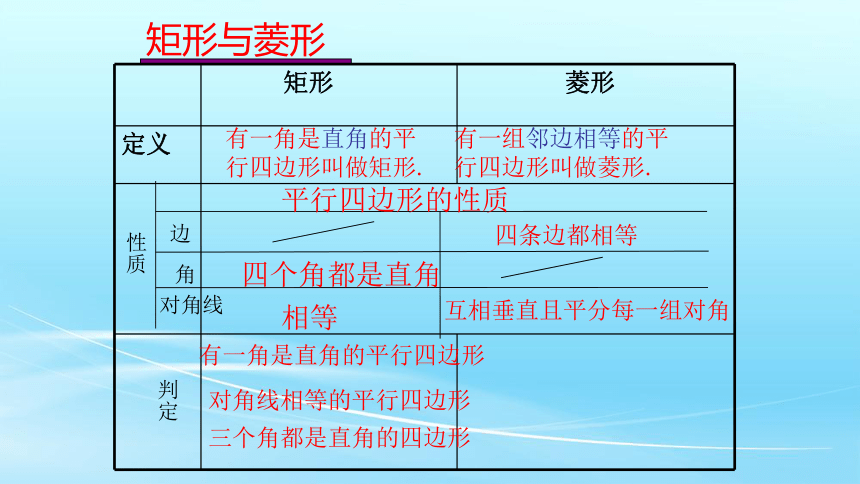
矩形与菱形
矩形
菱形
定义
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
平行四边形的性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
四条边都相等
1.掌握菱形的三种判定方法,能根据不同的已知条件,选择适当的判定定理进行推理和计算;
2.经历菱形判定定理的探究过程,渗透类比思想,体会研究图形判定的一般思路.
学习目标:
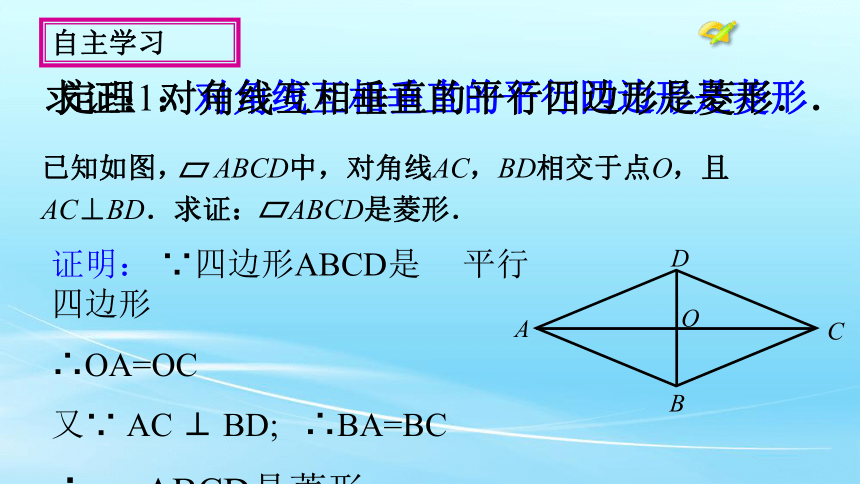
定理1:对角线互相垂直的平行四边形是菱形.
自主学习
求证:对角线互相垂直的平行四边形是菱形.
已知如图, ABCD中,对角线AC,BD相交于点O,且
AC⊥BD.求证: ABCD是菱形.
B
C
A
D
O
证明: ∵四边形ABCD是 平行四边形
∴OA=OC
又∵ AC ⊥ BD; ∴BA=BC
∴ ABCD是菱形
自主学习
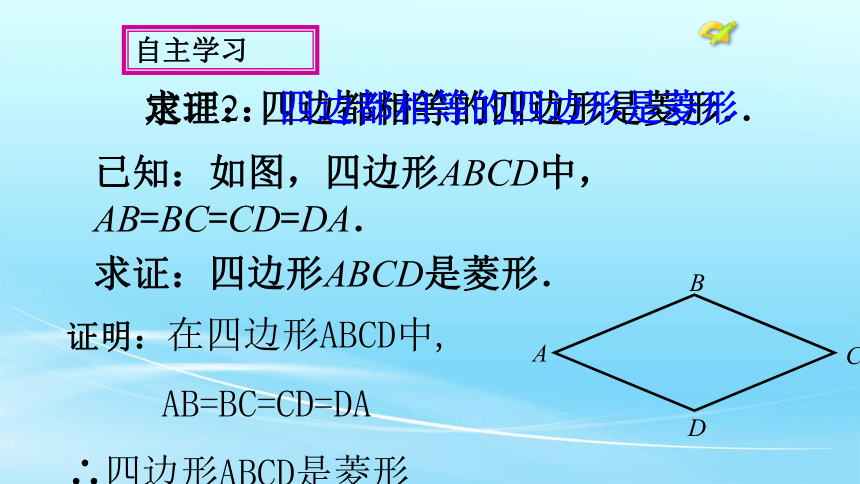
求证:四边都相等的四边形是菱形.
已知:如图,四边形ABCD中, AB=BC=CD=DA.
求证:四边形ABCD是菱形.
D
C
A
B
定理2:四边都相等的四边形是菱形.
证明:在四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形
归纳
菱形常用的判定方法:
1.有一组邻边相等的平行四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
3.有四条边相等的四边形是菱形.
1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。
A
B
C
D
E
F
合作研讨
1.如图,□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
菱
矩
矩
菱
2.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
3.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对
C
4.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
c
A
B
C
D
O
E
5.已知:如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
思考:
一组邻边相等
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
小结:
课后作业
作业:
1.教科书第58页练习第1,2,3题;
2.习题18.2第6,10题.
想一想:
1.菱形、矩形的定义?
2.它们分别比平行四边形多了哪些性质?
3.怎样判定一个四边形是矩形?
前置性作业:
矩形与菱形
矩形
菱形
定义
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
平行四边形的性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
四条边都相等
1.掌握菱形的三种判定方法,能根据不同的已知条件,选择适当的判定定理进行推理和计算;
2.经历菱形判定定理的探究过程,渗透类比思想,体会研究图形判定的一般思路.
学习目标:
定理1:对角线互相垂直的平行四边形是菱形.
自主学习
求证:对角线互相垂直的平行四边形是菱形.
已知如图, ABCD中,对角线AC,BD相交于点O,且
AC⊥BD.求证: ABCD是菱形.
B
C
A
D
O
证明: ∵四边形ABCD是 平行四边形
∴OA=OC
又∵ AC ⊥ BD; ∴BA=BC
∴ ABCD是菱形
自主学习
求证:四边都相等的四边形是菱形.
已知:如图,四边形ABCD中, AB=BC=CD=DA.
求证:四边形ABCD是菱形.
D
C
A
B
定理2:四边都相等的四边形是菱形.
证明:在四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形
归纳
菱形常用的判定方法:
1.有一组邻边相等的平行四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
3.有四条边相等的四边形是菱形.
1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
如图,Rt△ABC中,∠ACB=900,∠BAC=600,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE,求证:四边形ACEF是菱形。
A
B
C
D
E
F
合作研讨
1.如图,□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
菱
矩
矩
菱
2.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
3.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对
C
4.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分
B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD
D.AB=CD,AD=BC,AC⊥BD
c
A
B
C
D
O
E
5.已知:如图,矩形ABCD的对角线相交于点O,DE∥AC,CE ∥BD.
求证:四边形OCED是菱形
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
思考:
一组邻边相等
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
小结:
课后作业
作业:
1.教科书第58页练习第1,2,3题;
2.习题18.2第6,10题.
